本文主要是介绍计算散点的凸包(格雷厄姆扫描算法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1、概念
在二维平面上,凸包(Convex Hull)就是将最外层的点连接起来构成的凸多边型,它能包含点集中所有的点,可以想象为一
条刚好包著所有点的橡皮圈,空间分析有时也会用到凸包。
下图展示了格雷厄姆扫描算法的过程,图片来源(侵权删除) https://blog.csdn.net/qq_39826163/article/details/83861353

2、查找过程
1、找到y值最小的点p0,保存p0,把p0从集合中移除。
2、把集合中的剩余点按照 和p0的连线 与x轴的角度大小 由小到大排序
3、把p0和角度最小的点p1加入结果集中(p0,p1和角度最大的点肯定在结果集中,先加入p0、p1,迭代时再加入p8),
把p2加入结果集(在后面的循环过程汇总根据是否符合条件,再去除结果集中最后的点)。
4、循环集合中的点,如果集合中的点在结果集中最后两点的右侧,就移除结果集中的最后的点(移除后再迭代判断结果
集中的最后两点和当前循环点的左右关系,在右侧就移除结果集中的最后的点(迭代删除结果集中的点),在左侧就
不必删除,直接),加入当前循环点。
点和直线的左右关系,请参考:https://blog.csdn.net/shijie_nihao/article/details/99566466
5、集合循环完毕,结果集 就是所有“凸点”了
3、计算效果
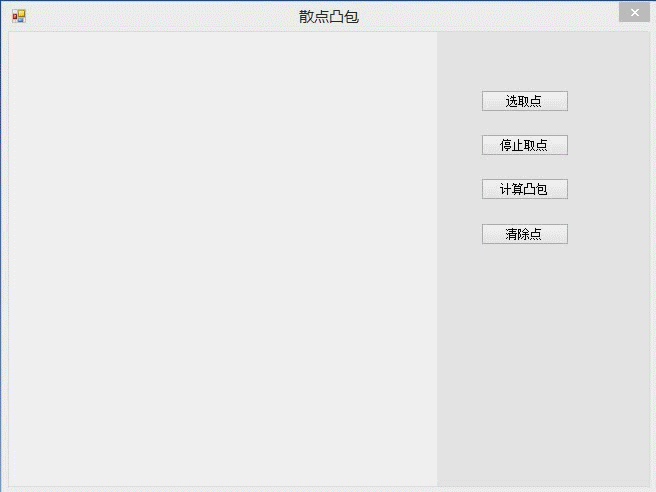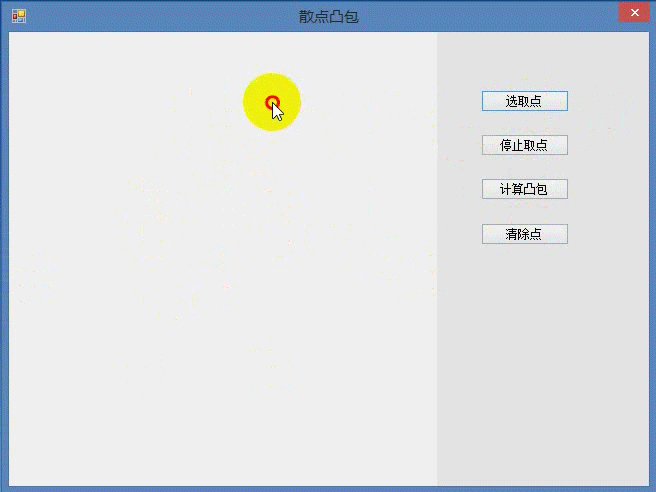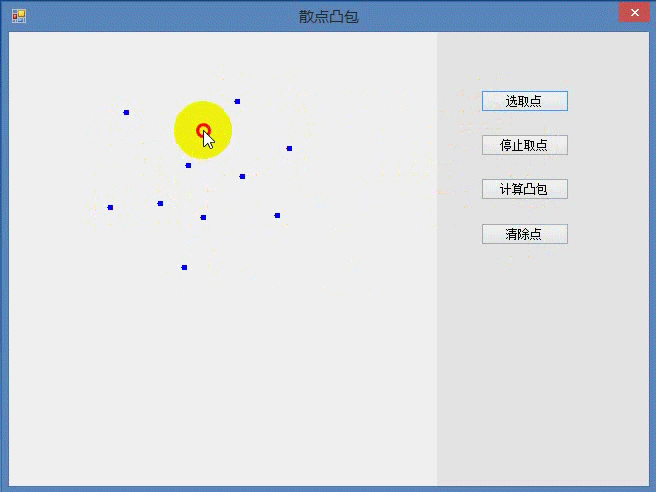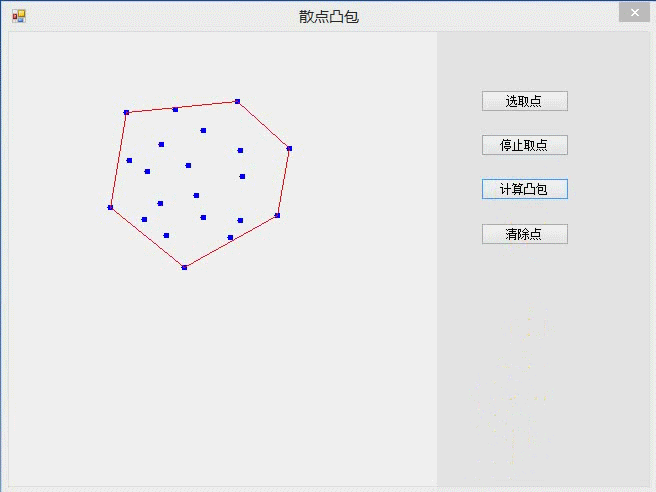
代码下载:https://download.csdn.net/download/shijie_nihao/11545918
这篇关于计算散点的凸包(格雷厄姆扫描算法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




