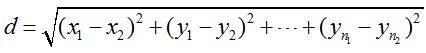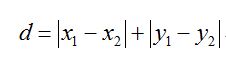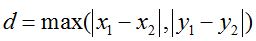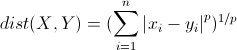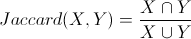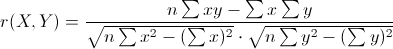18种和“距离(distance)”、“相似度(similarity)”相关的量的小结

摘要：

　　1.常见的距离算法

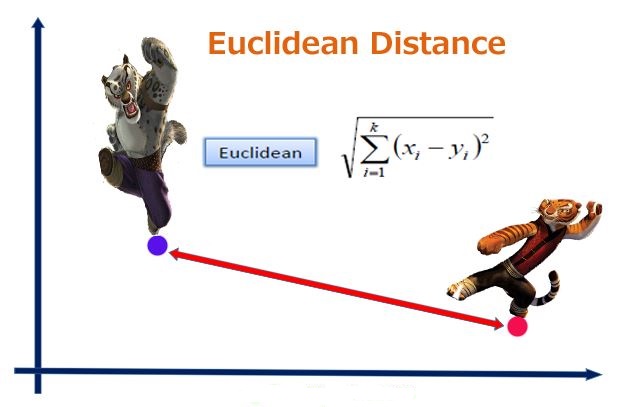
　　　　1.1欧几里得距离（Euclidean Distance）以及欧式距离的标准化（Standardized Euclidean distance）

　　　　1.2马哈拉诺比斯距离（Mahalanobis Distance）

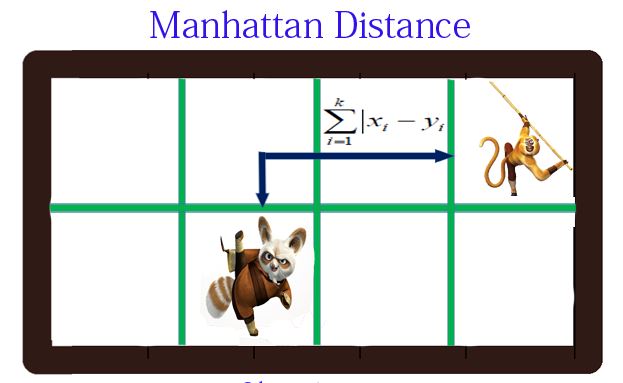
　　　　1.3曼哈顿距离（Manhattan Distance）

　　　　1.4切比雪夫距离（Chebyshev Distance）

　　　　1.5明可夫斯基距离（Minkowski Distance）

　　　　1.6海明距离（Hamming distance）

　　 2.常见的相似度（系数）算法

　　　　2.1余弦相似度（Cosine Similarity）以及调整余弦相似度（Adjusted Cosine Similarity）

　　　　2.2皮尔森相关系数（Pearson Correlation Coefficient）

　　　　2.3Jaccard相似系数（Jaccard Coefficient）

　　　　2.4Tanimoto系数（广义Jaccard相似系数）

　　　　2.5对数似然相似度/对数似然相似率

　　　　2.6互信息/信息增益，相对熵/KL散度

　　　　2.7信息检索--词频-逆文档频率（TF-IDF）

　　　　2.8词对相似度--点间互信息

　　3.距离算法与相似度算法的选择（对比）

内容：

　　1.常见的距离算法

　　　　1.1欧几里得距离（Euclidean Distance）

　　　　公式：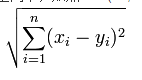

　　　　标准欧氏距离的思路：现将各个维度的数据进行标准化：标准化后的值 = ( 标准化前的值 － 分量的均值 ) /分量的标准差，然后计算欧式距离

　　　　欧式距离的标准化（Standardized Euclidean distance）

　　　　公式：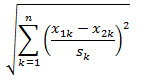

　　　　1.2马哈拉诺比斯距离（Mahalanobis Distance）

　　　　公式：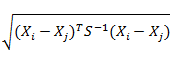

 　　　 关系：若协方差矩阵是对角矩阵，公式变成了标准化欧氏距离；如果去掉马氏距离中的协方差矩阵，就退化为欧氏距离。欧式距离就好比一个参照值，它表征的是当所有类别等概率出现的情况下，类别之间的距离；当类别先验概率并不相等时，马氏距离中引入的协方差参数（表征的是点的稀密程度）来平衡两个类别的概率。

　　　  特点：量纲无关，排除变量之间的相关性的干扰。 

　        扩展

　　　　1.3曼哈顿距离（Manhattan Distance）

　　　　公式：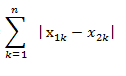

 　　　　定义：通俗来讲，想象你在曼哈顿要从一个十字路口开车到另外一个十字路口实际驾驶距离就是这个“曼哈顿距离”，此即曼哈顿距离名称的来源，同时，曼哈顿距离也称为城市街区距离(City Block distance)。

　　　　1.4切比雪夫距离（Chebyshev Distance）

　　　　公式：

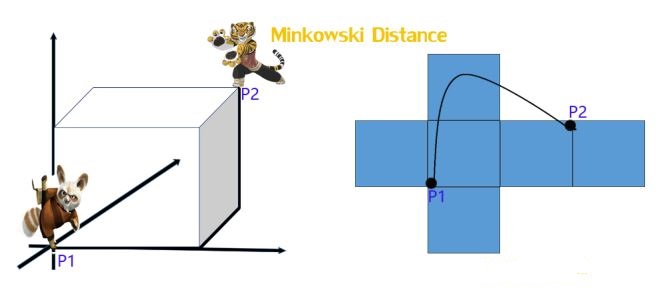
　　　　1.5明可夫斯基距离（Minkowski Distance）

　　　　定义：

　　　　关系：明氏距离是欧氏距离的推广，是对多个距离度量公式的概括性的表述。p=1退化为曼哈顿距离；p=2退化为欧氏距离；切比雪夫距离是明氏距离取极限的形式。这里明可夫斯基距离就是p-norm范数的一般化定义。

　　　  下图给出了一个Lp球（||X||p=1）的形状随着P的减少的可视化图：

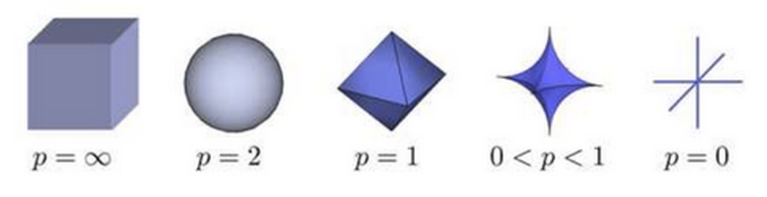
　　　　　　参照：浅谈L0,L1,L2范数及其应用；机器学习中的范数与距离；浅谈压缩感知（十）：范数与稀疏性

　　　　1.6海明距离（Hamming distance）

　　　　定义：在信息论中，两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。

　　　　场景：在海量物品的相似度计算中可用simHash对物品压缩成字符串，然后使用海明距离计算物品间的距离 

　　　　参考simHash 简介以及 java 实现；相似度计算常用方法综述；通过simHash判断数组内容相同（或者网页排重）的测试代码

　　2.常见的相似度（系数）算法

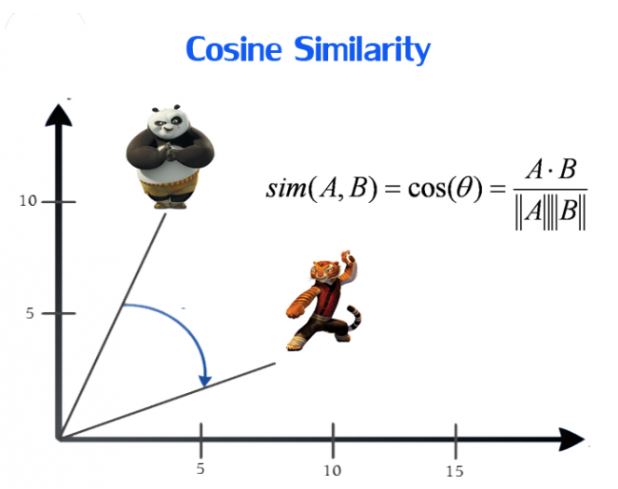
　　　　2.1余弦相似度（Cosine Similarity）

　　　　公式：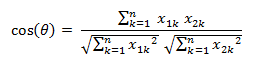

　　　　定义：两向量越相似，向量夹角越小，cosine绝对值越大；值为负，两向量负相关。

　　　　不足：只能分辨个体在维之间的差异，没法衡量每个维数值的差异（比如用户对内容评分，5分制，X和Y两个用户对两个内容的评分分别为（1，2）和（4，5），使用余弦相似度得出的结果是0.98，两者极为相似，但从评分上看X似乎不喜欢这2个内容，而Y比较喜欢，余弦相似度对数值的不敏感导致了结果的误差，需要修正这种不合理性）

 　　　 调整余弦相似度（Adjusted Cosine Similarity）

　　　　公式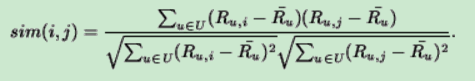：，其中Here  is the average of the u-th user's ratings.

　　　　2.2皮尔森相关系数（Pearson Correlation Coefficient）

　　　　定义：两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商

　　　　扩展

　　　　2.3Jaccard相似系数（Jaccard Coefficient）

　　　　公式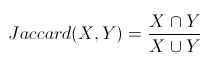：，这里X,Y不再是向量，而变成了集合

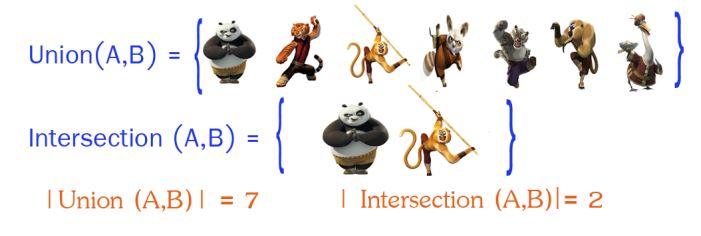
　　　　定义：Jaccard系数主要用于计算符号度量或布尔值度量的个体间的相似度，无法衡量差异具体值的大小，只能获得“是否相同”这个结果，所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。Jaccard系数等于样本集交集与样本集合集的比值。

　　　　计算：假设样本A和样本B是两个n维向量，而且所有维度的取值都是0或1。例如，A（0,1,1,0）和B（1,0,1,1）。我们将样本看成一个集合，1表示集合包含该元素，0表示集合不包含该元素。

　　　　p：样本A与B都是1的维度的个数

　　　　q：样本A是1而B是0的维度的个数

　　　　r：样本A是0而B是1的维度的个数

　　　　s：样本A与B都是0的维度的个数

　　　　那么样本A与B的杰卡德相似系数可以表示为：

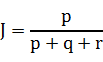
　　　　附：与Jaccard Coefficient相对应的是Jaccard 距离：d(X,Y) = 1 - Jaccard(X,Y);杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。(参考自余弦距离、欧氏距离和杰卡德相似性度量的对比分析)

　　　　2.4Tanimoto系数（广义Jaccard相似系数）

　　　　公式：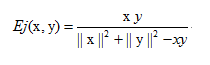

　　　　定义：广义Jaccard相似度，元素的取值可以是实数。又叫作谷本系数

　　　　关系：如果我们的x,y都是二值向量，那么Tanimoto系数就等同Jaccard距离。

　　　　2.5对数似然相似率

　　　　对于事件A和事件B，我们考虑两个事件发生的次数：

　　　　k11：事件A与事件B同时发生的次数
　　　　k12：B事件发生，A事件未发生
　　　　k21：A事件发生，B事件未发生
　　　　k22：事件A和事件B都未发生

　　　　
　　　　rowEntropy = entropy(k11, k12) + entropy(k21, k22)
　　　　columnEntropy = entropy(k11, k21) + entropy(k12, k22)
　　　　matrixEntropy = entropy(k11, k12, k21, k22)
　　　　2 * (matrixEntropy - rowEntropy - columnEntropy)

 　　　详情 扩展

　　　　2.6互信息/信息增益，相对熵/KL散度

　　　　互信息/信息增益：信息论中两个随机变量的相关性程度

　　　　公式：

　　　　相对熵/KL散度：又叫交叉熵，用来衡量两个取值为正数的函数（概率分布）的相似性

　　　　公式：

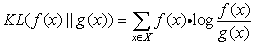
　　　　扩展：知乎问答

 　　　2.7信息检索--词频-逆文档频率（TF-IDF）

　　　　《数学之美》中看到的TF-IDF算法，在网页查询（Query）中相关性以词频（TF）与逆文档频率（IDF）来度量查询词（key）和网页(page)的相关性；

　　　　网页中出现key越多，该page与查询结果越相关，可以使用TF值来量化

　　　　每个词的权重越高，也即一个词的信息量越大；比如“原子能”就比“应用”的预测能力强，可以使用IDF值来量化，这里的IDF《数学之美》中说就是一个特定条件下关键词的概率分布的交叉熵。

　　      2.8词对相似度--点间相似度

3.距离算法与相似度算法的选择（对比）

　　3.1 欧式距离和余弦相似度

　　　　欧几里得距离度量会受指标不同单位刻度的影响，所以一般需要先进行标准化，同时距离越大，个体间差异越大

　　　　空间向量余弦夹角的相似度度量不会受指标刻度的影响，余弦值落于区间[-1,1]，值越大，差异越小

　　　　当两用户评分趋势一致时，但是评分值差距很大，余弦相似度倾向给出更优解。例如向量(3,3)和(5,5)，这两位用户的认知其实是一样的，但是欧式距离给出的解显然没有余弦值合理。

　　　　余弦相似度衡量的是维度间相对层面的差异，欧氏度量衡量数值上差异的绝对值；一种长度与方向的度量所造成的不同；余弦相似度只在［0，1］之间，而马氏距离在［0，无穷）之间（注：以上参考自知乎问题）

　　　　应用上如果要比较不同人的消费能力，可以使用欧式距离进行度量（价值度量）；如果想要比较不同用户是否喜欢周杰伦，可以使用余弦相似度（定性度量）

在数据分析和数据挖掘以及搜索引擎中，我们经常需要知道个体间差异的大小，进而评价个体的相似性和类别。常见的比如数据分析中比如相关分析，数据挖掘中的分类聚类（K-Means等）算法，搜索引擎进行物品推荐时。

相似度就是比较两个事物的相似性。一般通过计算事物的特征之间的距离，如果距离小，那么相似度大；如果距离大，那么相似度小。比如两种水果，将从颜色，大小，维生素含量等特征进行比较相似性。

欧氏距离是最常用的距离计算公式，衡量的是多维空间中各个点之间的绝对距离，当数据很稠密并且连续时，这是一种很好的计算方式。n维空间中的欧式距离的计算公式为：

因为计算是基于各维度特征的绝对数值，所以欧氏度量需要保证各维度指标在相同的刻度级别，比如对身高（cm）和体重（kg）两个单位不同的指标使用欧式距离可能使结果失效。 

在信息论中，两个等长字符串之间的海明距离是两个字符串对应位置的不同字符的个数。换句话说，它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。具体如下：

• "toned" and "roses" is 3.  “toned”和“roses”的海明距离是3。
• 1011101 and 1001001 is 2.  “1011101”和“1001001”的海明距离是2.
• 2173896 and 2233796 is 3.   “2173896”和“2233796”的海明距离是3.

• 

  三bit位海明距离立方体

  其中，100->011 海明距离为3， 010->111海明距离为2