本文主要是介绍LLM:Scaling Laws for Neural Language Models (上),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
论文:https://arxiv.org/pdf/2001.08361.pdf
发表:2020


摘要
1:损失与模型大小、数据集大小以及训练所用计算量成比例,其中一些趋势跨越了七个量级以上。
2:网络宽度或深度等其他架构细节在很大范围内影响较小。
3:模型/数据集大小和训练速度与模型大小的依赖关系由简单的方程描述。这些关系使我们能够确定在固定的计算预算下的最优资源分配。
4:更大的模型显著地更具样本效率,因此,在相对较小的数据量上训练非常大的模型并在收敛之前显著地停止。
发现
1:LLM模型的性能主要取决于scale,而不是model shape

模型性能强烈依赖于规模,这由三个因素组成:模型参数数量N(不包括嵌入)、数据集大小D和用于训练的计算C的数量。在合理的限度内,性能对其他架构超参数(例如深度与宽度的比较)的依赖非常弱。(第3节)
2:平滑的幂法则

当不受其他两个因素瓶颈的限制时,性能与三个规模因子N、D、C之间存在着强相关的幂关系,三个因素的趋势跨度超过六个量级(参见图1)。我们在上端没有观察到偏离这些趋势的迹象,尽管性能最终必须在达到零损失之前趋于平稳。(第3节)
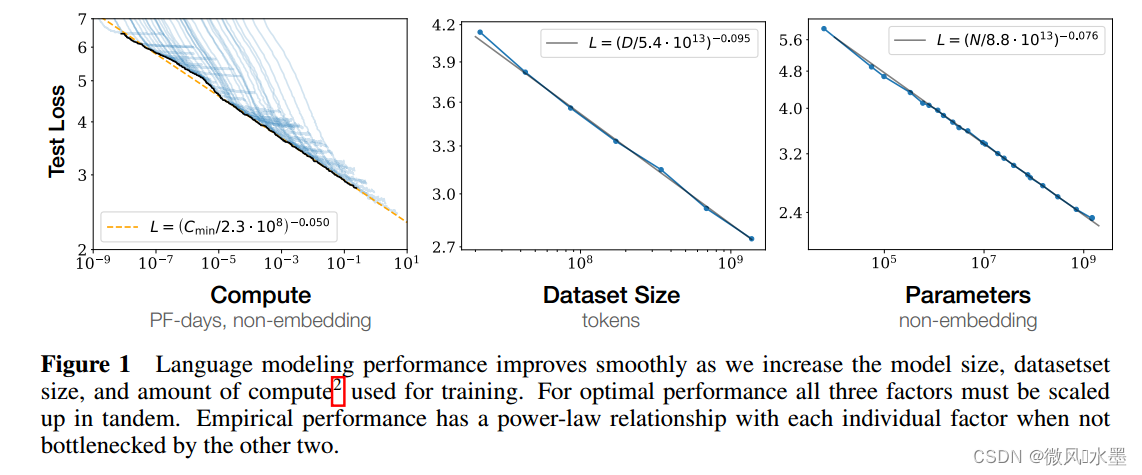
当我们增加模型大小N、数据规模D和训练时的计算量C,语言模型的性能会平稳提高。为了获得最佳性能,这三个因素需要同时缩放。实验表明:在其余两个参数不做限制条件下,测试Loss与另一个因素上都表现出幂关系。
3:过拟合的普遍性

同步增加模型大小N和数据规模D,模型性能就会显著地提高。但是,如果我们只固定N、D中的一个,而增加另一个规模,就会出现回报递减的情况。性能的惩罚可以预测地依赖于,这意味着我们每次将模型规模N增加8倍,只需将数据规模D增加5倍就可以避免受到惩罚。(第4节)
4:训练的普遍性

训练曲线遵循可预测的幂律,其参数大约独立于模型的大小。通过外推训练曲线的早期部分,我们可以大致预测如果我们训练更长时间会达到的损失。(第5节)
5:迁移能力随着测试性能的提高而提高

当我们在与模型训练数据分布不同的文本上评估模型时,结果与在训练验证集上的结果有强烈的相关性,但损失的偏移约为常数 - 换句话说,转移到不同的分布会产生一个常数的惩罚,但除此之外,性能大致与在训练集上的性能一致。 (第3.2.2节)
6:样本效率

大型模型比小型模式更具有样本效率,使用更少的优化步骤(图2)和更少的数据点(图4)就可以达到相同的性能水平。
紫色->绿色->黄色:表示模型的参数量N逐渐增大。
下图(左):收敛到相同水平(横线),大模型(黄色)需要的token数更少,即效率更高。
下图(右):收敛到相同水平(横线),小模型(黄色)耗时(PF-days)更少。
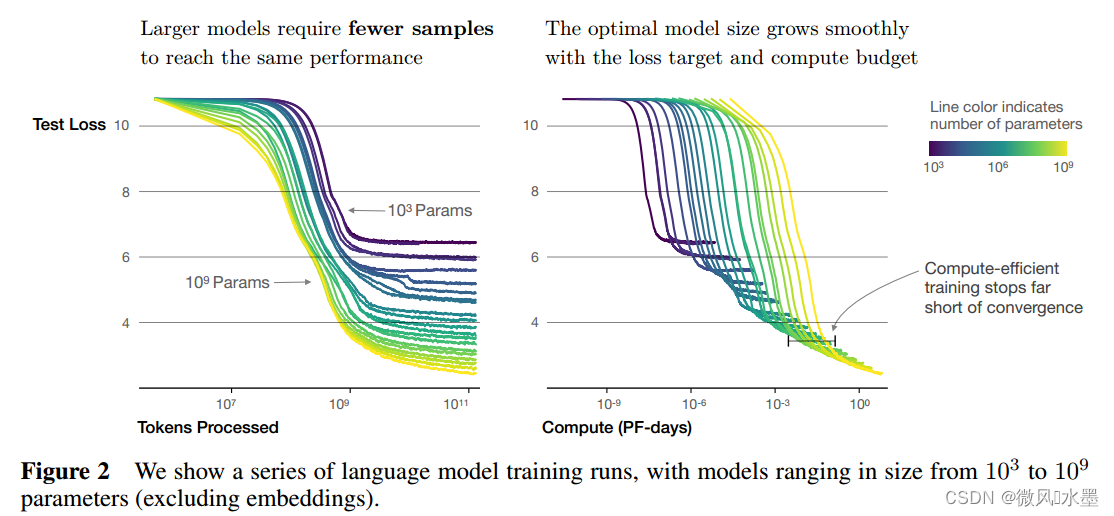
这里横轴单位为PF-days: 如果每秒钟可进行1015次运算,就是1 peta flops,那么一天的运算就是1015×24×3600=8.64×1019,这个算力消耗被称为1个petaflop/s-day。
7:收敛效率低下

固定计算量C,但不对模型规模N或可用数据规模D施加限制时,我们通过训练非常大的模型并在远未达到收敛的情况下停止(参见图3)来达到最佳性能。因此,最大化计算效率的训练将比基于训练小模型到收敛的预期更具有样本效率。数据要求随着的训练计算而增长非常缓慢。(第6节)
 对于计算效率最优的训练:大部分的计算能力应投放到模型尺寸增加上,小部分投入到数据增加上。在数据增加方面:主要是增加batch size,迭代steps基本可以忽略。从Fig3中可以看出:
对于计算效率最优的训练:大部分的计算能力应投放到模型尺寸增加上,小部分投入到数据增加上。在数据增加方面:主要是增加batch size,迭代steps基本可以忽略。从Fig3中可以看出:
model size : Batch size : serial steps = 1,000,000 : 100 : 10
8:最佳batch size
这些模型的理想批处理大小大致是损失的幂,并且可以通过测量梯度噪声尺度来确定。对于我们可以训练的最大模型,收敛时的理想批处理大 小约为 1-2 百万个token。(第 5.1 节)
2.2 训练流程
使用 Adam 优化器对模型进行固定 2.5×105 步的训练,批大小为 512 个序列,序列包含 1024 个词元。由于内存限制,我们使用 Adafactor对我们最大的模型(超过 1B 参数)进行训练。我们尝试了各种学习率和调度,如附录 D.6 中所述。我们发现收敛结果很大程度上与学习率调度无关。除非另有说明,我们数据中包含的所有训练运行都使用了一个学习率调度,该调度包括 3000 步线性预热,然后是余弦衰减到零。
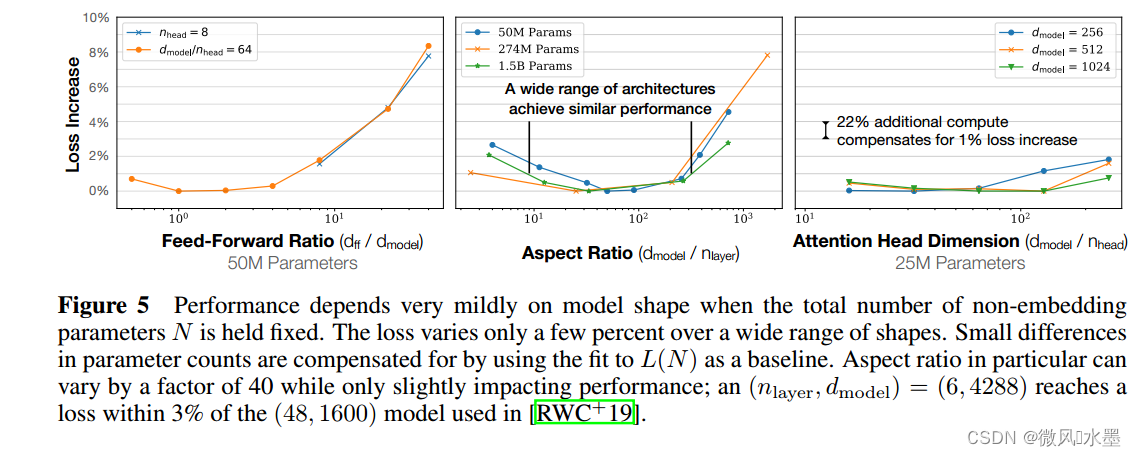
3.1 估计Transformer形状和超参数独立性
当我们保持总非嵌入参数计数 N 固定时,Transformer的性能对 nlayer 、 nheads 和 dff 等形状参数依赖性非常弱。
3.2 非嵌入参数计数 N 的性能

左图:当我们包括嵌入参数时,性能似乎除了参数数量外还强烈依赖于层数。
右图:当我们排除嵌入参数时,不同深度的模型的性能收敛到一个趋势。只有少于2层的模型或具有极端的深度宽度比的模型明显偏离趋势。
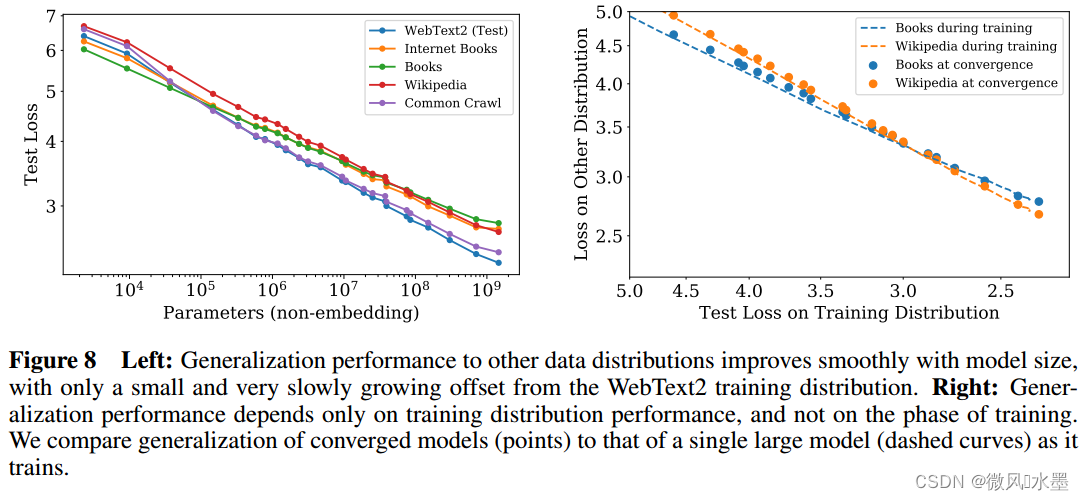
在WebText2数据集上训练的模型,在其他各种数据集上的测试损失也是 N 的幂律,且幂律几乎相同,如上图所示。
这篇关于LLM:Scaling Laws for Neural Language Models (上)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


![[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale](https://img-blog.csdnimg.cn/img_convert/172ed0ed26123345e1773ba0e0505cb3.png)