流体力学基础 | 雷诺时均RANS方程的推导从NS方程到RANS方程

本文主要是介绍流体力学基础 | 雷诺时均RANS方程的推导从NS方程到RANS方程，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1 前言

2 雷诺平均

2.1 基本思路

2.2 雷诺平均法则

3 紊流基本方程

4 雷诺应力

5 总结

1 前言

由上一篇内容，我们从原始形式的适用于所有流体的NS方程引入本构关系，获得了不可压缩牛顿流体的控制方程如下，该方程表征水沙瞬时运动的精确解。这里是链接。

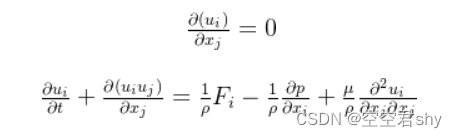
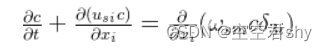
但是在实际的计算中，该方程组在大多数情况下由于计算成本的限制不能直接求解。且在工程计算中，我们对湍流运动的细节并不关注，怎么描述求解湍流平均运动是具有重要实际意义的。

2 雷诺平均

2.1 基本思路

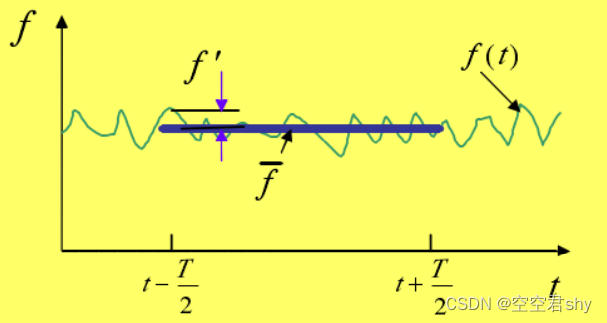
根据Reynolds的做法，瞬时物理量分为平均物理量mean quantity和脉动物理量fluctuating quantities，即

$\phi =\overline{\phi}+\phi'$

其中，上划线表示平均值，单撇表示脉动值。平均值为时间积分平均值，即

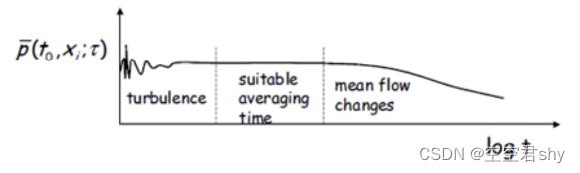
$\overline{\phi}=\frac{1}{T}\int_{t}^{t+T}\phi{}'d\tau$

T为考虑的时间段时均周期，T应当比湍流的脉动周期大得多，以便包含大量涨落，但应比宏观的流动特征时间小得多，以便充分描述时均值随时间t的变化。

脉动量满足如下关系

$\overline{(\phi{}')}=\frac{1}{T}\int_{t}^{t+T}\phi{}'d\tau=0$

2.2 雷诺平均法则

根据以上雷诺平均的定义，我们可以得到如下雷诺平均法则】

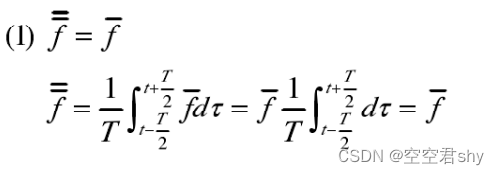
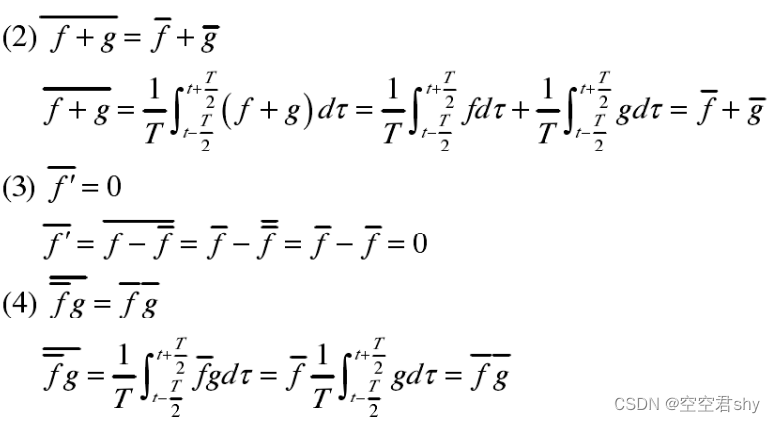
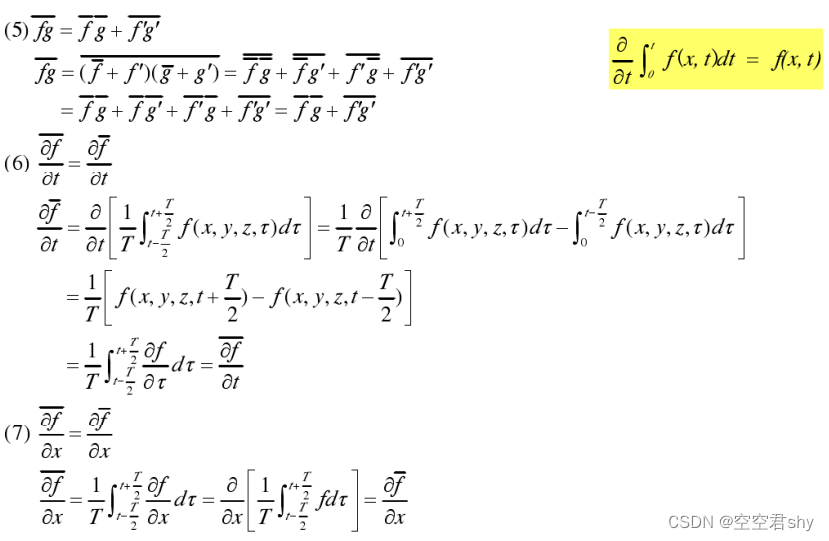
3 紊流基本方程

应用以上雷诺平均的思想，对连续性方程，运动方程和泥沙方程进行时均化得到

$\frac{\partial \overline{\rho } }{\partial t}+\frac{\partial \overline{\rho} \overline{u_i}}{\partial x_i}=0$

$\frac{\partial \overline{\rho} \overline{u_i}}{\partial t}+\frac{\partial \overline{\rho u_i u_j}}{\partial x_j}=\overline{F_i}-\frac{\partial \overline{p}}{\partial x_i}+\mu \frac{\partial^2{\overline{u_i}}}{\partial{x_i} \partial{x_j}}-\frac{\partial{\overline{\rho u_i{}' u_j{}'}}}{\partial x_j}$

$\frac{\partial \overline{c}}{\partial t}+\frac{\partial \overline{u_i c}}{\partial x_i}=\frac{\partial }{\partial x_i}(\omega _s\overline{c}\delta _{3i})-\frac{\partial \overline{u_i{}'c{}'}}{\partial{x_i}}$

其中 $\overline{u_i{}'u_j{}'}$ 与xi和xj方向的脉动速度有关。从物理含义上来说， $-\rho \overline{u_i{}'u_j{}'}$ 表征湍流引起的动量输运，称为雷诺应力或湍流应力。 $-\overline{u_i{}'c{}'}$ 为湍流泥沙通量，表征湍流引起的泥沙输移。

对于含沙量较小的情况，即ρ不变时的方程如下

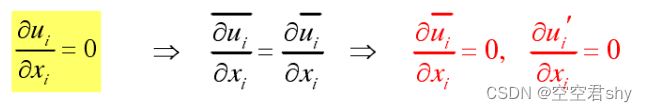
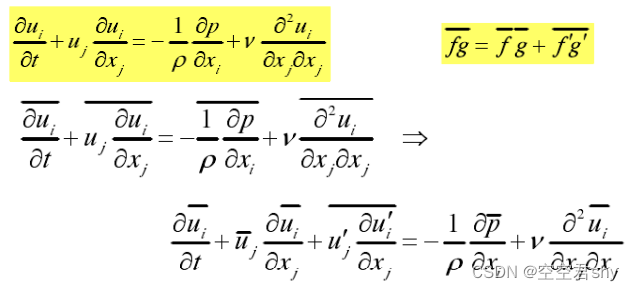
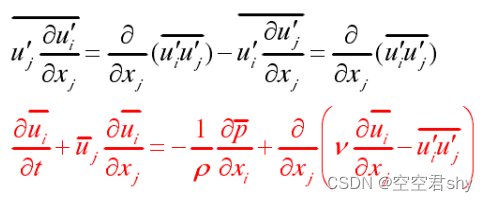
以上三个方程即为雷诺平均的水沙运动控制方程，其中前两个描述水流运动的方程称为雷诺时均方程（RANS方程）。然而，由于湍流应力的存在，该方程组并不封闭，需要引入格外的湍流模式对方程组进行封闭。

4 雷诺应力

根据雷诺平均的N-S方程，我们定义紊流平均场中的总应力张量δij为：

$\sigma _{ij}=-p \delta_{ij}+\tau_{ij}+\tau _{ij}{}'$

其中p即为压应力；τij为平均切应力，在水动力学方程中主要为河床阻力，通过曼宁公式计算；τij'为雷诺应力，通过湍流封闭模式计算。

根据牛顿内摩擦定律的扩展形式，我们认为

$\tau _{ij}=\mu(\frac{\partial {\overline{u_i}}}{\partial{x_j}}+\frac{\partial {\overline{u_j}}}{\partial{x_i}})$

表征分子粘性切应力，由于其和雷诺应力相比属于小量，因此在一般的水动力学模型计算中可以忽略。雷诺应力的矩阵形式为

$\tau_{ij}{}'=-\rho \overline{u_i{}'u_j{}'}=\begin{bmatrix} -\rho\overline{u{}'^2} \ -\rho\overline{u{}'v{'}} \ -\rho\overline{u{'}w{'}} & & \\ -\rho\overline{u{}'v{'}} \ -\rho\overline{v{}'^2}\ -\rho\overline{v{'}w{'}} & & \\ -\rho\overline{u{'}w{'}} \ -\rho\overline{v{'}w{'}} \ -\rho\overline{w{'}^2} \end{bmatrix}$