斯坦福 Stats60：21 世纪的统计学：第五章到第九章

本文主要是介绍斯坦福 Stats60：21 世纪的统计学：第五章到第九章，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第五章：将模型拟合到数据

原文：statsthinking21.github.io/statsthinking21-core-site/fitting-models.html

译者：飞龙

协议：CC BY-NC-SA 4.0

统计学中的一个基本活动是创建能够用少量数字总结数据的模型，从而提供数据的简洁描述。在本章中，我们将讨论统计模型的概念以及如何用它来描述数据。

5.1 什么是模型？

在物理世界中，“模型”通常是对现实世界中的事物的简化，但仍然传达了被建模事物的本质。建筑物的模型传达了建筑物的结构，同时足够小和轻，可以用一只手拿起；生物学中细胞的模型比实际的细胞大得多，但同样传达了细胞的主要部分及其关系。

在统计学中，模型的目的是提供一个类似的简洁描述，但是针对的是数据而不是物理结构。与物理模型一样，统计模型通常比所描述的数据简单得多；它的目的是尽可能简单地捕捉数据的结构。在这两种情况下，我们意识到模型是一个方便的虚构，必然忽略了被建模的实际细节。正如统计学家 George Box 所说：“所有模型都是错误的，但有些是有用的。”将统计模型视为观察数据生成方式的理论也是有用的；我们的目标是找到最有效和准确地总结数据生成方式的模型。但正如我们将在下面看到的，效率和准确性的要求通常是截然相反的。

统计模型的基本结构是：

$$数据=模型+误差$$

这表达了这样一个观点：数据可以分为两部分：一部分由统计模型描述，它表达了我们根据我们的知识期望数据采取的值，另一部分我们称之为误差，它反映了模型预测和观察数据之间的差异。

实质上，我们希望使用我们的模型来预测任何给定观察的数据值。我们会这样写方程：

$$\widehat{dat{a}_i}=mode{l}_i$$

数据上的“帽子”表示这是我们的预测，而不是数据的实际值。这意味着观察$i$的数据的预测值等于该观察的模型值。一旦我们从模型得到预测，我们就可以计算误差：

$$erro{r}_i=dat{a}_i-\widehat{dat{a}_i}$$

也就是说，任何观察的误差是数据的观察值与模型预测值之间的差异。

5.2 统计建模：一个例子

让我们看一个建立数据模型的例子，使用 NHANES 的数据。特别是，我们将尝试建立 NHANES 样本中儿童身高的模型。首先让我们加载数据并绘制它们（参见图 5.1）。

图 5.1：NHANES 儿童身高的直方图。

请记住，我们希望尽可能简单地描述数据，同时仍然捕捉到它们的重要特征。我们可以想象的最简单的模型将只涉及一个单一的数字；也就是说，该模型将预测每个观察值相同的值，而不管我们可能了解这些观察值的其他信息。我们通常用参数来描述模型，这些参数是我们可以改变以修改模型预测的值。在整本书中，我们将使用希腊字母 beta（$\beta$）来指代这些参数；当模型有多个参数时，我们将使用带下标的数字来表示不同的 beta（例如${\beta }_1$）。习惯上，我们用字母$y$来表示数据的值，并使用带下标的版本$y_i$来表示个别观察值。

我们通常不知道参数的真实值，因此我们必须从数据中估计它们。因此，我们通常会在$\beta$符号上放一个“帽子”，表示我们使用的是参数值的估计值，而不是它的真实值（通常我们不知道）。因此，我们使用单个参数对身高的简单模型将是：

$$y_i=\beta +ϵ$$

方程的右侧没有出现下标$i$，这意味着模型的预测不取决于我们正在观察的是哪个观察值——对所有观察值都是相同的。那么问题就变成了：我们如何估计模型参数的最佳值？在这种情况下，什么单个值是$\beta$的最佳估计？更重要的是，我们如何定义最佳？

我们可能想象的一个非常简单的估计量是模式，它只是数据集中最常见的值。这将整个 1691 个孩子的数据重新描述为一个单一的数字。如果我们想要预测任何新孩子的身高，那么我们的预测值将是相同的数字：

$$\widehat{y_i}=166.5$$

然后，每个个体的误差将是预测值（$\widehat{y_i}$）与他们实际身高（$y_i$）之间的差异：

$$erro{r}_i=y_i-\widehat{y_i}$$

这个模型有多好呢？通常我们根据误差的大小来定义模型的好坏，误差代表数据偏离模型预测的程度；其他条件相同，产生较小误差的模型更好。（尽管后面我们会看到，其他条件通常不相同…）在这种情况下，我们发现当我们使用模式作为$\beta$的估计量时，平均个体的误差相当大，为-28.8 厘米，这在表面上看起来并不好。

我们如何找到一个更好的模型参数估计量？我们可以尝试找到一个使平均误差为零的估计量。一个很好的选择是算术平均值（即平均值，通常用变量上方的横线表示，如$\bar{X}$），计算为所有值的总和除以值的数量。在数学上，我们表示为：

$$\bar{X}=\frac{{\sum }_{i=1}^n{x}_i}{n}$$

事实证明，如果我们使用算术平均值作为我们的估计量，那么平均误差确实将为零（如果您感兴趣，可以在本章末尾看到简单的证明）。尽管从平均值的误差是零，但我们可以从图 5.2 的直方图中看到，每个个体仍然有一定程度的误差；有些是正的，有些是负的，它们相互抵消，使平均误差为零。

图 5.2：从平均值的误差分布。

负误差和正误差相互抵消的事实意味着两个不同的模型在绝对值上可能具有非常不同的误差量，但仍然具有相同的平均误差。这正是为什么平均误差不是我们估计器的良好标准的原因；我们希望一个试图最小化总体误差的标准，而不考虑其方向。因此，我们通常根据某种计算正负误差的度量来总结错误。我们可以使用每个误差值的绝对值，但更常见的是使用平方误差，原因我们将在本书的后面看到。

有几种常见的方法来总结平方误差，您将在本书的各个部分遇到，因此了解它们之间的关系很重要。首先，我们可以简单地将它们相加；这被称为平方误差的总和。我们通常不使用它的原因是它的大小取决于数据点的数量，因此除非我们观察相同数量的观察结果，否则很难解释。其次，我们可以取平方误差值的平均值，这被称为均方误差（MSE）。然而，由于我们在平均值之前对值进行了平方，它们与原始数据不在同一尺度上；它们是在$厘{米}^2$。因此，通常也会取均方误差的平方根，我们称之为均方根误差（RMSE），以便误差以与原始值相同的单位（在本例中为厘米）来衡量。

均值有相当大的误差-任何个体数据点平均将偏离均值约 27 厘米-但仍然比众数要好得多，众数的均方根误差约为 39 厘米。

5.2.1 改进我们的模型

我们能想象一个更好的模型吗？请记住，这些数据来自 NHANES 样本中所有 2 至 17 岁的儿童，他们的年龄变化很大。鉴于这一广泛的年龄范围，我们可能期望我们的身高模型也应包括年龄。让我们绘制身高与年龄的数据，看看这种关系是否真的存在。

图 5.3：NHANES 中儿童的身高，没有模型绘制（A），只包括年龄的线性模型（B）或年龄和常数的线性模型（C），以及适合男女年龄的线性模型（D）。

图 5.3 的面板 A 中的黑点显示了数据集中的个体，身高和年龄之间似乎存在着很强的关系，这是我们所期望的。因此，我们可能会建立一个将身高与年龄相关联的模型：

$$\widehat{y_i}=\hat{\beta }\ast ag{e}_i$$

其中$\hat{\beta }$是我们估计的参数，我们将其乘以年龄以生成模型预测。

您可能还记得代数中定义线的方式：

$$y=斜率\ast x+截距$$

如果年龄是 $X$ 变量，那么这意味着我们从年龄对身高的预测将是一条斜率为 $\beta$ 截距为零的直线——为了看到这一点，让我们在数据上用蓝色绘制最佳拟合线（图 5.3 的 B 面板）。显然，这个模型有明显的问题，因为这条线似乎并不很好地跟随数据。事实上，这个模型的均方根误差（39.16）实际上比只包括均值的模型还要高！问题在于我们的模型只包括年龄，这意味着模型对于年龄为零时的身高预测值必须为零。即使数据中没有任何年龄为零的儿童，数学上要求这条线在 x 为零时有一个 y 值为零，这就解释了为什么这条线被拉到了年轻数据点的下方。我们可以通过在模型中包括一个截距来解决这个问题，这基本上代表了当年龄等于零时的估计身高；即使在这个数据集中年龄为零是不合理的，这是一个数学技巧，可以让模型考虑到数据的整体幅度。模型是：

$$\widehat{y_i}=\widehat{{\beta }_0}+\widehat{{\beta }_1}\ast ag{e}_i$$

其中 $\widehat{{\beta }_0}$ 是我们对 截距 的估计，它是添加到每个个体预测值的常数值；我们称之为截距，因为它映射到直线方程中的截距。我们将在后面学习如何为特定数据集估计这些参数值；现在，我们将使用我们的统计软件来估计给出这些特定数据最小误差的参数值。图 5.3 的 C 面板显示了这个模型应用于 NHANES 数据，我们可以看到，这条线比没有常数的那条线更好地匹配了数据。

我们使用这个模型的误差要小得多——平均只有 8.36 厘米。你能想到其他可能与身高有关的变量吗？性别呢？在图 5.3 的 D 面板中，我们分别为男性和女性绘制了拟合线的数据。从图中看，似乎男性和女性之间存在差异，但这种差异相对较小，并且只在青春期后才显现。在图 5.4 中，我们绘制了不同模型的均方根误差值，包括一个额外参数来模拟性别的影响。从中我们可以看到，模型从模式到均值变得更好了一点，从均值到均值+年龄变得更好了很多，而包括性别后只稍微变得更好了一点。

图 5.4：对上面测试的每个模型绘制的均方误差。

5.3 什么使一个模型“好”？

我们通常希望从我们的统计模型中得到两种不同的东西。首先，我们希望它能很好地描述我们的数据；也就是说，我们希望在对数据建模时，它的误差尽可能低。其次，我们希望它能很好地推广到新的数据集；也就是说，当我们将其应用于新的数据集以进行预测时，我们希望它的误差尽可能低。事实证明，这两个特性经常会发生冲突。

为了理解这一点，让我们思考误差的来源。首先，如果我们的模型是错误的，误差就会产生；例如，如果我们错误地说身高随着年龄下降而不是上升，那么我们的误差将比正确模型的误差更大。同样，如果我们的模型中缺少一个重要因素，那也会增加我们的误差（就像我们在身高模型中没有考虑年龄时那样）。然而，即使模型是正确的，误差也可能发生，这是由于数据的随机变化造成的，我们通常称之为“测量误差”或“噪音”。有时，这确实是由于我们测量的错误 - 例如，当测量依赖于人类时，比如使用秒表来测量足球比赛中的经过时间。在其他情况下，我们的测量设备非常精确（比如用于测量体重的数字秤），但被测量的物体受到许多不同因素的影响，导致它变化。如果我们知道所有这些因素，那么我们就可以建立一个更准确的模型，但实际上这很少可能。

让我们用一个例子来说明这一点。我们将使用计算机模拟生成一些数据来进行示例，而不是使用真实数据（关于这一点我们将在几章后详细讨论）。假设我们想要了解一个人的血液酒精含量（BAC）与他们在模拟驾驶测试中的反应时间之间的关系。我们可以生成一些模拟数据并绘制关系（参见图 5.5 的 A 面）。

图 5.5：在驾驶测试中血液酒精含量和反应时间之间的模拟关系，最佳拟合线性模型由线表示。A：与低测量误差的线性关系。B：与较高测量误差的线性关系。C：与低测量误差和（不正确的）线性模型的非线性关系

在这个例子中，反应时间随着血液酒精含量的增加而系统性增加 - 线条显示了最佳拟合模型，我们可以看到误差非常小，这在所有点都非常接近线条的事实中是显而易见的。

我们还可以想象出现相同线性关系的数据，但误差更大，就像图 5.5 的 B 面所示。在这里，我们可以看到反应时间随着血液酒精含量的增加仍然存在系统性增加，但在个体之间的变异性更大。

这些都是两个变量之间关系呈现线性的例子，误差反映了我们测量中的噪音。另一方面，还有其他情况下，变量之间的关系不是线性的，误差会增加，因为模型没有正确规定。比如，我们对咖啡因摄入量和测试表现之间的关系感兴趣。咖啡因等兴奋剂与测试表现之间的关系通常是非线性的 - 也就是说，它不是一条直线。这是因为测试表现随着较小剂量的咖啡因而提高（人变得更警觉），但随着较大剂量的咖啡因而开始下降（人变得紧张和焦虑）。我们可以模拟这种形式的数据，然后对数据进行线性模型拟合（参见图 5.5 的 C 面板）。蓝线显示了最适合这些数据的直线；显然，误差很大。尽管测试表现和咖啡因摄入之间存在非常合法的关系，但它遵循的是曲线而不是直线。假设线性关系的模型由于这些数据而产生了高误差，因为它对这些数据来说是错误的模型。

5.4 模型是否可能太好？

误差听起来像是一件坏事，通常我们会更喜欢具有较低误差的模型，而不是具有较高误差的模型。然而，我们上面提到，模型在准确拟合当前数据集和泛化到新数据集之间存在紧张关系，事实证明，具有最低误差的模型通常在泛化到新数据集时要比较差！

为了看到这一点，让我们再次生成一些数据，以便我们知道变量之间的真实关系。我们将创建两个模拟数据集，它们以完全相同的方式生成 - 只是它们分别添加了不同的随机噪声。也就是说，它们的方程式都是$y=\beta \ast X+ϵ$；唯一的区别是在每种情况下，$ϵ$使用了不同的随机噪声。

图 5.6：过度拟合的一个例子。两个数据集都是使用相同的模型生成的，每个集合都添加了不同的随机噪声。左面板显示了用于拟合模型的数据，蓝色表示简单线性拟合，红色表示复杂（8 阶多项式）拟合。图中显示了每个模型的均方根误差（RMSE）值；在这种情况下，复杂模型的 RMSE 低于简单模型。右面板显示了第二个数据集，上面覆盖了相同的模型，并使用从第一个数据集获得的模型计算了 RMSE 值。在这里，我们看到简单模型实际上比过度拟合到第一个数据集的更复杂模型更好地适应了新数据集。

图 5.6 的左面板显示，更复杂的模型（红色）比更简单的模型（蓝色）更好地拟合了数据。然而，当相同的模型应用于以相同方式生成的新数据集时，我们看到相反的情况-在这里，我们看到更简单的模型比更复杂的模型更好地拟合了新数据。直观地，我们可以看到更复杂的模型受到第一个数据集中特定数据点的影响很大;由于这些数据点的确切位置是由随机噪声驱动的，这导致更复杂的模型在新数据集上拟合不佳。这是我们所说的过度拟合现象。现在重要的是要记住，我们的模型拟合需要很好，但不要太好。正如阿尔伯特·爱因斯坦（1933 年）所说：“可以毫不夸张地说，所有理论的最高目标是使不可简化的基本元素尽可能简单，尽可能少，而不必放弃对单个经验数据的充分表征。”这经常被改编为：“一切都应该尽可能简单，但不要太简单。”

5.5 使用均值总结数据

我们已经遇到了均值（或平均值），实际上大多数人都知道平均值，即使他们从未上过统计课。它通常用来描述我们所说的数据集的“中心趋势”-也就是说，数据以什么值为中心？大多数人并不认为计算均值是将模型拟合到数据。然而，当我们计算均值时，这正是我们正在做的。

我们已经看到了计算样本数据均值的公式：

$$\bar{X}=\frac{{\sum }_{i=1}^n{x}_i}{n}$$

请注意，我说过这个公式是特别针对样本数据的，这是从更大的人口中选择的一组数据点。使用样本，我们希望描述更大的人口-我们感兴趣的所有个体的完整集合。例如，如果我们是政治民意调查员，我们感兴趣的人口可能是所有注册选民，而我们的样本可能只包括从该人口中抽样的几千人。在第 7 章中，我们将更详细地讨论抽样，但现在重要的是统计学家通常喜欢使用不同的符号来区分描述样本值的统计量和描述人口真实值的参数;在这种情况下，人口均值的公式（表示为$\mu$）是：

$$\mu =\frac{{\sum }_{i=1}^N{x}_i}{N}$$

其中 N 是整个人口的大小。

我们已经看到均值是一个保证给我们平均误差为零的估计量，但我们也学到了平均误差不是最好的标准；相反，我们希望一个给出最低平方误差和（SSE）的估计量，而均值也能做到。我们可以用微积分来证明这一点，但我们将在图 5.7 中用图形来演示它。

图 5.7：演示均值作为最小化平方误差和的统计量。使用 NHANES 儿童身高数据，我们计算均值（用蓝色条表示）。然后，我们测试一系列可能的参数估计值，对于每个值，我们计算每个数据点与该值之间的平方误差和，用黑色曲线表示。我们看到均值落在平方误差图的最小值处。

最小化 SSE 是一个很好的特性，这就是为什么平均值是最常用的总结数据的统计量。然而，平均值也有一个不好的一面。比如说有五个人在酒吧，我们检查每个人的收入（表 5.1）：

表 5.1：我们五个酒吧顾客的收入

收入	人
48000	乔
64000	卡伦
58000	马克
72000	安德烈
66000	帕特

平均值（61600.00）似乎是对这五个人的收入的一个很好的总结。现在让我们看看如果碧昂丝·诺尔斯走进酒吧会发生什么（表 5.2）。

表 5.2：我们五个酒吧顾客加上碧昂丝·诺尔斯的收入。

收入	人
48000	乔
64000	卡伦
58000	马克
72000	安德烈
66000	帕特
54000000	碧昂丝

现在平均值接近 1000 万美元，这实际上并不代表酒吧里的任何人 - 特别是，它受到碧昂丝这个异常值的极大影响。一般来说，平均值对极端值非常敏感，这就是为什么在使用平均值总结数据时，确保没有极端值总是很重要的原因。

5.5.1 使用中位数稳健地总结数据

如果我们想以一种对异常值不太敏感的方式总结数据，我们可以使用另一个叫做中位数的统计量。如果我们按照大小顺序对所有值进行排序，那么中位数就是中间的值。如果值的数量是偶数，那么会有两个值并列在中间位置，这种情况下我们取这两个数的平均值（即两个数的中间点）。

让我们看一个例子。假设我们想总结以下值：

8  6  3 14 12  7  6  4  9

如果我们对这些值进行排序：

3  4  6  6  7  8  9 12 14

然后中位数是中间值 - 在这种情况下，是 9 个值中的第 5 个。

而平均值最小化了平方误差的和，中位数最小化了一个略有不同的数量：误差的绝对值的和。这解释了为什么中位数对异常值不太敏感 - 平方会加剧大误差的影响，而绝对值不会。我们可以从收入的例子中看到这一点：中位收入（$65,000）更能代表整个群体，而不太敏感于一个大的异常值，而平均值（$9,051,333）。

鉴于此，我们为什么还要使用平均值呢？正如我们将在后面的章节中看到的，平均值是“最好的”估计量，因为它在样本之间的变化要比其他估计量小。这取决于我们是否认为这值得对潜在异常值的敏感性 - 统计学就是关于权衡的。

5.6 众数

有时我们希望描述一个非数值数据集的中心趋势。例如，假设我们想知道哪种型号的 iPhone 最常用。为了测试这一点，我们可以问一大群 iPhone 用户每个人拥有哪种型号。如果我们对这些值取平均值，我们可能会发现平均 iPhone 型号是 9.51，这显然是荒谬的，因为 iPhone 型号并不是量化的测量。在这种情况下，中心趋势的更合适的度量是众数，即数据集中最常见的值，正如我们上面讨论的那样。

5.7 变异性：平均值对数据拟合得有多好？

一旦我们描述了数据的中心趋势，我们通常也想描述数据的变异程度 - 这有时也被称为“离散度”，反映了它描述数据有多广泛分布的事实。

我们已经在上面遇到了平方误差的总和，这是最常用的变异性度量的基础：方差和标准差。人口的方差（表示为${\sigma }^2$）简单地是平方误差的总和除以观察次数 - 也就是说，它与之前遇到的均方误差完全相同：

$${\sigma }^2=\frac{SSE}{N}=\frac{{\sum }_{i=1}^n(x_i-\mu {)}^2}{N}$$

其中$\mu$是总体均值。总体标准差简单地是这个的平方根 - 也就是我们之前看到的均方根误差。标准差很有用，因为误差与原始数据的单位相同（撤销了我们对误差的平方）。

通常我们无法访问整个总体，所以我们必须使用样本来计算方差，我们称之为${\hat{\sigma }}^2$，其中“帽子”表示这是基于样本的估计。${\hat{\sigma }}^2$的方程与${\sigma }^2$的方程类似：

$${\hat{\sigma }}^2=\frac{{\sum }_{i=1}^n(x_i-\bar{X}{)}^2}{n-1}$$

两个方程之间唯一的区别是我们除以 n-1 而不是 N。这涉及到一个基本的统计概念：自由度。记住，为了计算样本方差，我们首先必须估计样本均值$\bar{X}$。在估计了这个值之后，数据中的一个值就不再自由变化。例如，假设我们有一个变量$x$的以下数据点：[3, 5, 7, 9, 11]，其均值为 7。因为我们知道这个数据集的均值是 7，我们可以计算如果缺少任何特定值的值。例如，假设我们要隐藏第一个值（3）。这样做之后，我们仍然知道它的值必须是 3，因为 7 的均值意味着所有值的总和是$7\ast n=35$，$35-(5+7+9+11)=3$。

所以当我们说我们“失去”了一个自由度时，这意味着在拟合模型后有一个值不再自由变化。在样本方差的背景下，如果我们不考虑失去的自由度，那么我们对样本方差的估计将是有偏的，导致我们低估了对均值估计的不确定性。

5.8 使用模拟来理解统计学

我坚信使用计算机模拟来理解统计概念，在后面的章节中我们将更深入地探讨它们的使用。在这里，我们将通过询问是否可以确认在计算样本方差时需要从样本大小中减去 1 来介绍这个想法。

让我们把 NHANES 数据中的所有儿童样本作为我们的“总体”，并看看使用分母中的$n$或$n-1$来计算样本方差会如何估计这个总体的方差，在从数据中模拟的大量随机样本中。我们将在后面的章节中详细介绍如何做到这一点。

表 5.3：使用 n 与 n-1 的方差估计；使用 n-1 的估计更接近于总体值

估计	值
总体方差	725
使用 n 的方差估计	710
使用 n-1 的方差估计	725

5.3 中的结果告诉我们，上面概述的理论是正确的：使用$n-1$作为分母的方差估计非常接近于在完整数据（即总体）上计算的方差，而使用$n$作为分母的方差估计是有偏的（较小），与真实值相比。

5.9 Z 分数

在以中心趋势和变异性来表征分布之后，通常有必要以个体得分在整体分布中的位置来表达。假设我们有兴趣描述不同州之间犯罪的相对水平，以确定加利福尼亚是否是一个特别危险的地方。我们可以使用来自FBI 统一犯罪报告网站的 2014 年数据来提出这个问题。图 5.8 的左侧面板显示了每个州暴力犯罪数量的直方图，突出显示了加利福尼亚的值。从这些数据来看，加利福尼亚似乎非常危险，当年有 153709 起犯罪。我们可以通过生成一张地图来可视化这些数据，显示一个变量在各州之间的分布，这在图 5.8 的右侧面板中呈现。

图 5.8：左侧：暴力犯罪数量的直方图。 CA 的值以蓝色绘制。右侧：相同数据的地图，以各州的犯罪数量（以千为单位）用颜色表示。

然而，您可能已经意识到，加利福尼亚也是美国人口最多的州，因此它拥有更多的犯罪是合理的。如果我们将每个州的犯罪数量与人口之一绘制成图（参见图 5.9 的左侧面板），我们会发现两个变量之间存在直接关系。

图 5.9：左侧：按州划分的暴力犯罪数量与人口的图。右侧：以每 10 万人口的犯罪率表示的暴力犯罪率的直方图。

我们应该使用每人口的暴力犯罪率，而不是使用原始犯罪数字，这可以通过将每个州的犯罪数量除以每个州的人口来获得。FBI 的数据集已经包括了这个值（以每 10 万人口的比率表示）。从图 5.9 的右侧面板可以看出，加利福尼亚并不那么危险 - 其每 10 万人口的犯罪率为 396.10，略高于各州的平均值 346.81，但远低于许多其他州。但是，如果我们想更清楚地了解它与其他分布的距离有多远呢？

Z 得分允许我们以一种更能洞察每个数据点与整体分布关系的方式来表达数据。计算给定个体数据点的 Z 得分的公式，假设我们知道总体均值$\mu$和标准偏差$\sigma$的值为：

$$Z(x)=\frac{x-\mu }{\sigma }$$

直观地，您可以将 Z 得分视为告诉您任何数据点距离平均值有多远，以标准偏差为单位。我们可以计算犯罪率数据的 Z 得分，如图 5.10 所示，该图将 Z 得分绘制为原始得分。

图 5.10：原始犯罪率数据与 Z 得分数据的散点图。

散点图告诉我们，Z 分数的过程并不改变数据点的相对分布（在原始数据和 Z 分数数据相互绘制时，它们落在一条直线上），它只是将它们移动到具有零均值和标准偏差为一的位置。图 5.11 显示了使用地理视图的 Z 分数犯罪数据。

图 5.11：犯罪数据呈现为 Z 分数的美国地图。

这为我们提供了对数据稍微更易解释的视角。例如，我们可以看到内华达州、田纳西州和新墨西哥州的犯罪率大约是平均值的两个标准偏差。

5.9.1 解释 Z 分数

“Z 分数”中的“Z”来自于标准正态分布（即均值为零，标准偏差为 1 的正态分布）通常被称为“Z”分布。我们可以使用标准正态分布来帮助我们理解特定 Z 分数告诉我们关于数据点在分布的其余部分中所处位置的信息。

图 5.12：标准正态分布的密度（上）和累积分布（下），在一个标准偏差以上/以下的均值处有截断。

图 5.12 的上部显示我们预计大约 16%的值落在$Z\ge 1$，同样的比例落在$Z\le -1$。

图 5.13：标准正态分布的密度（上）和累积分布（下），在两个标准偏差以上/以下的均值处有截断。

图 5.13 显示了两个标准偏差的相同图。在这里，我们看到只有大约 2.3%的值落在$Z\le -2$，同样的在$Z\ge 2$。因此，如果我们知道特定数据点的 Z 分数，我们可以估计找到至少与该值一样极端的值的可能性或不可能性，这让我们更好地将值放入上下文中。在犯罪率的情况下，我们看到加利福尼亚的暴力犯罪率人均 Z 分数为 0.38，显示它与其他州的平均值相当接近，大约有 35%的州有更高的犯罪率，65%的州有更低的犯罪率。

5.9.2 标准化分数

假设我们不是用 Z 分数，而是想生成平均值为 100，标准偏差为 10 的标准化犯罪分数。这类似于对智力测试分数进行标准化以生成智商指数（IQ）。我们可以通过简单地将 Z 分数乘以 10 然后加上 100 来实现这一点。

图 5.14：犯罪数据以平均值为 100，标准偏差为 10 呈现为标准化分数。

5.9.2.1 使用 Z 分数比较分布

Z 得分的一个有用应用是比较不同变量的分布。假设我们想要比较各州的暴力犯罪和财产犯罪的分布。在图 5.15 的左面板中，我们将它们相互绘制，CA 用蓝色绘制。正如你所看到的，财产犯罪的原始率远高于暴力犯罪的原始率，所以我们不能直接比较这些数字。然而，我们可以将这些数据的 Z 得分相互绘制（图 5.15 的右面板）- 在这里我们再次看到数据的分布没有改变。将每个变量的数据转换为 Z 得分使它们可以相互比较，并让我们看到加利福尼亚实际上在暴力犯罪和财产犯罪方面都处于分布的中间位置。

图 5.15：暴力犯罪率与财产犯罪率的图表（左）和 Z 得分率（右）。

让我们在图中再添加一个因素：人口。在图 5.16 的左面板中，我们使用绘图符号的大小来显示这一点，这通常是向图中添加信息的有用方式。

图 5.16：左：暴力犯罪率与财产犯罪率的图表，通过绘图符号的大小呈现人口规模；加利福尼亚以蓝色呈现。右：暴力犯罪与财产犯罪的差异分数，绘制在人口上。

因为 Z 得分是直接可比较的，我们还可以计算一个差异分数，它表达了各州暴力与非暴力（财产）犯罪的相对率。然后我们可以将这些分数绘制在人口上（参见图 5.16 的右面板）。这显示了我们如何使用 Z 得分将不同的变量放在一个共同的尺度上。

值得注意的是，最小的州似乎在两个方向上都有最大的差异。虽然可能会诱人地查看每个州并尝试确定为什么它具有高或低的差异分数，但这可能反映了从较小样本中获得的估计值必然会更加变化，正如我们将在第 7 章中讨论的那样。

5.10 学习目标

• 描述统计模型的基本方程（数据=模型+误差）

• 描述不同的集中趋势和离散度测量，它们是如何计算的，以及在什么情况下适用。

• 计算 Z 得分并描述它们为什么有用。

5.11 附录

5.11.1 证明均值误差的总和为零

$$错误=\sum _{i=1}^n(x_i-\bar{X})=0$$

$$\sum _{i=1}^n{x}_i-\sum _{i=1}^n\bar{X}=0$$

$$\sum _{i=1}^n{x}_i=\sum _{i=1}^n\bar{X}$$

$$\sum _{i=1}^n{x}_i=n\bar{X}$$

$$\sum _{i=1}^n{x}_i=\sum _{i=1}^n{x}_i$$

第六章：概率

原文：statsthinking21.github.io/statsthinking21-core-site/probability.html

译者：飞龙

协议：CC BY-NC-SA 4.0

概率论是处理机会和不确定性的数学分支。它构成了统计学基础的重要部分，因为它为我们提供了描述不确定事件的数学工具。概率的研究部分是由于对理解卡牌或骰子等游戏的兴趣。这些游戏提供了许多统计概念的有用例子，因为当我们重复这些游戏时，不同结果发生的可能性保持（大部分）不变。然而，关于概率含义的深刻问题我们在这里不会讨论；如果您对了解更多有关这个迷人主题及其历史感兴趣，请参阅结尾的建议阅读。

6.1 什么是概率？

非正式地，我们通常将概率视为描述某个事件发生可能性的数字，范围从零（不可能）到一（确定）。有时概率将以百分比的形式表示，范围从零到一百，就像天气预报预测今天下雨的概率为百分之二十一样。在每种情况下，这些数字都表达了该特定事件有多大可能发生，从绝对不可能到绝对确定。

为了形式化概率论，我们首先需要定义一些术语：

• 实验是产生或观察结果的任何活动。例如，抛硬币、掷一个六面骰子，或者尝试一条新的上班路线看看它是否比旧路线更快。

• 样本空间是实验的可能结果的集合。我们通过在一组花括号中列出它们来表示这些结果。对于抛硬币，样本空间是{正面，反面}。对于一个六面骰子，样本空间是可能出现的每个数字：{1,2,3,4,5,6}。对于到达工作地点所需的时间，样本空间是所有可能的实数大于零（因为到达某个地方不可能花费负数的时间，至少目前还不可能）。我们不会尝试在括号内写出所有这些数字。

• 事件是样本空间的子集。原则上，它可以是样本空间中可能结果的一个或多个，但在这里，我们将主要关注基本事件，它们由恰好一个可能结果组成。例如，这可能是在一次抛硬币中获得正面，掷骰子时掷出 4，或者通过新路线回家花费 21 分钟。

现在我们已经有了这些定义，我们可以概述概率的正式特征，这些特征是由俄罗斯数学家安德烈·科尔莫戈洛夫首次定义的。这些是值必须具备的特征，如果它要成为概率的话。假设我们有一个由 N 个独立事件$E_1,E_2,...,E_N$定义的样本空间，$X$是一个随机变量，表示发生了哪个事件。$P(X=E_i)$是事件$i$的概率：

• 概率不能为负数：$P(X=E_i)\ge 0$

• 样本空间中所有结果的总概率为 1；也就是说，如果我们取每个 Ei 的概率并将它们相加，它们必须加起来等于 1。我们可以使用求和符号$\sum$来表示这一点：

  $$\sum _{i=1}^{N}P(X=E_i)=P(X=E_1)+P(X=E_2)+...+P(X=E_N)=1$$

  这被解释为“取所有 N 个基本事件，我们已经从 1 到 N 进行了标记，并将它们的概率相加。它们必须加起来等于一。”

• 任何单个事件的概率都不能大于一：$P(X=E_i)\le 1$。这是由前面的观点所暗示的；因为它们必须加起来等于一，而且它们不能是负数，所以任何特定的概率都不能超过一。

6.2 我们如何确定概率？

既然我们知道了概率是什么，我们如何实际确定任何特定事件的概率呢？

6.2.1 个人信念

假设我问你如果伯尼·桑德斯在 2016 年总统选举中成为民主党提名人而不是希拉里·克林顿，他会赢得选举的概率是多少？我们实际上无法进行实验来找到结果。然而，大多数了解美国政治的人都愿意至少猜测这一事件的概率。在许多情况下，个人知识和/或意见是我们确定事件概率的唯一指南，但这并不是非常科学上令人满意的。

6.2.2 经验频率

确定事件概率的另一种方法是多次进行实验，并计算每个事件发生的频率。从不同结果的相对频率，我们可以计算出每个结果的概率。例如，假设我们想知道旧金山下雨的概率。我们首先必须定义实验 - 假设我们将查看 2017 年每一天的国家气象局数据，并确定在旧金山市中心气象站是否有下雨。根据这些数据，2017 年有 73 天下雨。为了计算旧金山下雨的概率，我们只需将下雨的天数除以计数的天数（365），得出 P（2017 年旧金山下雨）= 0.2。

我们如何知道经验概率给出了正确的数字？这个问题的答案来自于大数定律，它表明随着样本量的增加，经验概率将接近真实概率。我们可以通过模拟大量的硬币抛掷来看到这一点，并在每次抛掷后查看我们对正面概率的估计。我们将在后面的章节中更多地讨论模拟；现在，只需假设我们有一种计算方法来生成每次硬币抛掷的随机结果。

图 6.1 的左侧面板显示，随着样本数量（即，硬币抛掷试验）的增加，正面的估计概率会收敛到 0.5 的真实值。然而，请注意，当样本量较小时，估计值可能与真实值相差甚远。这在 2017 年阿拉巴马州美国参议院特别选举中得到了真实世界的例证，该选举将共和党人罗伊·摩尔对阵民主党人道格·琼斯。图 6.1 的右侧面板显示了在晚上的过程中每个候选人报告的相对选票数量，随着越来越多的选票被计算出来。晚上早些时候，选票数量特别不稳定，从琼斯的大幅领先到摩尔长时间领先，最终琼斯取得领先并赢得了比赛。

左侧：大数定律的演示。硬币被抛掷了 30,000 次，每次抛掷后，根据迄今为止收集到的正反面数量计算出正面的概率。大约需要 15,000 次抛掷，概率才会稳定在真实概率 0.5。右侧：2017 年 12 月 12 日阿拉巴马州参议院特别选举中的选票相对比例，作为报告选区百分比的函数。这些数据是从 https://www.ajc.com/news/national/alabama-senate-race-live-updates-roy-moore-doug-jones/KPRfkdaweoiXICW3FHjXqI/转录的。

图 6.1：左侧：大数定律的演示。硬币被抛掷了 30,000 次，每次抛掷后根据迄今为止收集到的正反面数量计算出正面的概率。大约需要 15,000 次抛掷才能使概率稳定在真实概率 0.5。右侧：2017 年 12 月 12 日阿拉巴马州参议院特别选举中的选票相对比例，作为报告选区百分比的函数。这些数据是从www.ajc.com/news/national/alabama-senate-race-live-updates-roy-moore-doug-jones/KPRfkdaweoiXICW3FHjXqI/转录的。

这两个例子表明，虽然大样本最终会收敛于真实概率，但小样本的结果可能相差甚远。不幸的是，许多人忘记了这一点，并过分解释了小样本的结果。这被心理学家丹尼·卡尼曼和阿莫斯·特沃斯基称为“小数定律”，他们表明人们（甚至是受过训练的研究人员）经常表现得好像大数定律甚至适用于小样本，对基于小数据集的结果给予了过多的信任。在课程中，我们将看到许多例子，说明当统计结果是基于小样本生成时，它们是多么不稳定。

6.2.3 古典概率

我们很少有人会抛掷硬币数万次，但我们仍然愿意相信抛掷正面的概率是 0.5。这反映了我们使用另一种计算概率的方法，我们称之为“古典概率”。在这种方法中，我们根据对情况的了解直接计算概率。

古典概率起源于对骰子和纸牌等游戏的研究。一个著名的例子来自于法国赌徒谢瓦利埃·德梅雷遇到的问题。德梅雷玩了两种不同的骰子游戏：在第一种游戏中，他押注至少有一个六在投掷六面骰子的四次中出现的机会，而在第二种游戏中，他押注至少有一个双六在投掷两个骰子的 24 次中出现的机会。他期望在这两个赌博中赚钱，但他发现，虽然平均上他在第一个赌博中赚了钱，但当他多次玩第二个赌博时，他实际上平均上是赔钱的。为了理解这一点，他求助于他的朋友、数学家布莱兹·帕斯卡，现在他被认为是概率论的创始人之一。

我们如何使用概率论来理解这个问题呢？在古典概率中，我们假设样本空间中的所有基本事件是等可能发生的；也就是说，当你掷骰子时，每种可能的结果（{1,2,3,4,5,6}）都是等可能发生的。（不允许使用偏骰子！）在这种情况下，我们可以计算任何单个结果的概率为 1 除以可能结果的数量：

$$P(outcom{e}_i)=\frac{1}{\text{number of possible outcomes}}$$

对于六面骰子，每个单个结果的概率是 1/6。

这很好，但德梅雷对更复杂的事件感兴趣，比如多次掷骰子会发生什么。我们如何计算复杂事件的概率（这是单个事件的“并集”），比如在第一次或第二次掷骰子时掷出一个六？我们用$\cup$符号在数学上表示事件的并集：例如，如果第一次掷骰子掷出六的概率被称为$P(Roll{6}_{throw1})$，第二次掷骰子掷出六的概率被称为$P(Roll{6}_{throw2})$，那么并集被称为$P(Roll{6}_{throw1}\cup Roll{6}_{throw2})$。

de Méré认为（我们将在下面看到是错误的），他可以简单地将两个事件的概率相加来计算组合事件的概率，这意味着首次或第二次掷出六的概率将如下计算：

$$P(Roll{6}_{throw1})=1/6$$

$$P(Roll{6}_{throw2})=1/6$$

de Méré的错误:

$$P(Roll{6}_{throw1}\cup Roll{6}_{throw2})=P(Roll{6}_{throw1})+P(Roll{6}_{throw2})=1/6+1/6=1/3$$

de Méré基于这个错误的假设推理，即四次掷骰子至少有一个六的概率是每次单独掷骰子的概率之和：$4\ast \frac{1}{6}=\frac{2}{3}$。同样，他推断出，由于掷两个骰子时出现双六的概率是 1/36，那么掷两个骰子 24 次至少出现一次双六的概率将是$24\ast \frac{1}{36}=\frac{2}{3}$。然而，尽管他在第一次赌注上一直赢钱，但在第二次赌注上却输钱了。是什么原因呢？

要理解 de Méré的错误，我们需要介绍一些概率论的规则。第一个是减法规则，它说事件 A 不发生的概率是 1 减去事件发生的概率：

$$P(\neg A)=1-P(A)$$

其中$\neg A$表示“非 A”。这个规则直接源自我们上面讨论的公理；因为 A 和$\neg A$是唯一可能的结果，所以它们的总概率必须加起来为 1。例如，如果单次掷骰子掷出 1 的概率是$\frac{1}{6}$，那么掷出非 1 的概率就是$\frac{5}{6}$。

第二条规则告诉我们如何计算联合事件的概率 - 也就是两个事件都发生的概率。我们称之为交集，用$\cap$符号表示；因此，$P(A\cap B)$表示 A 和 B 都发生的概率。我们将专注于一种规则的版本，该规则告诉我们如何在两个事件彼此独立的特殊情况下计算这个数量；我们稍后将学习独立性概念的确切含义，但现在我们可以认为两次掷骰子是独立事件。我们通过简单地将两个事件的概率相乘来计算两个独立事件的交集的概率：

$$P(A\cap B)=P(A)\ast P(B)\text{当且仅当 A 和 B 是独立的时候}$$

因此，两次掷出六的概率是$\frac{1}{6}\ast \frac{1}{6}=\frac{1}{36}$。

第三条规则告诉我们如何将概率相加 - 就是在这里我们看到了 de Méré的错误来源。加法规则告诉我们，要获得两个事件中任一事件发生的概率，我们将单独的概率相加，然后减去两者同时发生的可能性：

$$P(A\cup B)=P(A)+P(B)-P(A\cap B)$$

从某种意义上说，这阻止我们将这些实例计算两次，这就是这条规则与 de Méré的错误计算有何不同。假设我们想要找到两次掷骰子中至少掷出 6 的概率。根据我们的规则：

$$P(Roll{6}_{throw1}\cup Roll{6}_{throw2})=P(Roll{6}_{throw1})+P(Roll{6}_{throw2})-P(Roll{6}_{throw1}\cap Roll{6}_{throw2})$$

$$=\frac{1}{6}+\frac{1}{6}-\frac{1}{36}=\frac{11}{36}$$

图 6.2：此矩阵中的每个单元格代表掷骰子两次的一个结果，列代表第一次掷骰子，行代表第二次掷骰子。红色表示第一次或第二次掷出六的单元格；其余显示为蓝色。

让我们使用图形描述来对这个规则有一个不同的视角。图 6.2 显示了表示两次投掷中所有可能结果组合的矩阵，并突出显示了涉及第一次或第二次投掷中的六的单元格。如果你数一数红色的单元格，你会发现有 11 个这样的单元格。这说明了为什么加法规则给出了与 de Méré不同的答案；如果我们像他一样简单地将两次投掷的概率相加，那么我们会将(6,6)计算两次，而实际上它只应该计算一次。

6.2.4 解决 de Méré的问题

Blaise Pascal 利用概率规则解决了 de Méré的问题。首先，他意识到计算至少一个事件的概率组合是棘手的，而计算某事在多个事件中不发生的概率相对容易——它只是各个事件概率的乘积。因此，他不是计算四次投掷中至少出现一个六的概率，而是计算所有投掷中没有六的概率：

$$P(\text{四次投掷中没有六})=\frac{5}{6}\ast \frac{5}{6}\ast \frac{5}{6}\ast \frac{5}{6}=(\frac{5}{6}{)}^4=0.482$$

然后他利用四次投掷中没有六的概率是至少有一个六的概率的补集（因此它们必须相加为一），并使用减法规则计算感兴趣的概率：

$$P(\text{四次投掷中至少有一个六})=1-(\frac{5}{6}{)}^4=0.517$$

de Méré打赌他在四次投掷中至少会掷出一个六的概率大于 0.5，这解释了为什么 de Méré平均赚钱。

但是 de Méré的第二次赌注呢？Pascal 使用了同样的技巧：

$$P(\text{24 次投掷中没有双六})=(\frac{35}{36}{)}^{24}=0.509$$

$$P(\text{24 次投掷中至少有一个双六})=1-(\frac{35}{36}{)}^{24}=0.491$$

这种结果的概率略低于 0.5，说明了为什么 de Méré在这个赌注上平均亏钱。

6.3 概率分布

概率分布描述了实验中所有可能结果的概率。例如，2018 年 1 月 20 日，篮球运动员斯蒂芬·库里在对休斯顿火箭队的比赛中只投中了 4 次罚球中的 2 次。我们知道库里整个赛季罚球的概率是 0.91，所以他在一场比赛中只投中 50%的罚球似乎是不太可能的，但确切有多少可能性呢？我们可以使用理论概率分布来确定这一点；在本书中，我们将遇到许多这些概率分布，每个都适合描述不同类型的数据。在这种情况下，我们使用二项式分布，它提供了一种计算在每次试验中成功或失败的情况下，某些成功次数的概率的方法，给定每次试验上的已知成功概率（称为“伯努利试验”）。这个分布被定义为：

$$P(k;n,p)=P(X=k)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p^k(1-p{)}^{n-k}$$

这指的是在概率为 p 的情况下，在 n 次试验中出现 k 次成功的概率。你可能不熟悉$\left(\genfrac{}{}{0ex}{}{n}{k}\right)$，它被称为二项式系数。二项式系数也被称为“n 选 k”，因为它描述了从 n 个总项中选择 k 个项的不同方式的数量。二项式系数计算如下：

$$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n!}{k!(n-k)!}$$

其中感叹号（!）表示数字的阶乘：

$$n!=\prod _{i=1}^{n}i=n\ast (n-1)\ast ...\ast 2\ast 1$$

乘积运算符$\prod$类似于求和运算符$\sum$，只是它是相乘而不是相加。在这种情况下，它将从一到$n$的所有数字相乘在一起。

在斯蒂芬·库里罚球的例子中：

$$P(2;4,0.91)=\left(\genfrac{}{}{0ex}{}{4}{2}\right)0.91^2(1-0.91{)}^{4-2}=0.040$$

这表明，鉴于库里的整体罚球命中率，他在 4 次罚球中只命中 2 次的概率是非常低的。这只是表明在现实世界中不太可能的事情实际上确实会发生。

6.3.1 累积概率分布

通常我们不仅想知道特定值有多大可能性，还想知道找到一个与特定值一样极端或更极端的值有多大可能性；当我们在第 9 章讨论假设检验时，这将变得非常重要。为了回答这个问题，我们可以使用累积概率分布；标准概率分布告诉我们某个特定值的概率，而累积分布告诉我们一个与某个特定值一样大或更大（或者一样小或更小）的值的概率。

在罚球的例子中，我们可能想知道：鉴于库里的整体罚球概率为 0.91，斯蒂芬·库里在四次尝试中命中 2 次或更少罚球的概率是多少。为了确定这一点，我们可以简单地使用二项概率方程，并将所有可能的 k 值代入并相加。

$$P(k\le 2)=P(k=2)+P(k=1)+P(k=0)=6e^{-5}+.002+.040=.043$$

在许多情况下，可能结果的数量对我们来说太大，无法通过枚举所有可能的值来计算累积概率；幸运的是，它可以直接计算任何理论概率分布。表 6.1 显示了上面示例中每个成功罚球次数的累积概率，从中我们可以看到库里在 4 次尝试中命中 2 次或更少罚球的概率为 0.043。

表 6.1：斯蒂芬·库里在 4 次尝试中成功罚球次数的简单和累积概率分布。

成功数量	概率	累积概率
0	0.000	0.000
1	0.003	0.003
2	0.040	0.043
3	0.271	0.314
4	0.686	1.000

6.4 条件概率

到目前为止，我们只限制在简单概率上 - 也就是单个事件或事件组合的概率。然而，我们经常希望确定某个事件发生的概率，假设发生了另一个事件，这被称为条件概率。

让我们以 2016 年美国总统选举为例。有两个简单的概率可以用来描述选民。首先，我们知道美国选民与共和党有关的概率：$p(共和党)=0.44$。我们还知道投票支持唐纳德·特朗普的选民的概率：$p(特朗普选民)=0.46$。然而，假设我们想知道以下内容：一个人投票支持唐纳德·特朗普的概率是多少，假设他们是共和党人？

要计算给定 B 的条件概率 A（我们将其写为$P(A|B)$，“给定 B 的 A 的概率”），我们需要知道联合概率（即 A 和 B 同时发生的概率）以及 B 的整体概率：

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

也就是说，我们想知道在被条件限制的情况下，两件事情都是真的概率。

图 6.3：条件概率的图形描述，显示了条件概率如何将我们的分析限制在数据的子集中。

以图形方式思考这点可能会有所帮助。图 6.3 显示了一个流程图，描述了选民的整体人口是如何分为共和党人和民主党人的，并且条件概率（以政党为条件）如何进一步根据他们的投票将每个政党的成员细分。

6.5 从数据计算条件概率

我们还可以直接从数据中计算条件概率。假设我们对以下问题感兴趣：一个人患有糖尿病的概率是多少，假设他们不活跃？即，$P(糖尿病|不活跃)$。NHANES 数据集包括两个变量，涉及这个问题的两个部分。第一个（糖尿病）询问这个人是否被告知他们患有糖尿病，第二个（身体活动）记录这个人是否参加至少中等强度的体育、健身或娱乐活动。让我们首先计算简单概率，如表 6.2 所示。表格显示 NHANES 数据集中有糖尿病的人的概率为 0.1，不活跃的人的概率为 0.45。

表 6.2：糖尿病和体力活动的摘要数据

答案	无糖尿病	糖尿病概率	无身体活动	身体活动概率
否	4893	0.9	2472	0.45
是	550	0.1	2971	0.55

表 6.3：糖尿病和身体活动变量的联合概率。

糖尿病	身体活动	n	概率
否	否	2123	0.39
否	是	2770	0.51
是	否	349	0.06
是	是	201	0.04

要计算 $P(糖尿病|不活跃)$ ，我们还需要知道患糖尿病和不活跃的联合概率，除了每个简单概率。这些显示在表 6.3 中。根据这些联合概率，我们可以计算 $P(糖尿病|不活跃)$。在计算机程序中，一种方法是首先确定每个个体的 PhysActive 变量是否等于“否”，然后取这些真值的平均值。由于大多数编程语言（包括 R 和 Python）将 TRUE/FALSE 值分别视为 1/0，这使我们可以通过简单地取表示其真值的逻辑变量的平均值来轻松识别简单事件的概率。然后我们使用该值来计算条件概率，从中我们发现，患糖尿病的人在身体不活跃的情况下的概率为 0.141。

6.6 独立性

“独立”这个术语在统计学中有一个非常具体的含义，与常规用法略有不同。两个变量之间的统计独立意味着知道一个变量的值不会告诉我们关于另一个变量的值的任何信息。这可以表示为：

$$P(A|B)=P(A)$$

也就是说，给定 B 的某个值时 A 的概率与 A 的整体概率是一样的。从这个角度来看，我们发现在现实世界中许多我们称之为“独立”的情况实际上并不是统计上独立的。例如，加利福尼亚州的一小部分公民目前正在推动宣布一个名为杰斐逊的新独立州，该州将包括加利福尼亚州北部和俄勒冈州的一些县。如果这种情况发生，那么当前加利福尼亚居民现在居住在杰斐逊州的概率将是 $P(\text{杰斐逊人})=0.014$，而他们仍然是加利福尼亚居民的概率将是 $P(\text{加利福尼亚人})=0.986$。新的州可能在政治上是独立的，但它们不在统计上是独立的，因为如果我们知道一个人是杰斐逊人，那么我们可以肯定他们不是加利福尼亚人！也就是说，尽管在日常语言中，“独立”通常指的是互斥的集合，但统计独立是指一个变量的值无法从另一个变量的值预测出来的情况。例如，知道一个人的头发颜色不太可能告诉你他们更喜欢巧克力还是草莓冰淇淋。

让我们看另一个例子，使用 NHANES 数据：身体健康和心理健康是否彼此独立？NHANES 包括两个相关问题：PhysActive，询问个体是否进行身体活动，以及DaysMentHlthBad，询问个体在过去 30 天中有多少天经历了糟糕的心理健康。让我们考虑在过去一个月中有超过 7 天糟糕心理健康的人。基于此，我们可以定义一个名为badMentalHealth的新变量，作为一个逻辑变量，告诉每个人是否有超过 7 天的糟糕心理健康。我们可以首先总结数据，显示有多少个体落入两个变量的每种组合（在表 6.4 中显示），然后除以总观察数，创建一个比例表（在表 6.5 中显示）：

表 6.4：心理健康和身体活动的绝对频率数据总结。

身体活动	心理不健康	心理健康	总数
No	414	1664	2078
Yes	292	1926	2218
Total	706	3590	4296

表 6.5：心理健康和身体活动的相对频率数据总结。

身体活动	心理不健康	心理健康	总数
No	0.10	0.39	0.48
Yes	0.07	0.45	0.52
Total	0.16	0.84	1.00

这显示了所有观察结果中落入每个单元格的比例。然而，我们想要知道的是这里的条件概率，即取决于是否进行身体活动的糟糕心理健康的条件概率。为了计算这个，我们将每个身体活动组除以其总观察数，使得每行现在总和为 1（在表 6.6 中显示）。在这里，我们看到了每个身体活动组的糟糕或良好心理健康的条件概率（在前两行中），以及第三行中的总体糟糕或良好心理健康的概率。要确定心理健康和身体活动是否独立，我们将比较糟糕心理健康的简单概率（第三行）与在进行身体活动的情况下糟糕心理健康的条件概率（第二行）。

表 6.6：给定身体活动的条件概率总结。

身体活动	心理不健康	心理健康	总数
No	0.20	0.80	1
Yes	0.13	0.87	1
Total	0.16	0.84	1

糟糕心理健康的总体概率$P(\text{bad mental health})$为 0.16，而条件概率$P(\text{bad mental health|physically active})$为 0.13。因此，似乎条件概率略小于总体概率，这表明它们不是独立的，尽管我们不能仅凭数字就确定，因为这些数字可能由于样本中的随机变异而不同。本书后面我们将讨论统计工具，让我们直接测试两个变量是否独立。

6.7 反转条件概率：贝叶斯定理

在许多情况下，我们知道$P(A|B)$，但我们真正想知道的是$P(B|A)$。这在医学筛查中经常发生，我们知道$P(\text{疾病|阳性检测结果})$，但我们想知道的是$P(\text{阳性检测结果|疾病})$。例如，一些医生建议 50 岁以上的男性接受一种名为前列腺特异抗原（PSA）的检测，以筛查可能的前列腺癌。在一项测试被批准用于医学实践之前，制造商需要测试测试性能的两个方面。首先，他们需要展示它的敏感性 - 也就是说，当疾病存在时发现疾病的可能性有多大：$\text{敏感性}=P(\text{疾病|阳性检测})$。他们还需要展示它的特异性：也就是说，在没有疾病的情况下给出阴性结果的可能性有多大：$\text{特异性}=P(\text{无疾病|阴性检测})$。对于 PSA 测试，我们知道敏感性约为 80%，特异性约为 70%。然而，这些并不能回答医生想要为任何特定患者回答的问题：在检测结果呈阳性的情况下，他们实际上患癌症的可能性有多大？这要求我们反转定义敏感性的条件概率：我们想知道的不是$P(阳性检测|疾病)$，而是$P(疾病|阳性检测)$。

为了反转条件概率，我们可以使用贝叶斯定理：

$$P(B|A)=\frac{P(A|B)\ast P(B)}{P(A)}$$

贝叶斯定理相当容易推导出来，基于我们在本章早些时候学到的概率规则（有关此推导，请参阅附录）。

如果我们只有两个结果，我们可以使用总和规则重新定义$P(A)$来更清晰地表达贝叶斯定理：

$$P(A)=P(A|B)\ast P(B)+P(A|\neg B)\ast P(\neg B)$$

利用这一点，我们可以重新定义贝叶斯定理：

$$P(B|A)=\frac{P(A|B)\ast P(B)}{P(A|B)\ast P(B)+P(A|\neg B)\ast P(\neg B)}$$

我们可以将相关数字代入这个方程中，以确定一个 PSA 检测结果呈阳性的个体实际上患癌症的可能性 - 但请注意，为了做到这一点，我们还需要知道该人群患癌症的总体概率，我们通常称之为基础率。让我们以一个 60 岁的男性为例，他在接下来的 10 年内患前列腺癌的概率为$P(癌症)=0.058$。使用我们上面概述的敏感性和特异性值，我们可以计算个体在检测结果呈阳性的情况下患癌症的可能性：

$$P(\text{癌症|检测})=\frac{P(\text{检测|癌症})\ast P(\text{癌症})}{P(\text{检测|癌症})\ast P(\text{癌症})+P(\text{检测|}\neg \text{癌症})\ast P(\neg \text{癌症})}$$

$$=\frac{0.8\ast 0.058}{0.8\ast 0.058+0.3\ast 0.942}=0.14$$

这相当小 - 你觉得这让人惊讶吗？许多人确实如此，事实上有大量的心理学文献表明人们在判断中系统地忽视基础率（即总体患病率）。

6.8 从数据中学习

另一种思考贝叶斯定理的方式是作为一种根据数据更新我们对世界的信念的方式 - 也就是说，利用数据来了解世界。让我们再次看看贝叶斯定理：

$$P(B|A)=\frac{P(A|B)\ast P(B)}{P(A)}$$

贝叶斯定理的不同部分有特定的名称，与它们在使用贝叶斯定理更新我们的信念中的作用有关。我们首先对 B 的概率有一个初始猜测（$P(B)$），我们称之为先验概率。在 PSA 示例中，我们使用基础率作为先验，因为这是我们在知道测试结果之前对个体患癌症机会的最佳猜测。然后我们收集一些数据，在我们的例子中是测试结果。数据 A 与结果 B 一致的程度由$P(A|B)$给出，我们称之为似然性。你可以把它看作是在特定假设为真的情况下，数据有多大可能性。在我们的例子中，被测试的假设是个体是否患有癌症，似然性是基于我们对测试敏感性的了解（即，给定癌症存在的情况下测试呈阳性的概率）。分母（$P(A)$）被称为边际似然性，因为它表达了数据的整体可能性，平均分布在 B 的所有可能值上（在我们的例子中是疾病存在和疾病不存在）。左边的结果（$P(B|A)$）被称为后验 - 因为它是计算的最终结果。

还有另一种写贝叶斯定理的方式，使得这一点更加清晰：

$$P(B|A)=\frac{P(A|B)}{P(A)}\ast P(B)$$

左边的部分（$\frac{P(A|B)}{P(A)}$）告诉我们，相对于数据的整体（边际）概率，数据 A 在给定 B 的情况下更可能或更不可能发生，而右边的部分（$P(B)$）告诉我们，在我们对数据一无所知之前，我们认为 B 有多大可能性。这使得更清楚，贝叶斯定理的作用是根据数据在给定 B 的情况下比整体更可能发生的程度来更新我们的先验知识。如果假设在给定数据的情况下更可能发生，那么我们会增加对假设的信念；如果在给定数据的情况下更不可能发生，那么我们会减少对假设的信念。

6.9 赔率和赔率比

上一节的结果显示，基于阳性 PSA 测试结果，个体患癌症的可能性仍然相当低，尽管比我们知道测试结果之前大两倍。我们经常希望更直接地量化概率之间的关系，这可以通过将它们转换为赔率来实现，赔率表达了某件事发生或不发生的相对可能性：

$$\text{A 的赔率}=\frac{P(A)}{P(\neg A)}$$

在我们的 PSA 示例中，患癌症的赔率（给定阳性测试）为：

$$\text{癌症的赔率}=\frac{P(\text{癌症})}{P(\neg \text{癌症})}=\frac{0.14}{1-0.14}=0.16$$

这告诉我们，即使测试呈阳性，患癌症的赔率也相当低。作为对比，单次掷骰子出现 6 的赔率为：

$$\text{赔率为 6}=\frac{1}{5}=0.2$$

顺便说一句，这就是为什么许多医学研究人员越来越谨慎地使用广泛的筛查测试来检测相对不常见的疾病的原因；大多数阳性结果最终都会被证明是假阳性，导致不必要的后续测试可能会出现并发症，更不用说给患者增加的压力了。

我们还可以使用赔率来比较不同的概率，通过计算所谓的赔率比 - 这正是它的名字。例如，假设我们想知道阳性测试如何增加个体患癌症的赔率。我们可以首先计算先验赔率 - 也就是，在我们知道这个人测试呈阳性之前的赔率。这些是使用基础率计算的：

$$\text{先验赔率}=\frac{P(\text{癌症})}{P(\neg \text{癌症})}=\frac{0.058}{1-0.058}=0.061$$

然后我们可以将这些与后验赔率进行比较，后验赔率是使用后验概率计算的：

$$\text{赔率比}=\frac{\text{后验赔率}}{\text{先验赔率}}=\frac{0.16}{0.061}=2.62$$

这告诉我们，给出阳性检测结果，患癌症的几率增加了 2.62 倍。赔率比是我们后来将称之为效应大小的一个例子，它是量化任何特定统计效应相对大小的一种方式。

6.10 概率是什么意思？

你可能会觉得谈论一个人患癌症的概率取决于检测结果有点奇怪；毕竟，一个人要么患癌症，要么不患。在历史上，概率有两种不同的解释方式。第一种（称为频率解释）是根据长期频率解释概率。例如，在抛硬币的情况下，它将反映在大量抛掷后长期内正面的相对频率。虽然这种解释对于可以重复多次的事件（如抛硬币）可能是有意义的，但对于只会发生一次的事件（如个人的生活或特定的总统选举）就不那么合理了；正如经济学家约翰·梅纳德·凯恩斯所说，“从长远来看，我们都会死去。”

概率的另一种解释（称为贝叶斯解释）是对特定命题的信念程度。如果我问你“美国在 2040 年前返回月球的可能性有多大”，你可以根据你的知识和信念回答这个问题，即使没有相关频率来计算频率概率。我们经常表达主观概率的一种方式是根据一个人愿意接受特定赌注的程度。例如，如果你认为美国在 2040 年前登月的概率是 0.1（即 9 比 1 的赔率），那意味着如果事件发生，你应该愿意接受任何超过 9 比 1 赔率的赌注。

正如我们将看到的，概率的这两种不同定义与统计学家在测试统计假设时所考虑的两种不同方式非常相关，我们将在后面的章节中遇到。

6.11 学习目标

阅读完本章后，你应该能够：

• 描述所选随机实验的样本空间。

• 计算给定事件集的相对频率和经验概率

• 计算单个事件、互补事件以及事件集合的并集和交集的概率。

• 描述大数定律。

• 描述概率和条件概率之间的差异

• 描述统计独立的概念

• 使用贝叶斯定理计算逆条件概率。

6.12 建议阅读

• 《醉汉的漫步：随机性如何统治我们的生活》，作者 Leonard Mlodinow

• 《关于机会的十大伟大思想》，作者 Persi Diaconis 和 Brian Skyrms

6.13 附录

6.13.1 贝叶斯规则的推导

首先，记住计算条件概率的规则：

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

我们可以重新排列这个公式，得到使用条件概率计算联合概率的公式：

$$P(A\cap B)=P(A|B)\ast P(B)$$

利用这个公式，我们可以计算逆概率：

$$P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{P(A|B)\ast P(B)}{P(A)}$$

第七章：采样

原文：statsthinking21.github.io/statsthinking21-core-site/sampling.html

译者：飞龙

协议：CC BY-NC-SA 4.0

统计学中的一个基本思想是，我们可以根据人口的一个相对较小的样本对整个人口进行推断。在本章中，我们将介绍统计抽样的概念，并讨论为什么它有效。

在美国生活的任何人都会熟悉从政治民意调查中抽样的概念，这已经成为我们选举过程的核心部分。在某些情况下，这些民意调查可以非常准确地预测选举结果。最著名的例子来自 2008 年和 2012 年的美国总统选举，民意调查员内特·西尔弗（Nate Silver）在 2008 年正确预测了 49/50 个州的选举结果，在 2012 年预测了所有 50 个州的选举结果。西尔弗通过结合来自 21 个不同民意调查的数据来做到这一点，这些民意调查在倾向于共和党或民主党的程度上有所不同。每个民意调查包括大约 1000 名可能的选民的数据 - 这意味着西尔弗几乎可以准确预测超过 1.25 亿选民的选票模式，只使用了大约 2.1 万人的数据，以及其他知识（比如这些州过去的投票情况）。

7.1 我们如何进行抽样？

我们在采样中的目标是确定感兴趣的整个人口的统计量的值，只使用人口的一个小子集。我们主要这样做是为了节省时间和精力 - 当只需要一个小样本就足以准确估计感兴趣的统计量时，为什么要费劲测量人口中的每个个体呢？

在选举的例子中，人口是被调查地区的所有注册选民，样本是由民意调查组织选出的 1000 个个体。我们选择样本的方式对确保样本代表整个人口至关重要，这是统计抽样的主要目标。很容易想象一个非代表性的样本；如果民意调查员只打电话给他们从当地民主党那里得到的名单上的人，那么调查结果很可能不代表整个人口。一般来说，我们会定义代表性调查为每个人口成员被选中的机会相等。当这种情况失败时，我们就需要担心我们在样本上计算的统计量是否有偏 - 也就是说，它的值是否与人口值（我们称之为参数）有系统性的不同。请记住，我们通常不知道这个人口参数，因为如果我们知道的话，我们就不需要抽样了！但我们将使用一些例子来解释一些关键的思想，其中我们可以访问整个人口。

重要的是要区分两种不同的采样方式：有放回和无放回。在有放回采样中，从人口中抽取一个成员后，将其放回池中，这样他们有可能再次被抽样。在无放回采样中，一旦成员被抽样，他们就不再有资格被再次抽样。最常见的是使用无放回采样，但在某些情况下，我们会使用有放回采样，比如在第 8 章中讨论的一种叫做自助法的技术。

7.2 采样误差

无论我们的样本有多具代表性，我们计算出的统计量与人口参数至少略有不同的可能性很大。我们称之为抽样误差。如果我们抽取多个样本，我们的统计估计值的值也会因样本而异；我们将这个统计量在样本中的分布称为抽样分布。

抽样误差与我们对人口的测量质量直接相关。显然，我们希望从样本中获得的估计值尽可能接近人口参数的真实值。然而，即使我们的统计量是无偏的（也就是说，我们期望它具有与人口参数相同的值），任何特定估计值的值都将与人口值不同，并且当抽样误差更大时，这些差异将更大。因此，减少抽样误差是更好地测量的重要一步。

我们将以 NHANES 数据集为例；我们将假设 NHANES 数据集是感兴趣的整个人口，然后我们将从该人口中抽取随机样本。在下一章中，我们将更多地讨论计算机中“随机”样本生成的工作原理。

在这个例子中，我们知道成年人口的均值（168.35）和身高的标准差（10.16），因为我们假设 NHANES 数据集是人口。表 7.1 显示了从 NHANES 人口中抽取的 50 个个体的几个样本计算出的统计数据。

表 7.1：NHANES 身高变量的几个样本的均值和标准差示例。

样本均值	样本标准差
167	9.1
171	8.3
170	10.6
166	9.5
168	9.5

样本均值和标准差与人口值相似，但并非完全相等。现在让我们抽取 50 个个体的大量样本，计算每个样本的均值，并查看得到的均值的抽样分布。我们必须决定抽取多少样本才能很好地估计抽样分布 - 在这种情况下，我们将抽取 5000 个样本，以便我们对答案非常有信心。请注意，像这样的模拟有时可能需要几分钟才能运行，并且可能会使您的计算机变得吃力。图 7.1 中的直方图显示，对于 50 个个体的每个样本估计的均值有些变化，但总体上它们都集中在人口均值周围。5000 个样本均值的平均值（168.3463）非常接近真实的人口均值（168.3497）。

图 7.1：蓝色直方图显示了从 NHANES 数据集中随机抽取的 5000 个样本的均值的抽样分布。灰色直方图是完整数据集的参考。

7.3 均值的标准误差

在本书的后面，能够描述我们的样本有多么变化是至关重要的，以便对样本统计量进行推断。对于均值，我们使用一个称为均值的标准误差（SEM）的量来做到这一点，可以将其视为均值的抽样分布的标准差。要计算我们样本的均值的标准误差，我们将估计的标准偏差除以样本大小的平方根：

$$SEM=\frac{\hat{\sigma }}{\sqrt{n}}$$

请注意，如果我们的样本很小（大约小于 30），在使用估计标准偏差计算 SEM 时必须小心。

因为我们从 NHANES 人口中有许多样本，并且我们实际上知道人口 SEM（通过将人口标准差除以人口大小计算），我们可以确认使用人口参数（1.44）计算的 SEM 非常接近我们从 NHANES 数据集中抽取的样本的均值的观察标准差（1.43）。

均值标准误差的公式意味着我们的测量质量涉及两个量：总体变异性和样本大小。因为样本大小是 SEM 公式中的分母，所以在保持总体变异性恒定时，较大的样本大小将产生较小的 SEM。我们无法控制总体变异性，但我们可以控制样本大小。因此，如果我们希望改善样本统计数据（通过减少抽样变异性），那么我们应该使用更大的样本。然而，该公式还告诉我们关于统计抽样的一个非常基本的事实，即较大样本的效用随着样本大小的平方根而减小。这意味着加倍样本大小不会使统计数据的质量加倍，而是会使其提高$\sqrt{2}$倍。在10.3 节中，我们将讨论统计功效，这与这个想法密切相关。

7.4 中心极限定理

中心极限定理告诉我们，随着样本大小的增大，均值的抽样分布将变得正态分布，即使每个样本内的数据不是正态分布。

首先，让我们简单介绍一下正态分布。它也被称为高斯分布，以数学家卡尔·弗里德里希·高斯命名，他并没有发明它，但在其发展中起了一定作用。正态分布用两个参数描述：均值（可以认为是峰值的位置）和标准差（指定分布的宽度）。分布的钟形外观永远不会改变，只有其位置和宽度会改变。正态分布在现实世界中收集的数据中经常观察到，正如我们在第 3 章中已经看到的那样，中心极限定理为我们解释了为什么会发生这种情况。

为了看到中心极限定理的作用，让我们使用 NHANES 数据集中的变量 AlcoholYear，该变量呈高度偏斜，如图 7.2 的左面板所示。这个分布，缺乏更好的词来形容，有点奇怪，绝对不是正态分布。现在让我们看看这个变量的均值抽样分布。图 7.2 显示了这个变量的均值抽样分布，通过反复从 NHANES 数据集中抽取大小为 50 的样本并取均值获得。尽管原始数据明显不是正态分布，但抽样分布与正态分布非常接近。

图 7.2：左图：NHANES 数据集中变量 AlcoholYear 的分布，反映了个体一年内饮酒的天数。右图：NHANES 数据集中 AlcoholYear 的均值抽样分布，通过从 NHANES 数据集中重复抽取大小为 50 的样本获得，用蓝色表示。具有相同均值和标准差的正态分布用红色表示。

中心极限定理对统计学很重要，因为它允许我们安全地假设平均数的抽样分布在大多数情况下是正态的。这意味着我们可以利用假设正态分布的统计技术，正如我们将在下一节中看到的那样。它也很重要，因为它告诉我们为什么正态分布在现实世界中如此普遍；每当我们将许多不同因素合并成一个单一数字时，结果很可能是正态分布。例如，任何成年人的身高取决于他们的遗传和经验的复杂混合；即使这些个体贡献可能不是正态分布的，当我们将它们结合起来时，结果就是正态分布。

7.5 学习目标

阅读完本章后，您应该能够：

• 区分总体和样本，以及总体参数和样本统计量

• 描述抽样误差和抽样分布的概念

• 计算平均数的标准误差

• 描述中心极限定理如何决定平均数的抽样分布的性质

7.6 建议阅读

• 《信号与噪音：为什么这么多预测失败-但有些不会》，作者：内特·席尔瓦

第八章：重采样和模拟

原文：statsthinking21.github.io/statsthinking21-core-site/resampling-and-simulation.html

译者：飞龙

协议：CC BY-NC-SA 4.0

计算机模拟的使用已经成为现代统计学的一个重要方面。例如，实际计算机科学中最重要的书之一，名为《数值方法》，说：

“如果让我们选择掌握五英尺高的分析统计书籍和在执行统计蒙特卡洛模拟方面具有一般能力之间，我们肯定会选择后者的技能。”

在本章中，我们将介绍蒙特卡洛模拟的概念，并讨论如何使用它进行统计分析。

8.1 蒙特卡洛模拟

蒙特卡洛模拟的概念是由数学家斯坦·乌拉姆和尼古拉斯·梅特罗波利斯提出的，他们正在为美国曼哈顿计划的原子武器开发工作。他们需要计算中子在物质中与原子核碰撞之前的平均距离，但他们无法使用标准数学计算。乌拉姆意识到这些计算可以使用随机数来模拟，就像赌场游戏一样。在赌场游戏中，例如轮盘赌，数字是随机生成的；为了估计特定结果的概率，可以玩数百次游戏。乌拉姆的叔叔曾在摩纳哥的蒙特卡洛赌场赌博，这显然是这种新技术的名称来源。

执行蒙特卡洛模拟有四个步骤：

1. 定义可能值的域

2. 从概率分布中生成该域内的随机数

3. 使用随机数进行计算

4. 在许多重复中结合结果

例如，假设我想弄清楚为课堂测验留多少时间。我们暂时假设我们知道测验完成时间的分布是正态分布，均值为 5 分钟，标准差为 1 分钟。在这种情况下，测试时间需要多长，以便我们预计所有学生 99%的时间都能完成考试？解决这个问题有两种方法。第一种是使用称为极值统计的数学理论计算答案。然而，这涉及复杂的数学。或者，我们可以使用蒙特卡洛模拟。为此，我们需要从正态分布中生成随机样本。

8.2 统计学中的随机性

“随机”一词在口语中经常用来指称奇怪或意外的事物，但在统计学中，这个词有一个非常具体的含义：如果一个过程是随机的，那么它是不可预测的。例如，如果我抛一枚公平的硬币 10 次，一次抛硬币的结果的值并不能提供任何信息，让我能够预测下一次抛硬币的结果。重要的是要注意，某事是不可预测的并不一定意味着它不是确定性的。例如，当我们抛硬币时，抛硬币的结果是由物理定律决定的；如果我们以足够详细的方式知道所有条件，我们应该能够预测抛硬币的结果。然而，许多因素结合在一起，使得硬币抛掷的结果在实践中是不可预测的。

心理学家已经证明，人类实际上对随机性有相当糟糕的感觉。首先，我们倾向于在不存在的情况下看到模式。在极端情况下，这导致了错觉现象，即人们会在随机模式中看到熟悉的物体（例如将云看作人脸或在一片面包上看到圣母玛利亚）。其次，人类倾向于认为随机过程是自我纠正的，这使我们期望在游戏中输了很多轮之后“应该赢了”，这种现象被称为“赌徒谬误”。

8.3 生成随机数

运行蒙特卡洛模拟需要生成随机数。生成真正的随机数（即完全不可预测的数）只能通过物理过程来实现，例如原子衰变或掷骰子，这些过程很难获得和/或太慢，以至于对于计算机模拟来说不实用（尽管可以从NIST 随机性信标获得）。

通常情况下，我们使用计算机算法生成的伪随机数，而不是真正的随机数；这些数字在某种意义上看起来是随机的，因为它们很难预测，但实际上数字序列会在某个时候重复。例如，在 R 中使用的随机数生成器在$2^{19937}-1$个数字后会重复。这远远超过了宇宙历史上的秒数，我们普遍认为这对于统计分析的大多数目的来说是可以接受的。

大多数统计软件包括用于生成每个主要概率分布的随机数的函数，例如均匀分布（0 到 1 之间的所有值均等）、正态分布和二项分布（例如掷骰子、抛硬币）。图 8.1 显示了从均匀分布和正态分布函数生成的数字的示例。

图 8.1：从均匀（左）或正态（右）分布生成的随机数示例。

我们还可以使用分布的分位数函数生成任何分布的随机数。这是累积分布函数的反函数；分位数函数不是为一组值确定累积概率，而是为一组累积概率确定值。使用分位数函数，我们可以从均匀分布中生成随机数，然后通过其分位数函数将其映射到感兴趣的分布中。

在统计软件中，默认情况下，随机数生成器每次运行时都会生成不同的随机数集。然而，也可以通过将所谓的随机种子设置为特定值来生成完全相同的随机数集。如果你看一下生成这些图表的代码，我们将在本书的许多示例中这样做，以确保这些示例是可重现的。

8.4 使用蒙特卡洛模拟

让我们回到我们的考试完成时间的例子。假设我进行了三次测验，并记录了每个学生对每次考试的完成时间，这可能看起来像图 8.2 中呈现的分布。

图 8.2：模拟完成时间分布。

为了回答我们的问题，我们真正想知道的不是完成时间的分布是什么样子，而是每次测验的最长完成时间的分布是什么样子。为了做到这一点，我们可以模拟测验的完成时间，使用上面提到的完成时间分布正态分布的假设；对于这些模拟的测验中，我们记录最长的完成时间。我们重复这个模拟很多次（5000 次应该足够），并记录完成时间的分布，如图 8.3 所示。

图 8.3：模拟中最长完成时间的分布。

这表明完成时间分布的第 99 百分位数为 8.74，这意味着如果我们给予这么多时间来做测验，那么 99%的时间每个人都应该能完成。重要的是要记住我们的假设很重要 - 如果它们是错误的，那么模拟的结果就毫无意义。在这种情况下，我们假设完成时间分布是正态分布的，具有特定的平均值和标准差；如果这些假设是不正确的（几乎肯定是不正确的，因为经过的时间很少是正态分布的），那么真实的答案可能会大不相同。

8.5 使用模拟进行统计：bootstrap

到目前为止，我们已经使用模拟来演示统计原理，但我们也可以使用模拟来回答真实的统计问题。在本节中，我们将介绍一个称为bootstrap的概念，它让我们可以使用模拟来量化我们对统计估计的不确定性。在课程的后面，我们将看到其他例子，说明模拟通常可以用来回答统计问题，特别是当理论统计方法不可用或者它们的假设太难满足时。

8.5.1 计算 bootstrap

在上一章中，我们利用对平均值的抽样分布的了解来计算平均值的标准误差。但是，如果我们不能假设估计值是正态分布的，或者我们不知道它们的分布是什么怎么办？bootstrap 的想法是使用数据本身来估计答案。这个名字来源于一个拉自己的靴带的想法，表达了我们没有任何外部杠杆的想法，所以我们必须依靠数据本身。bootstrap 方法是由斯坦福大学统计系的 Bradley Efron 构想的，他是世界上最有影响力的统计学家之一。

bootstrap 背后的想法是我们反复从实际数据集中抽样；重要的是，我们进行有放回的抽样，这样同一个数据点往往会在一个样本中被多次表示。然后我们计算我们感兴趣的统计量在每个 bootstrap 样本上，然后使用这些估计值的分布作为我们的抽样分布。在某种意义上，我们将我们特定的样本视为整个人口，然后反复进行有放回的抽样来生成我们用于分析的样本。这假设我们特定的样本是人口的准确反映，对于较大的样本来说可能是合理的，但在样本较小时可能会失效。

让我们首先使用 bootstrap 来估计 NHANES 数据集中成年人身高的平均值的抽样分布，以便我们可以将结果与我们之前讨论的平均标准误差（SEM）进行比较。

图 8.4：使用 bootstrap 来计算 NHANES 数据集中成年人身高的平均标准误差的示例。直方图显示了 bootstrap 样本中平均值的分布，而红线显示了基于样本平均值和标准差的正态分布。

图 8.4 显示，通过自助法样本的均值分布与基于正态分布假设的理论估计相当接近。通常情况下，我们不会使用自助法来计算均值的置信区间（因为我们通常可以假设正态分布适用于均值的抽样分布，只要我们的样本足够大），但这个例子展示了这种方法给我们带来了与基于正态分布的标准方法大致相同的结果。自助法更常用于生成我们知道或怀疑正态分布不适用的其他统计量的标准误差。此外，在后面的章节中，您将看到我们还可以使用自助法样本来生成我们样本统计量的不确定性估计。

8.6 学习目标

阅读完本章后，您应该能够：

• 描述蒙特卡洛模拟的概念。

• 描述统计学中随机性的含义

• 描述伪随机数是如何生成的

• 描述自助法的概念

8.7 建议阅读

• 计算机时代的统计推断：算法、证据和数据科学，作者：布拉德利·埃夫隆（Bradley Efron）和特雷弗·哈斯蒂（Trevor Hastie）

第九章：假设检验

原文：statsthinking21.github.io/statsthinking21-core-site/hypothesis-testing.html

译者：飞龙

协议：CC BY-NC-SA 4.0

在第一章中，我们讨论了统计学的三个主要目标：

• 描述

• 决定

• 预测

在本章中，我们将介绍使用统计数据做出决策的思想，特别是关于某个特定假设是否得到数据支持的决策。

9.1 零假设统计检验（NHST）

我们将讨论的特定类型的假设检验被称为零假设统计检验（NHST）（出于将要明确的原因）。如果你拿起几乎任何科学或生物医学研究出版物，你会看到 NHST 被用来测试假设，在他们的心理学入门教科书中，Gerrig & Zimbardo（2002）将 NHST 称为“心理研究的支柱”。因此，学习如何使用和解释假设检验的结果对于理解许多研究领域的结果至关重要。

然而，你也需要知道，NHST 存在严重缺陷，许多统计学家和研究人员（包括我自己）认为它已经导致了科学上的严重问题，我们将在第[18]章（进行可重复研究.html#进行可重复研究）中讨论。50 多年来，人们一直呼吁放弃 NHST，转而采用其他方法（就像我们将在接下来的章节中讨论的那些方法）：

• “心理研究中的统计显著性检验可以被视为研究进行中一种基本的无意识”（Bakan，1966）

• 假设检验是“关于构成科学进步的错误观点”（Luce，1988）

NHST 也被广泛误解，主要是因为它违反了我们对统计假设检验应该如何工作的直觉。让我们看一个例子来看看这一点。

9.2 零假设统计检验：一个例子

人们对警察佩戴身体摄像头的兴趣很大，认为这可以减少使用武力并改善警察的行为。然而，为了证实这一点，我们需要实验证据，政府越来越普遍地使用随机对照试验来测试这样的想法。华盛顿特区政府和华盛顿特区警察局在 2015/2016 年进行了一项关于身体摄像头有效性的随机对照试验。警察被随机分配佩戴或不佩戴身体摄像头，然后跟踪他们的行为，以确定摄像头是否导致使用武力减少以及有关警察行为的民事投诉减少。

在我们得出结果之前，让我们问一下你认为统计分析可能是如何工作的。假设我们想具体测试佩戴摄像头是否减少使用武力的假设。随机对照试验为我们提供了测试假设的数据，即分配给摄像头组或对照组的警官使用武力的比率。下一个明显的步骤是查看数据，并确定它们是否提供有力的证据支持或反对这一假设。也就是说：鉴于数据和我们所知道的其他一切，佩戴身体摄像头是否减少了使用武力的可能性有多大？

事实证明，这不是零假设检验的工作方式。相反，我们首先拿出我们感兴趣的假设（即佩戴身体摄像头会减少使用武力），然后将其颠倒过来，创建一个零假设 - 在这种情况下，零假设将是摄像头不会减少使用武力。重要的是，我们假设零假设为真。然后我们看数据，并确定如果零假设为真，数据会有多大可能性。如果数据在零假设下不够可能，我们可以拒绝零假设，支持备择假设，这是我们感兴趣的假设。如果没有足够的证据来拒绝零假设，那么我们说我们保留（或“未能拒绝”）零假设，坚持我们最初的假设零假设为真。

理解 NHST 的一些概念，特别是臭名昭著的“p 值”，第一次遇到它们无疑是具有挑战性的，因为它们是如此违反直觉。正如我们将在后面看到的，还有其他方法可以提供更直观的方式来处理假设检验（但它们也有自己的复杂性）。然而，在我们接触这些方法之前，你有必要深刻理解假设检验的工作原理，因为显然它不会很快消失。

9.3 零假设检验的过程

我们可以将零假设检验的过程分解为几个步骤：

1. 制定一个包含我们预测的假设（在看到数据之前）

2. 指定零假设和备择假设

3. 收集与假设相关的一些数据

4. 将模型拟合到代表备择假设的数据中，并计算一个检验统计量

5. 计算假设为真时观察值的概率

6. 评估结果的“统计显著性”

举个实际例子，让我们使用 NHANES 数据来问以下问题：体力活动是否与身体质量指数有关？在 NHANES 数据集中，参与者被问及是否经常参与中等或剧烈强度的体育、健身或娱乐活动（存储在变量$PhysActive$中）。研究人员还测量了身高和体重，并用它们来计算身体质量指数（BMI）：

$$BMI=\frac{weight(kg)}{height(m{)}^2}$$

9.3.1 步骤 1：制定感兴趣的假设

我们假设不参与体力活动的人的 BMI 比参与的人更高。

9.3.2 步骤 2：指定零假设和备择假设

对于步骤 2，我们需要指定我们的零假设（我们称之为$H_0$）和我们的备择假设（我们称之为$H_A$）。$H_0$是我们测试感兴趣的假设的基准：也就是说，如果没有效应，我们期望数据看起来会是什么样子？零假设总是涉及某种形式的相等（=，$\le$或$\ge$）。$H_A$描述了如果实际上有效应，我们期望的情况。备择假设总是涉及某种形式的不等式（$\ne$，>或<）。重要的是，零假设检验在假设零假设为真的情况下进行。

我们还必须决定是否要测试定向或非定向假设。非定向假设只是预测会有差异，而不预测差异的方向。对于 BMI/活动的例子，非定向零假设将是：

$H0:BM{I}_{active}=BM{I}_{inactive}$

相应的非定向备择假设将是：

$HA:BM{I}_{active}\ne BM{I}_{inactive}$

另一方面，定向假设预测了差异的方向。例如，我们有强烈的先验知识来预测参与体力活动的人应该比不参与的人体重更轻，因此我们提出以下定向零假设：

$H0:BM{I}_{active}\ge BM{I}_{inactive}$

和定向备择假设：

$HA:BM{I}_{active}<BM{I}_{inactive}$

正如我们将在后面看到的，测试非定向假设更为保守，因此通常更可取，除非有强有力的先验理由假设特定方向上的效应。假设，包括它们是否是定向的，应该在查看数据之前始终明确指定！

9.3.3 步骤 3：收集一些数据

在这种情况下，我们将从 NHANES 数据集中抽取 250 个个体。图 9.1 展示了这样一个样本的示例，其中 BMI 分别显示为活跃和不活跃的个体，表 9.1 显示了每组的摘要统计信息。

表 9.1：活动与不活动个体的 BMI 数据总结

身体活动	N	均值	标准差
编号	131	30	9.0
是	119	27	5.2

图 9.1：来自 NHANES 数据集成年人样本的 BMI 数据的箱线图，按是否报告参与定期体育活动进行分割。

9.3.4 步骤 4：对数据进行建模并计算检验统计量

接下来，我们希望使用数据计算一个统计量，最终让我们决定是否拒绝零假设。为此，模型需要量化支持备择假设的证据量，相对于数据的变异性。因此，我们可以将检验统计量视为提供效应大小相对于数据变异性的一种度量。一般来说，这个检验统计量将与概率分布相关联，因为这使我们能够确定在零假设下我们观察到的统计量的概率有多大。

对于 BMI 的例子，我们需要一个检验统计量，允许我们测试两个均值之间的差异，因为假设是以每组的平均 BMI 来陈述的。经常用于比较两个均值的统计量是t统计量，最初由统计学家威廉·西利·高斯特(Wiliam Sealy Gossett)开发，他在都柏林的吉尼斯啤酒厂工作，并以笔名“学生”写作，因此通常被称为“学生t统计量”。当样本量相对较小且总体标准差未知时，t统计量适用于比较两组的均值。用于比较两个独立组的t统计量计算如下：

$$t=\frac{\overline{X_1}-\overline{X_2}}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}}$$

其中${\bar{X}}_1$和${\bar{X}}_2$是两组的均值，$S_1^2$和$S_2^2$是两组的估计方差，$n_1$和$n_2$是两组的样本量。因为两个独立变量的差异的方差是每个单独变量的方差的总和($var(A-B)=var(A)+var(B)$)，我们将每组的方差除以它们的样本量，以计算差异的标准误差。因此，可以将t统计量视为量化组间差异与均值差异的抽样变异性之间的大小关系的一种方式。

t统计量根据一个被称为t分布的概率分布进行分布。t分布看起来非常类似于正态分布，但它根据自由度的数量而有所不同。当自由度很大（比如 1000），那么t分布看起来基本上就像正态分布，但当自由度很小时，t分布的尾部比正态分布要长（见图 9.2）。在最简单的情况下，如果组的大小相同且方差相等，t检验的自由度就是观察值的数量减去 2，因为我们计算了两个均值，因此放弃了两个自由度。在这种情况下，从箱线图中很明显可以看出，非活跃组的变异性比活跃组更大，并且每组的数字也不同，因此我们需要使用一个稍微复杂一点的自由度公式，通常被称为“韦尔奇 t 检验”。公式为：

$$d.f.=\frac{{\left(\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}\right)}^2}{\frac{{\left(S_1^2/n_1\right)}^2}{n_1-1}+\frac{{\left(S_2^2/n_2\right)}^2}{n_2-1}}$$

当方差和样本大小相等时，这将等于$n_1+n_2-2$，否则会更小，实际上对样本大小或方差的差异对检验施加了惩罚。对于这个例子，计算结果为 241.12，略低于从样本大小减去 2 得到的 248。

图 9.2：每个面板显示了 t 分布（蓝色虚线）叠加在正态分布（红色实线）上。左面板显示了自由度为 4 的 t 分布，此时分布类似但尾部略宽。右面板显示了自由度为 1000 的 t 分布，此时它几乎与正态分布相同。

9.3.5 第 5 步：确定零假设下观察结果的概率

这一步是 NHST 开始违反我们的直觉的地方。我们不是确定在数据给定的情况下零假设为真的可能性，而是确定在零假设下观察到至少与我们观察到的统计量一样极端的可能性 — 因为我们最初假设零假设为真！为了做到这一点，我们需要知道在零假设下统计量的预期概率分布，这样我们就可以问在该分布下结果有多大可能性。请注意，当我说“结果有多大可能性”时，我真正的意思是“观察到的结果或更极端的结果有多大可能性”。我们需要添加这个警告的原因至少有两个。第一个是当我们谈论连续值时，任何特定值的概率都是零（如果你上过微积分课程，可能还记得）。更重要的是，我们试图确定如果零假设成立，我们的结果有多奇怪，任何更极端的结果都会更奇怪，因此在计算零假设下我们的结果的概率时，我们希望计算所有这些更奇怪的可能性。

我们可以使用理论分布（如t分布）或使用随机化来获得这个“零分布”。在我们转向 BMI 的例子之前，让我们从一些更简单的例子开始。

9.3.5.1 P 值：一个非常简单的例子

假设我们想要确定一枚特定硬币是否有偏向翻转为正面的倾向。为了收集数据，我们翻转了 100 次硬币，假设我们数到了 70 次正面。在这个例子中，$H_0:P(正面)\le 0.5$ 和 $H_A:P(正面)>0.5$，我们的检验统计量就是我们数到的正面次数。然后我们想要问的问题是：如果正面的真实概率是 0.5，那么我们观察到 100 次翻转中 70 次或更多正面的可能性有多大？我们可以想象这可能偶尔会发生，但似乎不太可能。为了量化这个概率，我们可以使用二项分布：

$$P(X\le k)=\sum _{i=0}^k\left(\genfrac{}{}{0ex}{}{N}{k}\right)p^i(1-p{)}^{(n-i)}$$

这个方程将告诉我们在特定的头像概率（$p$）和事件数量（$N$）的情况下，特定数量的头像（$k$）或更少的概率。然而，我们真正想知道的是特定数量或更多的概率，我们可以通过减去一来获得，根据概率规则：

$$P(X\ge k)=1-P(X<k)$$

图 9.3：100,000 次模拟运行中头像数量（100 次翻转）的分布，观察到的 70 次翻转由垂直线表示。

使用二项分布，给定 P(头像)=0.5，69 个或更少头像的概率为 0.999961，因此 70 个或更多头像的概率就是 1 减去这个值（0.000039）。这个计算告诉我们，如果硬币确实是公平的，那么得到 70 个或更多头像的可能性是非常小的。

现在，如果我们没有一个标准函数告诉我们那个数量的头像的概率会怎么样？我们可以通过模拟来确定，我们重复翻转一枚硬币 100 次，使用真实概率 0.5，然后计算这些模拟运行中头像数量的分布。图 9.3 显示了这个模拟的结果。在这里我们可以看到，通过模拟计算的概率（0.000030）非常接近理论概率（0.000039）。

9.3.5.2 使用t分布计算 p 值

现在让我们使用t分布来计算我们 BMI 示例的 p 值。首先，我们使用上面计算的样本值计算t统计量，我们发现 t = 3.86。然后我们想要问的问题是：如果组之间的真实差异为零或更小（即方向性零假设），那么我们会发现这样大小的t统计量的可能性是多少？

我们可以使用t分布来确定这个概率。在上面我们注意到，适当的自由度（在校正方差和样本大小的差异后）是 t = 241.12。我们可以使用统计软件中的函数来确定找到大于或等于我们观察到的t统计值的概率。我们发现 p(t > 3.86, df = 241.12) = 0.000072，这告诉我们，如果零假设确实成立，那么我们观察到的t统计值 3.86 相对不太可能。

在这种情况下，我们使用了定向假设，因此我们只需要查看零分布的一端。如果我们想要测试非定向假设，那么我们需要能够确定效应大小的意外程度，而不考虑其方向。在 t 检验的背景下，这意味着我们需要知道统计量在正向或负向方向上有多么意外的可能性。为了做到这一点，我们将观察到的 t 值乘以 -1，因为 t 分布以零为中心，然后将两个尾部概率相加，得到 双尾 p 值：p(t > 3.86 或 t< -3.86, df = 241.12) = 0.000145。在这里，我们看到双尾检验的 p 值是单尾检验的两倍，这反映了一个极端值不那么令人惊讶，因为它可能发生在任何方向。

你如何选择使用单尾还是双尾检验？双尾检验总是更保守，所以最好使用双尾检验，除非你有非常强烈的先验理由使用单尾检验。在这种情况下，你应该在查看数据之前就写下假设。在第 18 章中，我们将讨论假设的预先注册的概念，这正式了在查看实际数据之前写下假设的想法。一旦查看了数据，你绝对不应该对如何进行假设检验做出决定，因为这可能会导致结果严重偏倚。

9.3.5.3 使用随机化计算 p 值

到目前为止，我们已经看到了如何使用 t 分布来计算零假设下数据的概率，但我们也可以使用模拟来做到这一点。基本思想是，我们生成类似于零假设下预期数据的模拟数据，然后询问观察到的数据与这些模拟数据相比有多极端。关键问题是：我们如何生成使零假设成立的数据？一般的答案是，我们可以以一种特定的方式随机重新排列数据，使数据看起来像如果零假设真的成立时会是什么样子。这类似于自举的概念，因为它使用我们自己的数据来得出答案，但它的方式不同。

9.3.5.4 随机化：一个简单的例子

让我们从一个简单的例子开始。假设我们想比较足球运动员和越野跑步者的平均深蹲能力，其中 $H_0:{\mu }_{FB}\le {\mu }_{XC}$ 和 $H_A:{\mu }_{FB}>{\mu }_{XC}$。我们测量了 5 名足球运动员和 5 名越野跑步者的最大深蹲能力（我们将随机生成），假设 ${\mu }_{FB}=300$，${\mu }_{XC}=140$，和 $\sigma =30$。数据如表 9.2 所示。

表 9.2：两组深蹲数据

组	深蹲	打乱的深蹲
FB	265	125
FB	310	230
FB	335	125
FB	230	315
FB	315	115
XC	155	335
XC	125	155
XC	125	125
XC	125	265
XC	115	310

图 9.4：左：模拟足球运动员和越野跑步者深蹲能力的箱线图。右：在混淆组标签后分配给每组受试者的箱线图。

从图 9.4 的左侧图表可以清楚地看出两组之间存在很大的差异。我们可以进行标准的 t 检验来测试我们的假设；在这个例子中，我们将使用 R 中的 t.test() 命令，得到以下结果：

## 
##  Welch Two Sample t-test
## 
## data:  squat by group
## t = 8, df = 5, p-value = 2e-04
## alternative hypothesis: true difference in means between group FB and group XC is greater than 0
## 95 percent confidence interval:
##  121 Inf
## sample estimates:
## mean in group FB mean in group XC 
##              291              129

如果我们看一下这里报告的 p 值，我们会发现在零假设下出现这样的差异的可能性非常小，使用t分布来定义零。

现在让我们看看如何使用随机化来回答相同的问题。基本思想是，如果没有组之间的差异的零假设成立，那么来自哪个组（足球运动员与越野跑步者）就不重要 - 因此，为了创建像我们实际数据一样但也符合零假设的数据，我们可以随机重新排列数据集中个体的数据，然后重新计算组之间的差异。这样的洗牌结果显示在表 9.2 的“shuffleSquat”列中，生成的数据的箱线图显示在图 9.4 的右面板中。

图 9.5：在随机洗牌组成员资格后，足球和越野组之间的平均差异的 t 值的直方图。垂直线表示两组之间观察到的实际差异，虚线显示了此分析的理论 t 分布。

在混淆数据之后，我们看到两组现在更加相似，事实上越野组现在的平均值略高。现在让我们这样做 10000 次，并存储每次迭代的t统计量；如果你在自己的电脑上进行这个操作，完成需要一段时间。图 9.5 显示了所有随机洗牌的t值的直方图。如预期的那样，在零假设下，这个分布以零为中心（分布的均值为 0.007）。从图中我们还可以看到，在洗牌后t值的分布大致遵循零假设下的理论t分布（均值=0），表明随机化工作生成了零数据。我们可以通过测量多少洗牌值至少与观察值一样极端来计算来自随机数据的 p 值：p(t > 8.01, df = 8) using randomization = 0.00410。这个 p 值与我们使用t分布得到的 p 值非常相似，两者都非常极端，表明如果零假设成立，观察到的数据非常不可能出现 - 在这种情况下，我们知道它不是真的，因为我们生成了数据。

9.3.5.4.1 随机化：BMI/活动示例

现在让我们使用随机化来计算 BMI/活动示例的 p 值。在这种情况下，我们将随机洗牌PhysActive变量，并在每次洗牌后计算两组之间的差异，然后将我们观察到的t统计量与洗牌数据的t统计量的分布进行比较。图 9.6 显示了来自洗牌样本的t值的分布，我们还可以计算找到一个与观察值一样大或更大的值的概率。从随机化得到的 p 值（0.000000）与使用t分布得到的 p 值（0.000075）非常相似。随机化检验的优势在于，它不要求我们假设每个组的数据都是正态分布的，尽管 t 检验通常对该假设的违反具有相当的鲁棒性。此外，随机化检验可以让我们计算统计量的 p 值，即使我们没有像 t 检验那样的理论分布。

图 9.6：在组标签混洗后 t 统计直方图，垂直线显示 t 统计的观察值，至少与观察值一样极端的值显示为浅灰色

当我们使用随机化检验时，我们必须做出一个主要假设，我们称之为可交换性。这意味着所有的观察结果都以相同的方式分布，这样我们可以互换它们而不改变整体分布。这种假设可能会破坏的主要地方是当数据中存在相关的观察结果时；例如，如果我们有来自 4 个不同家庭的个体数据，那么我们不能假设个体是可交换的，因为兄弟姐妹之间的距离比他们与其他家庭的个体之间的距离更近。一般来说，如果数据是通过随机抽样获得的，那么可交换性的假设应该成立。

9.3.6 步骤 6：评估结果的“统计显著性”

下一步是确定从前一步得出的 p 值是否足够小，以至于我们愿意拒绝零假设，相反地得出替代假设是真实的。我们需要多少证据？这是统计学中最具争议的问题之一，部分原因是因为它需要主观判断——没有“正确”的答案。

历史上，对这个问题最常见的答案是，如果 p 值小于 0.05，我们应该拒绝零假设。这来自于罗纳德·费舍尔的著作，他被称为“20 世纪统计学中最重要的人物”（Efron 1998）：

“如果 P 在 .1 和 .9 之间，肯定没有理由怀疑被检验的假设。如果它低于 .02，强烈表明假设未能解释所有的事实。如果它低于 .05，我们不会经常走错路……在大约我们可以说的水平上画一条线：要么治疗有效，要么发生了一次在二十次试验中不会再次发生的巧合”（R. A. Fisher 1925）

然而，费舍尔从未打算 $p<0.05$ 成为一个固定的规则：

“没有科学工作者有一个固定的显著性水平，从一年到另一年，在所有情况下，他拒绝假设；相反，他根据他的证据和想法来考虑每个特定情况”（罗纳德·艾尔默·费舍尔 1956）

相反，p < .05 很可能成为一种仪式，因为在计算变量的任意值的 p 值变得容易之前，人们依赖于使用表格的 p 值。所有的表格都有一个 0.05 的条目，这样就很容易确定自己的统计量是否超过了达到那个显著水平所需的值。

统计阈值的选择仍然存在深刻的争议，最近（Benjamin et al., 2018）提出将默认阈值从 0.05 更改为 0.005，使其更严格，因此更难拒绝零假设。在很大程度上，这一举措是由于越来越多的人担心从 $p<.05$ 的显著结果获得的证据相对较弱；我们将在第 18 章中讨论可重复性时返回到这一点。

9.3.6.1 假设检验作为决策：内曼-皮尔逊方法

而 Fisher 认为 p 值可以提供关于特定假设的证据，统计学家 Jerzy Neyman 和 Egon Pearson 则强烈反对。相反，他们提出我们应该从长期的错误率角度来考虑假设检验：

“基于概率理论的任何测试本身都不能提供任何有价值的关于假设真假的证据。但我们可以从另一个角度来看待测试的目的。在不希望知道每个单独假设是真还是假的情况下，我们可以寻找规则来指导我们对待它们的行为，通过遵循这些规则，我们确保在长期的经验中，我们不会经常犯错”（J. Neyman and Pearson 1933）

也就是说：我们无法知道具体的决策是对还是错，但如果我们遵循规则，至少可以知道我们的决策在长期内会有多少错误。

为了理解 Neyman 和 Pearson 开发的决策框架，我们首先需要讨论统计决策的结果类型。现实存在两种可能的状态（$H_0$为真，或$H_0$为假），以及两种可能的决策（拒绝$H_0$，或保留$H_0$）。我们可以做出正确决策的两种方式：

• 当$H_0$为假时我们拒绝$H_0$（在信号检测理论的术语中，我们称之为命中）

• 当$H_0$为真时我们保留$H_0$（在这种情况下有些令人困惑，这被称为正确拒绝）

我们也可以犯两种错误：

• 当$H_0$实际上为真时我们拒绝$H_0$（我们称之为虚警，或I 型错误）

• 当$H_0$实际上为假时我们保留$H_0$（我们称之为漏失，或II 型错误）

Neyman 和 Pearson 创造了两个术语来描述长期内这两种错误的概率：

• P(I 型错误) = $\alpha$

• P(II 型错误) = $\beta$

也就是说，如果我们将$\alpha$设为 0.05，那么长期内我们应该有 5%的概率犯 I 型错误。虽然通常将$\alpha$设为 0.05，但可接受的$\beta$水平的标准值为 0.2——也就是说，我们愿意接受 20%的时间我们无法检测到真实效应。我们将在后面讨论统计功效时再回到这一点，统计功效是 II 型错误的补充。

9.3.7 显著结果意味着什么？

关于 p 值的实际含义存在很多混淆（Gigerenzer, 2004）。假设我们进行一个实验，比较不同条件下的平均值，发现 p 值为 0.01。可能有多种解释。

9.3.7.1 这意味着零假设为真的概率是 0.01 吗？

不是。请记住，在零假设检验中，p 值是给定零假设下数据的概率（$P(data|H_0)$）。它并不支持关于给定数据的零假设的概率（$P(H_0|data)$）的结论。当我们在后面的章节讨论贝叶斯推断时，我们将回到这个问题，因为贝叶斯定理让我们以一种方式反转条件概率，从而能够确定给定数据的假设概率。

9.3.7.2 这意味着你做出错误决策的概率是 0.01 吗？

不是。这将是$P(H_0|data)$，但请记住，p 值是在$H_0$下数据的概率，而不是假设的概率。

9.3.7.3 这意味着如果你再次进行研究，你会 99%的时间得到相同的结果吗？

不是。p 值是关于在零假设下特定数据集的可能性的陈述；它不允许我们对未来事件的可能性（如重复实验）进行推断。

9.3.7.4 这意味着你发现了一个实际重要的效应吗？

不。统计显著性和实际显著性之间存在重要区别。举个例子，假设我们进行了一项随机对照试验，以检验某种特定饮食对体重的影响，并且我们发现在 p<.05 的水平上存在统计学上显著的影响。这并不能告诉我们实际上减掉了多少体重，这被称为效应大小（将在第 10 章中更详细地讨论）。如果我们考虑一项减肥研究，那么我们可能不认为失去一盎司（即几片薯条的重量）是实际上显著的。让我们看看随着样本量的增加，我们能否检测到 1 盎司的显著差异。

图 9.7 显示，随着样本量的增加，显著结果的比例增加，因此在非常大的样本量（约 262,000 名受试者）中，当两种饮食之间的体重减少差异为 1 盎司时，我们将在超过 90%的研究中发现显著结果。尽管这些是统计上显著的，但大多数医生不会认为减重一盎司在实际上或临床上是显著的。当我们回到第 10.3 节讨论统计功效的概念时，我们将更详细地探讨这种关系，但从这个例子中已经很清楚，统计显著性并不一定表明实际显著性。

图 9.7：对于一个非常小的变化（1 盎司，大约为.001 标准差）的显著结果的比例，作为样本量的函数。

9.4 现代语境下的 NHST：多重检验

到目前为止，我们已经讨论了我们感兴趣的测试单个统计假设的例子，这与传统科学一致，传统科学通常一次只测量少量变量。然而，在现代科学中，我们通常可以测量每个个体的数百万个变量。例如，在量化整个基因组的遗传研究中，每个个体可能有数百万个测量值，在我所在的大脑成像研究中，我们经常一次从大脑的 10 万多个位置收集数据。在这些情况下应用标准的假设检验，除非我们适当地加以注意，否则会发生不好的事情。

让我们举个例子来看看这可能是如何工作的。人们对了解可以使个体易患严重精神疾病（如精神分裂症）的遗传因素非常感兴趣，因为我们知道大约 80%的精神分裂症患者之间的差异是由遗传差异引起的。人类基因组计划及随后的基因组科学革命提供了工具，可以检查人类在基因组方面的许多差异。近年来使用的一种方法称为全基因组关联研究（GWAS），其中对每个个体的基因组进行表征，以确定他们在每个位置的遗传密码中有哪些字母，重点关注人类经常不同的位置。确定了这些位置后，研究人员在基因组的每个位置进行统计检验，以确定被诊断为精神分裂症的人是否更有可能在该位置具有遗传序列的一个特定版本。

让我们想象一下，如果研究人员简单地询问每个位置的测试是否在 p<.05 水平上显著，而实际上在任何位置都没有真正的效应会发生什么。为了做到这一点，我们从零分布中生成大量模拟的t值，并询问有多少个在 p<.05 水平上显著。让我们多次这样做，每次计算有多少测试结果显著（见图 9.8）。

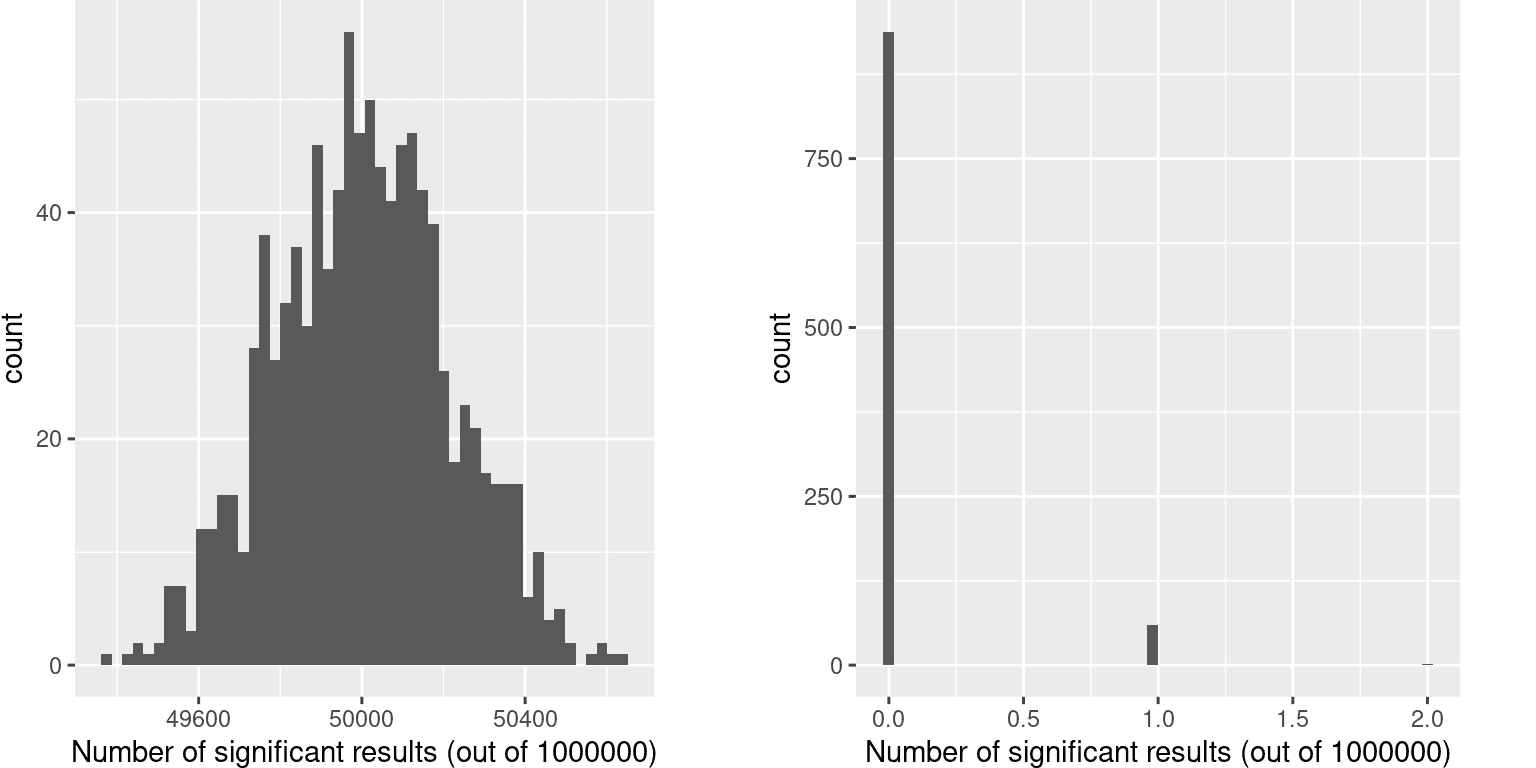
图 9.8：左：当实际上没有真正效应时，在每一百万次统计测试中每组显著结果的直方图。右：应用多重测试的邦费罗尼校正后，在所有模拟运行中显著结果的直方图。

这表明每次运行中约 5%的测试都是显著的，这意味着即使在真正没有显著关系的情况下，如果我们将 p < .05 作为统计显著性的阈值，那么即使在每项研究中也会“发现”约 500 个基因在统计上是显著的（显著结果的预期数量简单地是$n\ast \alpha$）。这是因为虽然我们控制了每次测试的错误，但我们没有控制整个测试家族的错误率（称为家族智误差），这才是我们真正想要控制的，如果我们要查看大量测试的结果。在上面的例子中，使用 p<.05，我们的家族智误差率是 1 - 也就是说，在任何特定研究中，我们几乎肯定会至少犯一个错误。

控制家族智误差的一种简单方法是将α水平除以测试次数；这被称为邦费罗尼校正，以意大利统计学家卡洛·邦费罗尼命名。使用上面例子中的数据，我们可以看到在图 9.8 中，只有约 5%的研究显示出任何显著结果，使用校正后的α水平 0.000005，而不是名义水平 0.05。我们有效地控制了家族智误差，使得我们研究中出现任何错误的概率控制在 0.05 左右。

9.5 学习目标

• 识别假设检验的组成部分，包括感兴趣的参数、零假设和备择假设以及检验统计量。

• 描述 p 值的正确解释以及常见的误解

• 在假设检验中区分两种类型的错误以及决定它们的因素。

• 描述如何使用重抽样来计算 p 值。

• 描述多重检验的问题以及如何解决

• 描述零假设统计检验的主要批评。

9.6 建议阅读

• 《无意义的统计学》，作者格尔德·吉格伦策

参考资料

Efron, Bradley. 1998. “R. A. Fisher in the 21st Century (Invited Paper Presented at the 1996 r. A. Fisher Lecture).” Statist. Sci. 13 (2): 95–122. https://doi.org/10.1214/ss/1028905930.
Fisher, R. A. 1925. Statistical Methods for Research Workers. Edinburgh Oliver & Boyd.
Fisher, Ronald Aylmer. 1956. Statistical Methods and Scientific Inference. New York: Hafner Pub. Co.
Neyman, J., and K. Pearson. 1933. “On the Problem of the Most Efficient Tests of Statistical Hypotheses.” Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 231 (694-706): 289–337. https://doi.org/10.1098/rsta.1933.0009.

这篇关于斯坦福 Stats60：21 世纪的统计学：第五章到第九章的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---