MATLAB - 四旋翼飞行器动力学方程

本文主要是介绍MATLAB - 四旋翼飞行器动力学方程，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

系列文章目录

前言

本例演示了如何使用 Symbolic Math Toolbox™（符号数学工具箱）推导四旋翼飞行器的连续时间非线性模型。具体来说，本例讨论了 getQuadrotorDynamicsAndJacobian 脚本，该脚本可生成四旋翼状态函数及其雅各布函数。这些函数将在使用非线性模型预测控制（模型预测控制工具箱）控制四旋翼飞行器的示例中使用。

四旋翼飞行器又称四旋翼直升机，是一种拥有四个旋翼的直升机。从四旋翼飞行器的质量中心出发，旋翼呈等距离的正方形排列。四旋翼的运动是通过调整四个旋翼的角速度来控制的，而四个旋翼是由电动马达带动旋转的。四旋翼飞行器动力学数学模型可从牛顿-欧拉方程和欧拉-拉格朗日方程中导出 [1]。

一、定义状态变量和参数

如图所示，四旋翼飞行器有六个自由度（三个线性坐标和三个角度坐标），四个控制输入。

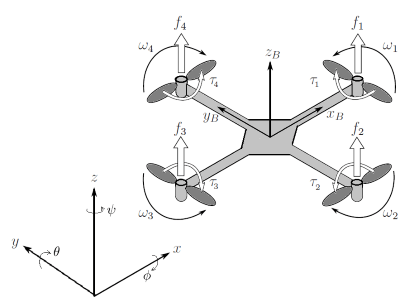
四旋翼飞行器的 12 个状态是

$\left(x,y,z,\phi\,,\theta,\psi,\dot{x},\dot{y},\dot{\ z},\dot{\phi},\dot{\theta},\dot{\psi}\right)^{T},$

其中

$\xi=(x,y,z)^{\mathrm{T}}$ 表示线性位置。

$\eta=\left(\phi\,,\theta,\psi\right)^{\mathrm{T}}$ 分别表示滚转角、俯仰角和偏航角。

$\left(\dot{x},\dot{y},\dot{z},\dot{\phi},\dot{\theta},\dot{\psi}\right)^{T}$ 表示线速度和角速度，或线性位置和角度位置的时间导数。

四旋翼飞行器的运动参数为

$(u_1,u_2,u_3,u_4)=\left(\omega_{1}^{2},\omega_{2}^{2},\omega_{3}^{2},\omega_{4}^{2}\right)$ 代表四个旋翼的角速度平方。

$(I_{{xx}},I_{{yy}},I_{{zz}})$ 代表机身坐标系中转动惯量矩阵的对角元素。

(k,l,m,b,g）代表升力常数、转子与质量中心的距离、四旋翼质量、阻力常数和重力。

前四个参数 $(u_1,u_2,u_3,u_4)$ 是控制输入或控制四旋翼飞行器轨迹的操纵变量。其余参数固定为给定值。

二、定义变换矩阵和科里奥利矩阵

定义惯性坐标系和主体坐标系之间的变换矩阵。需要这些变换矩阵来描述四旋翼飞行器在两个坐标系中的运动。四旋翼飞行器的 12 个状态在惯性系中定义，旋转惯性矩阵在机身系中定义。

创建符号函数来表示随时间变化的角度。在按照 [1] 进行的数学推导中，需要这种明确的时间依赖性来评估时间导数。定义矩阵 Wη 以将角速度从惯性系转换到体坐标系。定义旋转矩阵 R，使用局部函数部分定义的 rotationMatrixEulerZYX 函数将线性力从机身坐标系转换到惯性坐标系。创建符号矩阵来表示这些变换矩阵。

% Create symbolic functions for time-dependent angles
% phi: roll angle
% theta: pitch angle
% psi: yaw angle
syms phi(t) theta(t) psi(t)% Transformation matrix for angular velocities from inertial frame
% to body frame
W = [ 1,  0,        -sin(theta);0,  cos(phi),  cos(theta)*sin(phi);0, -sin(phi),  cos(theta)*cos(phi) ];% Rotation matrix R_ZYX from body frame to inertial frame
R = rotationMatrixEulerZYX(phi,theta,psi);

求用于表示惯性系中旋转能量的雅各布矩阵 $J=W_{\eta}^{T}\,I\,W_{\eta}$ 。

% Create symbolic variables for diagonal elements of inertia matrix
syms Ixx Iyy Izz% Jacobian that relates body frame to inertial frame velocities
I = [Ixx, 0, 0; 0, Iyy, 0; 0, 0, Izz];
J = W.'*I*W;

接下来，找出科里奥利矩阵 $C(\eta,\dot{\eta})=\frac{\mathrm{d}}{\mathrm{d}t}J-\frac{1}{2}\frac{\partial}{\partial\eta}\left(\dot{\eta}^{\Upsilon}J\right)$ ，它包含角欧拉-拉格朗日方程中的陀螺项和向心项。使用符号 diff 和 jacobian 函数进行微分运算。为了简化微分后科里奥利矩阵的符号，可以用 $C(\eta,{\dot{\eta}})$ 中的显式时间相关项替换为符号变量（代表特定时间的某些值）。这种简化的符号使这里的结果更容易与 [1] 中的推导进行比较。

% Coriolis matrix
dJ_dt = diff(J);
h_dot_J = [diff(phi,t), diff(theta,t), diff(psi,t)]*J;
grad_temp_h = transpose(jacobian(h_dot_J,[phi theta psi]));
C = dJ_dt - 1/2*grad_temp_h;
C = subsStateVars(C,t);

三、证明科里奥利矩阵定义是一致的

科里奥利矩阵 $C(\eta,{\dot{\eta}})$ 很容易用上一节的符号工作流程推导出来。然而，这里的 $C(\eta,{\dot{\eta}})$ 定义与 [1] 中的不同，后者使用克里斯托弗符号推导科里奥利矩阵。由于 $C(\eta,{\dot{\eta}})$ 并非唯一，因此可以有多种定义方法。但是，欧拉-拉格朗日方程中使用的 $C(\eta,\dot{\eta})\;\dot{\eta}$ 项必须是唯一的。本节将证明 $C(\eta,{\dot{\eta}})$ 的符号定义与 [1] 中的定义是一致的，即 $C(\eta,\dot{\eta})\;\dot{\eta}$ 项在两个定义中在数学上是相等的。

利用上一节中得出的 $C(\eta,{\dot{\eta}})$ 的符号定义来评估 $C(\eta,\dot{\eta})\;\dot{\eta}$ 项。

% Evaluate C times etadot using symbolic definition
phidot   = subsStateVars(diff(phi,t),t);
thetadot = subsStateVars(diff(theta,t),t);
psidot   = subsStateVars(diff(psi,t),t);
Csym_etadot = C*[phidot; thetadot; psidot];

使用 [1] 中得出的 $C(\eta,{\dot{\eta}})$ 的定义，对 $C(\eta,\dot{\eta})\;\dot{\eta}$ 项进行评估。

% Evaluate C times etadot using reference paper definition
C11 = 0;
C12 = (Iyy - Izz)*(thetadot*cos(phi)*sin(phi) + psidot*sin(phi)^2*cos(theta)) ...+ (Izz - Iyy)*(psidot*cos(phi)^2*cos(theta)) - Ixx*psidot*cos(theta);
C13 = (Izz - Iyy)*psidot*cos(phi)*sin(phi)*cos(theta)^2;
C21 = (Izz - Iyy)*(thetadot*cos(phi)*sin(phi) + psidot*sin(phi)^2*cos(theta)) ...+ (Iyy - Izz)*psidot*cos(phi)^2*cos(theta) + Ixx*psidot*cos(theta);
C22 = (Izz - Iyy)*phidot*cos(phi)*sin(phi);
C23 = - Ixx*psidot*sin(theta)*cos(theta) + Iyy*psidot*sin(phi)^2*sin(theta)*cos(theta) ...+ Izz*psidot*cos(phi)^2*sin(theta)*cos(theta);
C31 = (Iyy - Izz)*psidot*cos(theta)^2*sin(phi)*cos(phi) - Ixx*thetadot*cos(theta);
C32 = (Izz - Iyy)*(thetadot*cos(phi)*sin(phi)*sin(theta) + phidot*sin(phi)^2*cos(theta)) ...+ (Iyy - Izz)*phidot*cos(phi)^2*cos(theta) + Ixx*psidot*sin(theta)*cos(theta) ...- Iyy*psidot*sin(phi)^2*sin(theta)*cos(theta) - Izz*psidot*cos(phi)^2*sin(theta)*cos(theta);
C33 = (Iyy - Izz)*phidot*cos(phi)*sin(phi)*cos(theta)^2 ...- Iyy*thetadot*sin(phi)^2*cos(theta)*sin(theta) ...- Izz*thetadot*cos(phi)^2*cos(theta)*sin(theta) + Ixx*thetadot*cos(theta)*sin(theta);
Cpaper = [C11, C12, C13; C21, C22, C23; C31 C32 C33];
Cpaper_etadot = Cpaper*[phidot; thetadot; psidot];
Cpaper_etadot = subsStateVars(Cpaper_etadot,t);

证明这两个定义对 $C(\eta,\dot{\eta})\;\dot{\eta}$ 项给出了相同的结果。

tf_Cdefinition = isAlways(Cpaper_etadot == Csym_etadot)

tf_Cdefinition = 3x1 logical array111

四、查找运动方程

求出 12 个状态的运动方程。

根据 [1]，求出扭矩 τ B 在滚转、俯仰和偏航角方向上的扭矩：

通过降低第 2 个转子的速度和提高第 4 个转子的速度来设定滚转运动。
通过降低第 1 个转子的速度和提高第 3 个转子的速度来设置俯仰运动。
偏航运动是通过增大两个相对旋翼的速度和减小另外两个旋翼的速度来实现的。

求转子 T 在机身 Z 轴方向上的总推力。

% Define fixed parameters and control input
% k: lift constant
% l: distance between rotor and center of mass
% m: quadrotor mass
% b: drag constant
% g: gravity
% ui: squared angular velocity of rotor i as control input
syms k l m b g u1 u2 u3 u4% Torques in the direction of phi, theta, psi
tau_beta = [l*k*(-u2+u4); l*k*(-u1+u3); b*(-u1+u2-u3+u4)];% Total thrust
T = k*(u1+u2+u3+u4);

接下来，创建符号函数来表示随时间变化的位置。为线性位置、角度及其时间导数定义 12 个状态 $\left[\xi;\eta;\;{\dot{\xi}};\;{\dot{\eta}}\right]$ 。定义好状态后，用显式时间项代替，以简化符号。

% Create symbolic functions for time-dependent positions
syms x(t) y(t) z(t)% Create state variables consisting of positions, angles,
% and their derivatives
state = [x; y; z; phi; theta; psi; diff(x,t); diff(y,t); ...diff(z,t); diff(phi,t); diff(theta,t); diff(psi,t)];
state = subsStateVars(state,t);

建立描述 12 个状态 $f=\left[\,\dot{\xi};\,\dot{\eta}\,;\,\ddot{\xi}\,;\,\ddot{\eta}\,\right]$ 的时间导数的 12 个运动方程。线性加速度的微分方程为 $\ddot{\xi}\,=-(0,0,g)^{\Gamma}+R(0,0,T)^{\Gamma}/m.$ ，角加速度的微分方程为 $\ddot{\eta}=J^{-1}\bigl(\tau B-C(\eta,\dot{\eta})\,\dot{\eta}\,\bigr)\,.$ 。代入明确的时间相关项，以简化符号。

f = [ % Set time-derivative of the positions and anglesstate(7:12);% Equations for linear accelerations of the center of mass-g*[0;0;1] + R*[0;0;T]/m;% Euler–Lagrange equations for angular dynamicsinv(J)*(tau_beta - C*state(10:12))
];f = subsStateVars(f,t);

在前面的步骤中，固定参数被定义为符号变量，以紧跟文献 [1] 的推导。接下来，用给定值替换固定参数。这些值用于设计四旋翼飞行器特定配置的轨迹跟踪控制器。替换固定参数后，使用简化对运动方程进行代数简化。

% Replace fixed parameters with given values here
IxxVal = 1.2;
IyyVal = 1.2;
IzzVal = 2.3;
kVal = 1;
lVal = 0.25;
mVal = 2;
bVal = 0.2;
gVal = 9.81;f = subs(f, [Ixx Iyy Izz k l m b g], ...[IxxVal IyyVal IzzVal kVal lVal mVal bVal gVal]);
f = simplify(f);

五、为非线性模型预测控制查找雅各布因子并生成文件

最后，使用符号数学工具箱查找非线性模型函数的解析雅各布因子并生成 MATLAB® 文件。这一步骤对于提高使用模型预测控制工具箱™ 解决轨迹跟踪非线性模型时的计算效率非常重要。更多信息，请参阅 nlmpc（模型预测控制工具箱）和 Specify Prediction Model for Nonlinear MPC（模型预测控制工具箱）。

查找状态函数相对于状态变量和控制输入的雅各布。

% Calculate Jacobians for nonlinear prediction model
A = jacobian(f,state);
control = [u1; u2; u3; u4];
B = jacobian(f,control);

生成状态函数和状态函数 Jacobians 的 MATLAB 文件。这些文件可用于设计轨迹跟踪控制器，详见《使用非线性模型预测控制（模型预测控制工具箱）控制四旋翼飞行器》。

% Create QuadrotorStateFcn.m with current state and control
% vectors as inputs and the state time-derivative as outputs
matlabFunction(f,'File','QuadrotorStateFcn', ...'Vars',{state,control});% Create QuadrotorStateJacobianFcn.m with current state and control
% vectors as inputs and the Jacobians of the state time-derivative
% as outputs
matlabFunction(A,B,'File','QuadrotorStateJacobianFcn', ...'Vars',{state,control});

您可以在 getQuadrotorDynamicsAndJacobian.m 文件中访问该脚本中的代码。

六、函数

function [Rz,Ry,Rx] = rotationMatrixEulerZYX(phi,theta,psi)
% Euler ZYX angles conventionRx = [ 1,           0,          0;0,           cos(phi),  -sin(phi);0,           sin(phi),   cos(phi) ];Ry = [ cos(theta),  0,          sin(theta);0,           1,          0;-sin(theta),  0,          cos(theta) ];Rz = [cos(psi),    -sin(psi),   0;sin(psi),     cos(psi),   0;0,            0,          1 ];if nargout == 3% Return rotation matrix per axesreturn;end% Return rotation matrix from body frame to inertial frameRz = Rz*Ry*Rx;
endfunction stateExpr = subsStateVars(timeExpr,var)if nargin == 1 var = sym("t");endrepDiff = @(ex) subsStateVarsDiff(ex,var);stateExpr = mapSymType(timeExpr,"diff",repDiff);repFun = @(ex) subsStateVarsFun(ex,var);stateExpr = mapSymType(stateExpr,"symfunOf",var,repFun);stateExpr = formula(stateExpr);
endfunction newVar = subsStateVarsFun(funExpr,var)name = symFunType(funExpr);name = replace(name,"_Var","");stateVar = "_" + char(var);newVar = sym(name + stateVar);
endfunction newVar = subsStateVarsDiff(diffExpr,var)if nargin == 1 var = sym("t");endc = children(diffExpr);if ~isSymType(c{1},"symfunOf",var)% not f(t)newVar = diffExpr;return;endif ~any([c{2:end}] == var)% not derivative wrt t onlynewVar = diffExpr;return;endname = symFunType(c{1});name = replace(name,"_Var","");extension = "_" + join(repelem("d",numel(c)-1),"") + "ot";stateVar = "_" + char(var);newVar = sym(name + extension + stateVar);
end

七、参考资料

[1] Raffo, Guilherme V., Manuel G. Ortega, and Francisco R. Rubio. "An integral predictive/nonlinear ℋ∞ control structure for a quadrotor helicopter". Automatica 46, no. 1 (January 2010): 29–39. https://doi.org/10.1016/j.automatica.2009.10.018.

[2] Tzorakoleftherakis, Emmanouil, and Todd D. Murphey. "Iterative sequential action control for stable, model-based control of nonlinear systems." IEEE Transactions on Automatic Control 64, no. 8 (August 2019): 3170–83. https://doi.org/10.1109/TAC.2018.2885477.

[3] Luukkonen, Teppo. "Modelling and control of quadcopter". Independent research project in applied mathematics, Aalto University, 2011.

这篇关于MATLAB - 四旋翼飞行器动力学方程的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！