本文主要是介绍一阶低通滤波器,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一阶低通滤波器
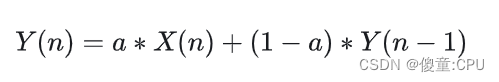
X为输入,Y为滤波后得到的输出值;本次的输出结果主要取决于上次的滤波输出值,其中a是和滤波效果有关的一个参数,称为滤波系数;它决定新采样值在本次滤波结果中所占的权重;

滤波系数a越小,滤波结果越平稳,但是灵敏度低;
滤波系数a越大,滤波结果越不稳定,但是灵敏度高;
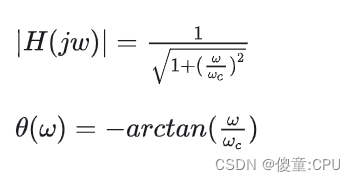
从幅值函数中可以看出:
当输入信号的频率小于截止频率时,幅值基本等于1,也就是输入信号能基本还原出有用信号的状态;
当输入信号的频率大于截止频率时,幅值就迅速小于1了,也就达到了衰减高频干扰信号的目的;
从相角函数中可以看出:
随着输入信号的频率的不断增大,输入信号的相位不断滞后,
当输入信号的频率等于截止频率时,相位滞后45度,
当输入信号的频率远大于截止频率时,相位滞后90度。
带宽截止频率的设计
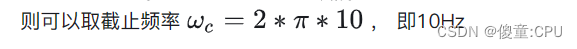
相移设计

采样周期的选取

例子

#include <stdio.h>
#include <stdlib.h>
#include <math.h>#define PI 3.14159265358979323846
//input 当前输入信号
//prev_output 上一个输出信号
//prev_input 上一个输入信号
//cutoff_freq 截止频率
//sample_rate 采样频率
double filter(double input, double prev_output, double prev_input, double cutoff_freq, double sample_rate) {double RC = 1.0 / (2.0 * PI * cutoff_freq);double alpha = 1.0 / (1.0 + RC * sample_rate);double output = alpha * (input + prev_input) + (1 - alpha) * prev_output;return output;
}int main() {double input_signal[] = {1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0};double output_signal[10];double prev_output = 0.0;double prev_input = 0.0;double cutoff_freq = 10.0; // 11Hzdouble sample_rate = 10000.0; // 10 kHzint i;for (i = 0; i < 10; i++) {output_signal[i] = filter(input_signal[i], prev_output, prev_input, cutoff_freq, sample_rate);prev_output = output_signal[i];prev_input = input_signal[i];}for (i = 0; i < 10; i++) {printf("%f\n", output_signal[i]);}return 0;
}
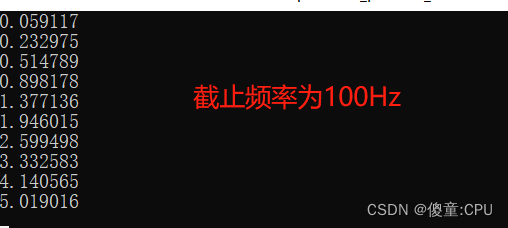


例子二
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define PI (3.141592f)typedef struct
{float ts; //采样周期(s)float fc; //截至频率(hz)float lastYn; //上一次滤波值float alpha; //滤波系数
} low_pass_filter_t;low_pass_filter_t low_pass_filter={0}; //定义滤波器//初始化滤波系数
void Init_lowPass_alpha(low_pass_filter_t* const filter,const float ts, const float fc)
{float b=2*M_PI*fc*ts;filter->ts=ts;filter->fc=fc;filter->lastYn=0;filter->alpha=b/(b+1);
}
//低通滤波 给你data 你处理了返回一个数据
float Low_pass_filter(low_pass_filter_t* const filter, const float data)
{float tem=filter->lastYn+(filter->alpha*(data-filter->lastYn));filter->lastYn=tem;return tem;}int main()
{Init_lowPass_alpha(&low_pass_filter,10000,10);float input[10] = {1,2,3,4,5,6,8,9,10};float output[10] = {0};for(int i = 0;i<10;i++){output[i] = Low_pass_filter(&low_pass_filter,input[i]);printf("%f\n",output[i]);}}
这篇关于一阶低通滤波器的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




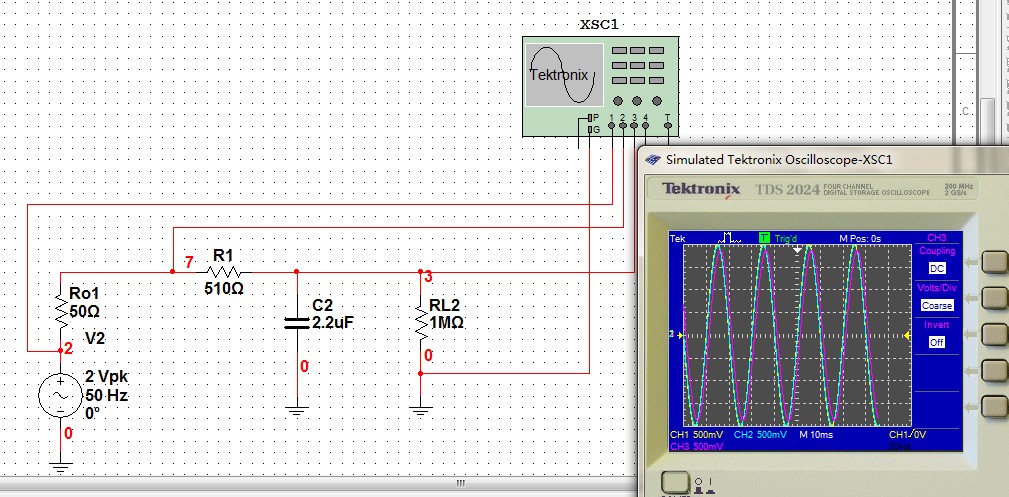

![[信号与系统]模拟域中的一阶低通滤波器和二阶滤波器](https://img-blog.csdnimg.cn/direct/8b2c16cd5f084d8a9a6eba3c68107ed8.png)
