本文主要是介绍基于SNN脉冲神经网络中的IF神经元matlab仿真,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、理论基础
二、核心程序
三、仿真结论
一、理论基础
SNN(Spiking Neural Network)脉冲神经网络是一种模拟神经系统中脉冲传递的神经网络模型。其中,IF(Integrate-and-Fire)神经元模型是一种常用的脉冲神经元模型。本文将详细介绍IF神经元脉冲在SNN中的具体实现步骤、数学公式以及其中的难点。 第三代神经网络,脉冲神经网络 (Spiking Neural Network,SNN) ,旨在弥合神经科学和机器学习之间的差距,使用最拟合生物神经元机制的模型来进行计算,更接近生物神经元机制。脉冲神经网络与目前流行的神经网络和机器学习方法有着根本上的不同。SNN 使用脉冲——这是一种发生在时间点上的离散事件——而非常见的连续值。每个峰值由代表生物过程的微分方程表示出来,其中最重要的是神经元的膜电位。本质上,一旦神经元达到了某一电位,脉冲就会出现,随后达到电位的神经元会被重置。对此,最常见的模型是 Leaky Integrate-And-Fire (LIF) 模型。此外,SNN 通常是稀疏连接的,并会利用特殊的网络拓扑。

同传统的人工神经网络一样,脉冲神经网络同样分为三种拓扑结构。它们分别是前馈型脉冲神经网络(feed-forward spiking neural network)、递归型脉冲神经网络(recurrent spiking neural network)和混合型脉冲神经网络(hybird spiking neural network)。
在脉冲神经网络(SNN)中,整流-火(Integrate-and-Fire,IF)神经元是一种简单但重要的模型,用于模拟神经元的电活动。IF神经元接收来自其他神经元的脉冲输入,根据输入的总量判断是否会发放输出脉冲。它是一种离散时间模型,通过积分输入来决定神经元是否激活。IF神经元的基本思想是在接收到一定数量的输入脉冲后,神经元会产生一个输出脉冲。通常,每个输入脉冲都会在神经元内部积分,累积成为一个内部电位。一旦内部电位达到阈值,神经元会发放一个输出脉冲,并且内部电位会被重置。
步骤一:电位积分 IF神经元模型通过积分输入电流来模拟神经元膜电位的变化。在每个时间步长上,神经元接收到来自其他神经元的输入电流,并将其累积到神经元的膜电位上。电位积分可以使用以下数学公式表示:
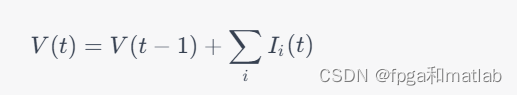
其中,V(t)表示时间$t$时刻的膜电位,V(t-1)表示上一个时间步长的膜电位,I_i(t)表示来自第i个神经元的输入电流。
实现难点:
- 输入电流的计算:膜电位的变化取决于来自其他神经元的输入电流。在实际应用中,如何准确计算输入电流是一个关键问题,涉及到神经元连接权重、突触传递机制等方面的处理。
- 时钟同步:为了模拟神经元的离散时间行为,SNN需要一个全局时钟来进行时间步长的同步。确保神经元在每个时间步长上同时更新是一个实现难点。
步骤二:脉冲发放 当膜电位超过一个阈值V_{\text{th}}时,IF神经元会发放一个脉冲,并将膜电位重置为一个初始值V_{\text{reset}}。脉冲发放过程可以使用以下数学公式表示:

其中,V_{\text{th}}表示阈值电位,V_{\text{reset}}表示脉冲发放后的重置电位。
实现难点:
- 阈值选择:选择合适的阈值V_{\text{th}}对于神经元的脉冲发放具有重要影响。过高或过低的阈值可能导致神经元无法正确发放脉冲或者频繁发放脉冲。
- 重置电位的确定:脉冲发放后,神经元需要将膜电位重置为一个初始值。确定合适的重置电位$V_{\text{reset}}$以确保膜电位的稳定性和正确的脉冲发放是一个挑战。
步骤三:膜电位衰减 为了模拟神经元膜电位的衰减,可以引入一个膜电位衰减因子\tau。膜电位在每个时间步长上都会根据该因子进行衰减。膜电位衰减过程可以使用以下数学公式表示:

其中,\tau表示膜电位衰减的时间常数。
实现难点:
- 衰减因子的选择:膜电位衰减因子$\tau$的选择对神经元膜电位的衰减速度有重要影响。合适的衰减因子需要根据实际应用中神经元的特性进行调整。
总结而言,IF神经元脉冲在SNN中的实现步骤包括电位积分、脉冲发放和膜电位衰减。通过积分输入电流、膜电位超过阈值发放脉冲以及膜电位的衰减,实现了脉冲神经元的模拟。实现IF神经元脉冲的难点包括输入电流的计算、时钟同步、阈值选择、重置电位的确定以及衰减因子的选择。克服这些难点可以实现高效而准确的SNN模型。
二、核心程序
.........................................................................AveRate_vect= zeros(0,length(I_vect_long));for I_In =I_vect_long; %loop over different I_In values I_Num = I_Num + 1; NumSpikes = 0; %holds number of spikes that have occurred i = 1; % index denoting which element of V is being assigned spike_flag=0;Times=t_ref/dt;%max timesV_vect(i)= V0; %first element of V, i.e. value of V at t=0 I_e_vect = I_In*ones(1,1+t_time/dt);for t=dt:dt:t_time %loop through values of t in steps of dt ms %INTEGRATE THE EQUATION tau*dV/dt = -V + IRRI =I_e_vect(i)*R_m;if (V_vect(i) > V_th) %cell spiked spike_flag=1;Times=0;NumSpikes = NumSpikes + 1; %add 1 to the total spike count end if (spike_flag==1)V_vect(i+1) = V_res; %set voltage back to V_resTimes=Times+1;else V_vect(i+1) = RI*dt/tau + (1-dt/tau)*V_vect(i); end if (Times==(t_ref/dt+1))spike_flag=0;endi = i + 1; %add 1 to index, corresponding to moving forward 1 time step end AveRate_vect(I_Num) =NumSpikes/t_time; %gives average firing rate in [#/sec = Hz] end
end
up2162三、仿真结论
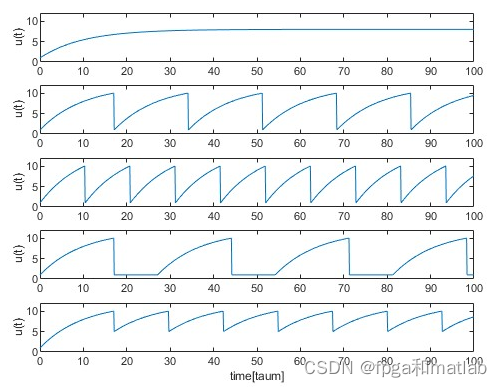
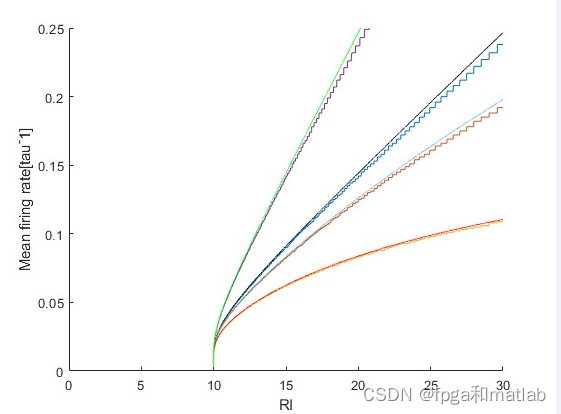
这篇关于基于SNN脉冲神经网络中的IF神经元matlab仿真的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




![C# double[] 和Matlab数组MWArray[]转换](/front/images/it_default2.jpg)



