《深度学习：Java语言实现》一一2.5神经网络的理论和算法

2.5神经网络的理论和算法
前面一节，你已经了解了使用机器学习进行数据分析的一般流程。这一节，我们会介绍神经网络的理论及算法（神经网络是机器学习众多方法之一），为接下来的深度学习内容做铺垫。
虽然我们只是轻描淡写地说 “神经网络”，它们的历史其实极其悠久。首个公开的神经网络算法名为“感知器（Perceptron）”，这篇名为“The perceptron: A perceiving and Recognizing Automaton (Project Para)”的论文由弗兰克·罗森布拉特（Frank Rosenblatt）发表于1957年。自那以后，人们研究、开发、发布了很多相关的方法，现在神经网络已经成为深度学习的基础元素之一。虽然我们简单地以“神经网络”一言以代之，实际上神经网络存在多种类型，我们会依照顺序介绍其中代表性的方法。
2.5.1单层感知器
感知器算法是神经网络算法中结构最简单的模型，它可以对两种类型进行线性分类。我们可以把它看成神经网络的原型。它是以最简单的方式模拟人类神经元的算法。
下图展示了通用模型的示意图：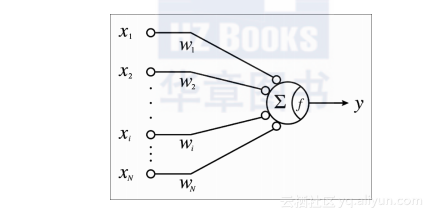

这幅图中的xi表示输入信号，Wi表示每一种输入信号对应的权重，y表示输出信号。f是激活函数。实际上，∑表示的是对所有输入数据的求和计算。请牢记，xi是依据预先定义的特征工程以非线性转换，所以xi是工程化的特征。
这样一来，感知器的输出可以表示如下：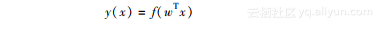

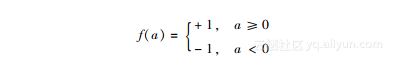
f(*)被称之为阶跃函数。正如上述公式中所展示的，感知器返回的输出是每个特征乘以其对应权重，然后求和，再将所求和作为阶跃函数的激活输入。其输出结果就是感知器的判断结果。训练过程中，你需要比较计算结果和正确的数据，并反馈错误的情况。
如果用t表示标识数据的值，那么上述公式可以改写为如下的形式：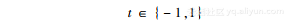

当标识数据属于类别1，即C1时，我们可以得到t=1。如果数据属于类别2，即C2时，t=-1。与此同时，如果输入数据可以进行正确的分类，我们可以如下结论：

将这些等式整合到一起，我们就能得到下面的公式，对每个恰当分类的数据，它都符合下面的等式：

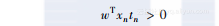
因此，通过最小化下面的函数，你可以增大感知器的准确度：

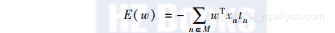
这里的E被称作“误差函数”。M表示错误分类的集合。为了最小误差函数，人们引入了梯度下降，也叫最速下降法，它是一种使用梯度递减方式寻找局部最小值的优化算法。该公式如下所示：

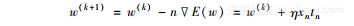
这里的η是学习速率，它是一个调整学习速率的通用算法优化参数，k表示算法中的步骤数。一般而言，学习速率（或简称“学习率”）越小，算法越容易取得局部最小值，因为这时模型无法覆盖旧的值。如果学习率很大，这种情况下，模型的参数无法收敛，因为计算的结果波动太大。因此，在实际操作中，学习率在最开始时被设置成一个比较大的值，随着每个迭代，不断地变小。另一方面，使用感知器时，如果数据是可以线性划分，算法的收敛就与学习率没有太大关系了，因此，这种情况下学习率被设置为1。
现在，我们一起来学习它的一个实现。实现中包的结构如下：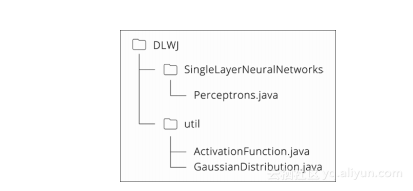

我们看看上幅图中Perceptronsjava的内容。主要的函数我们会逐一进行介绍。
首先，我们定义了学习需要的参数和常量。在前文介绍过，学习率（这段代码中，通过learningRate进行定义）可以是1：

毫无疑问，机器学习及深度学习都需要数据集进行学习和分类。本节中，想关注与感知器理论密切相关的实现。源代码中附有一份样本数据集，用于模型的训练和测试，示例代码中定义了名为GaussianDistribution的类，它按照正态分布（也叫高斯分布）返回某个值。我们在这里并不会一行行地详细解释源码，可以查看GaussianDistributionjava了解更多的内容。我们通过设置nln=2设置了学习数据的维度，它定义了下面这两种类型的实例：

使用g1random()（均值-20，方差10）以及g2random()（均值20，方差10）可以得到一组正态分布的数值。
使用这些值，通过［g1random()、g2random()］在类1中可以生成500个数据属性；同样，使用［g2random()、g1random()］生成另外500个数据属性。另外，请注意类1中的所有数据都标记为1，类2中的每个数据都标记为-1。最终的结果是类1中的所有数据都分布在［-20, 20］之间，而类2中的所有数据都分布在［20, -20］之间，因此，这些数据可以按照线性划分，不过其中的某些数据对接近的其他类而言就变成了噪声。
自此，我们已经准备好了数据，现在可以着手构建模型。输入层中的单元数“nln”在这里是一个输入参数，它决定了模型的轮廓（Outline）:

下面我们看一个实际的感知器构造器。这个感知器模型中只有网络的权重w，非常简单，如下所示：

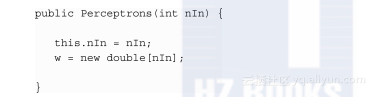
接下来就是最后一步训练。这种学习迭代会一直持续下去，直到学习集达到预设的数值，或者可以正确分类所有训练数据：

你可以按照我们之前介绍的途径，在train方法中使用梯度下降算法。这里的网络参数w已经更新了：

一旦你对足够的数据完成了学习并构建好模型，下一步就可以进行测试了。首先，我们可以使用训练好的模型检查测试数据的分类属于哪一类。

predict只是简单地通过网络激活了输入。这里的阶跃函数定义在ActivationFunction java中：

接下来，我们需要使用测试数据评判该模型的预测效果。这部分内容比较复杂，可能需要更进一步解释才可以理解。
通常而言，机器学习方法效果的判断指标是基于混淆矩阵的准确率（Accuracy）、精确度（Precision）以及召回率（Recall）。混淆矩阵对矩阵中预测正确的类和预测错误的类进行了归纳汇总，见下表所示：

这三个指标之间的关系如下：

准确率表示所有数据中正确分类的数据所占比率，精确度表示的是预测为正例的所有数据中实际为正例的数据所占的比率，召回率是预测为正例的数据占实际正例数据的比率。下面是实现这一功能的代码：

当你编译并运行Perceptronjava，可以得到990%的准确率、980%的精确率以及100%的召回率。这意味着所有实际正例的数据都得到了正确的划分，不过，还是有少部分实际负例的数据被错误地划分为了正例。在这段源代码中，因为这个数据集主要的目的是为了演示，所以这段代码中也没有包括K折交叉验证。上面示例中的数据集是通过程序生成，几乎没有什么干扰数据（Noise Data）。因此，它的准确率、精确率和召回率都很高，因为数据能够很好地进行分类。然而，正如前面曾经提到的，要仔细地研究预测的结果，尤其是在得到非常理想结果的时候。
2.5.2逻辑回归
看到逻辑回归这个名字，你大概就能猜测出逻辑回归是一种“回归模型”。不过，当看到它的公式时，你会发现逻辑回归使用线性区分模型泛化感知器。
逻辑回归可以被看成一种神经网络。在感知器中，我们使用阶跃函数作为激活函数，不过在逻辑回归中，我们使用（逻辑上的）sigmoid函数。sigmoid函数的数学定义如下所示：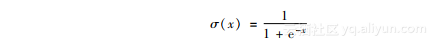

这一函数的图形解读如下：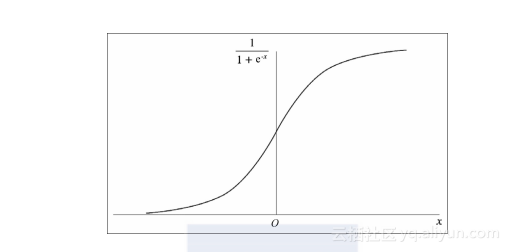

sigmoid函数可以将任意的实数映射为0到1之间的某个值。因此，逻辑回归的输出可以作为任何一个分类的后验概率。其对应的公式可以表示如下：

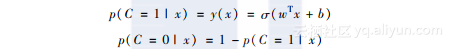
这两个公式可以整合在一起，如下所示：

这里正确的数t∈{0,1} 。你可能也注意到，它与我们在感知器中使用的数据区间略有不同。
基于前面的公式，用于评估模型参数的最大似然值的似然函数可以用下面的公式表示：

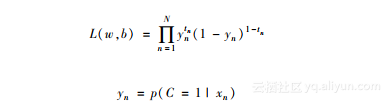
如你所见，这个公式中，需要进行优化的参数不仅是网络权重，还包括偏差b。
现在需要做的是最大化似然函数，不过这种计算量让人担忧，因为函数存在乘法计算。为了简化计算，我们对似然函数取对数。除此之外，我们对符号进行了替换，目的是最小化似然函数的负对数结果。由于对数函数是单调递增的，所以原函数的关系不会发生变化。该公式可以表示如下：

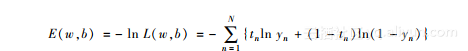
你能同时看到误差函数（Error Function）。这种类型的函数称为交叉熵误差函数（CrossEntropy Error Function）。
与感知器类似，可以通过计算模型参数w和b的梯度对模型进行优化。梯度可以通过如下公式描述：

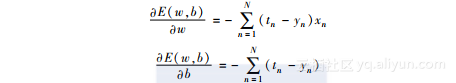
依据这些公式，我们可以更新模型参数，如下所示：

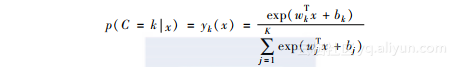
理论上说可以直接使用上述公式，并对其进行实现。不过，如你所料，这样一来要计算所有数据的总和，才能得出每次迭代的梯度。一旦数据集变大，计算的开销将会迅速增加。
因此，通常会采用另一种方式来进行，即从数据集中选择部分数据，仅对这些选中的数据求和来计算梯度，从而更新模型的参数。这种方法称为“随机梯度下降法”（Stochastic Gradient Descent, SGD），因为数据是从数据集中随机选择的。每次参数刷新所使用子集被称为“小批量（MiniBatch）”。
使用“小批量”的SGD有些时候也被称之为“小批量随机梯度下降（MiniBatch Stochastic Gradient Descent, MSGD）”。为了与之进行区别，随机地从数据集中选取某个数据进行学习的在线训练被称之为“随机梯度下降，SGD”。然而，本书中，我们把MSGD和SGD都统称为SGD，因为当分批处理的尺度为1时，它们二者并没有什么区别。由于对每个数据都进行学习会增加计算量，一种推荐的方式是使用“小批量处理”的方式。

就逻辑回归的实现而言，由于下一节介绍多类逻辑回归时会涉及，所以本节就不再提供代码示例了。
2.5.3多类逻辑回归
逻辑回归也可以应用于多类划分。二类划分中，激活函数是sigmoid函数，其输出值介于0和1之间，你可以凭借输出值对数据进行分类。那么，如果类别有K类，我们如何划分数据呢？幸运的是，这并不困难。我们可以使用softmax函数，将公式的输出改成K类成员概率向量，从而对多类数据进行划分。而softmax函数是sigmoid函数的多变量版本。每一类数据的后验概率可以表示如下：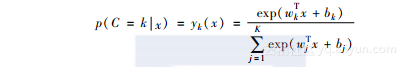

通过这一函数，你可以像二类划分那样，得到对应的似然函数以及负对数似然函数，如下所示：

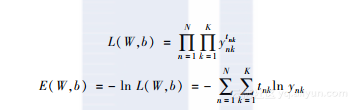
这里的W=［w1,…,wj,…,wk］, ynk=yk(xn)。同时，tnk是正确数据向量的第K个元素，tn它对应于第n个训练数据。如果输入数据属于类别K，那么tnk的值就为1，否则其值就为0。
损失函数关于权重向量和偏差等模型参数的梯度可以描述如下：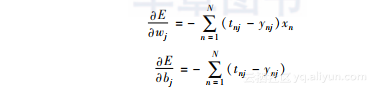

为了更好地理解这一理论，让我们一起看看它对应的源码。这其中，你可以看到与“小批量（MiniBatch）”相关变量以及模型需要的变量：

下面这段代码演示了训练数据洗牌打乱的过程，通过这种方式每个小批量都能随机地应用SGD算法：

由于我们已经了解了“多类划分（MultiClass Classification）”的问题，接下来，我们将生成三个类的样本数据集用了三个类。除了在感知器中使用的均值和方差，我们还引入了第三类数据集，它的训练数据和测试数据遵循正态分布，均值为00，方差为10。换句话说，每一类数据都遵循正态分布，均值为［-20, 20］，［20, -10］，以及［00, 00］，方差为1。我们将训练数据定义为int类型，被打过标签的测试数据定义为Integer类型。这样设计的目的是为了在评价模型时，处理测试数据更容易。此外，每一个标记数据都定义为一个数组，因为遵循“多类划分”原则，它的长度要与类别数量相匹配：

接下来，我们就可以使用之前定义的MiniBatchIndex将训练数据划分为一个个“小批量”：

自此，我们已经准备好了数据，让我们开始实际地构建一个模型：

逻辑回归模型的参数是网络权重W,以及偏差b：

处理完所有的 “小批量”训练才算结束。如果你将minibatchSize设置为1，即 minibatchSize=1，训练就转化为所谓的“在线训练（Online Training）”：

这段代码中，学习速率逐渐变小，使得模型得以收敛。现在，对于实际干活儿的训练方法train，你可以像下面这样将其划分为两个部分：
1使用“小批量”的数据计算W的梯度以及偏差b。
2用计算出来的梯度更新W和b：

在train方法末尾，返回了dY，它表示预测数据和正确数据的误差值。对于逻辑回归而言，这并非强制的，不过在机器学习和深度学习算法中，这是必需的，我们后面会介绍其中的缘由。
训练的下一步是就是测试了。逻辑回归中的测试过程与感知器中的测试过程相比，并没有什么实质的变化。
首先，在predict方法中，我们使用训练模型预测输入数据：

上述代码中调用的predict方法和output方法的定义如下：

首先，用output方法激活输入数据。参考上面的代码，你会看到在output方法的最后，激活函数使用了softmax函数。softmax方法定义在ActivateFunctionjava中，该方法返回一个数组，该数组显示了当前样本属于每个类别的概率，因此，你只需要找出数组中具有最高概率值的元素索引。该索引就代表了预测的类。
最后，我们还需要对模型进行评估。混淆矩阵再一次被应用于模型评估，不过我们需要特别小心，因为这一次，我们有多个类的分类，你需要找出每一个类的精确度或者召回率：

2.5.4多层感知器
单层神经网络存在着巨大的问题。感知器或者逻辑回归对于能够进行线性划分的问题而言还算比较高效，不过它们完全无法处理非线性的问题。譬如，它们甚至无法解决如下图所示最简单的异或（XOR）问题：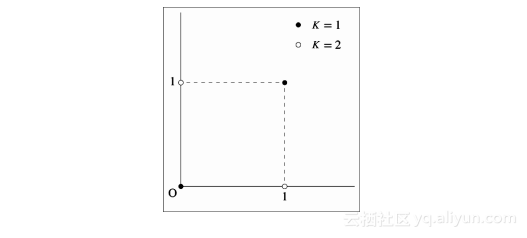

由于大多数现实世界的问题都是非线性的，感知器和逻辑回归都不能应用于这些场景。因此，算法又做了进一步的改良，来应对这些非线性的问题。这些就是多层感知器（MLP),或者称之为多层神经网络(MultiLayer Neural Networks）。从这个名字你大概也能猜出其中的变化，通过在输入层和输出层之间添加名为“隐藏层”的新的一层，网络具备了表示多种模式的能力。下图是多层神经网络的图像模式：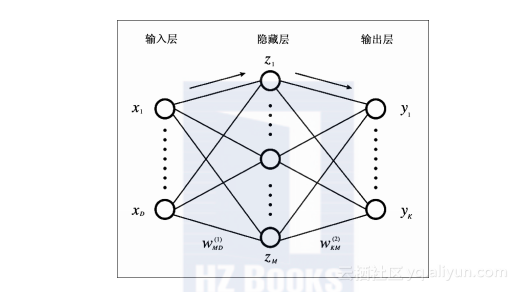

这幅图的目的并不是介绍跨层的连接。研究神经网络，无论是理论还是实现，我们都应尽量保证模型中有前向反馈的网络结构。遵循这些原则，同时增加“隐藏层”的数目，你往往能用不太复杂的数学模型逼近任意函数。
现在，让我们看看如何计算输出。乍一看，这似乎很复杂，不过它要做的事情和之前一样，还是累计各层以及网络的权重或激励，因此，你要做的就是简单地将各层的公式整合到一起。每个输出用公式可以表示如下：

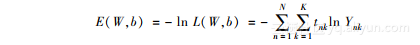
这个公式中，h是隐藏层的激活函数，g是输出层。
前面已经介绍过，对于多类划分（MutiClass Classfication）的情况，输出层的激活函数使用softmax方法计算非常高效，它对应的误差函数（Error Function）可以表示如下：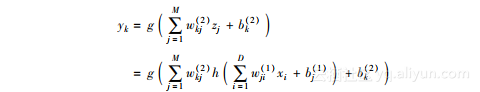

对单层网络而言，直接在输入层反映出这种误差没有太大的问题，然而，对多层网络来说，神经网络无法以一个整体的方式进行学习，除非这些错误同时出现在隐藏层和输入层。
幸运的是，前向反馈网络中有一种反向传播（Backpropagation）算法，它能通过前后向追踪网络，让误差可以高效地在模型中传播。我们一起看看这个算法的机制。为了增加算法的可读性，我们假设误差函数的计算发生于在线学习时，如下所示：

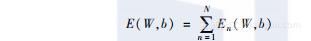
我们现在只考虑公式中的梯度En。由于大多数情况下，实际应用时数据集中的数据都相互独立，并且同分布的，因此像刚才那样进行定义完全没有问题。
前向反馈网络中的每个神经元可以看成连接到这个神经元的所有网络其权重的求和，因此，通用的表达式如下所示：

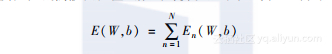
请注意，这里的xi不仅仅表示输入层的值（当然，它可以是输入层的值）。此外，h是非线性激活函数。权重的梯度和偏差的梯度可以表示如下：

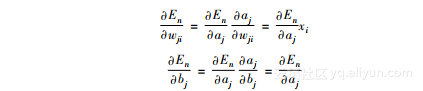
现在，我们用下面这个公式定义一个符号：

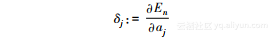
然后，我们就得到：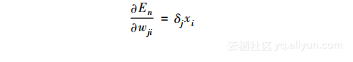

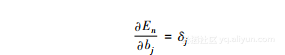
因此，我们比较这两个公式，输出神经元可以描述如下：

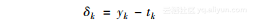
此外，隐藏层的每个单元可以表示为：

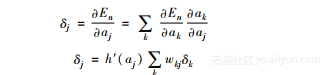
至此，我们完成了反向传播公式的介绍。因此，增量被称作反向传播的误差（Backpropagated Error）。通过计算反向传播的错误，我们可以得出权重和偏差。看着公式，你可能会觉得这比较困难，不过它所做的基本上就是从连接的单元接收误差的反馈并更新权重这一件事，因此也并没有那么困难。
现在，让我们用一个简单的异或问题做例子，看看如何实现。当你读完源码之后，会有更加清晰的理解。代码的包结构如下所示：

该算法的基本流程定义在MultiLayerPerceptronsjava中，不过反向传播的实际实现是在HiddenLayerjava中。我们使用多类逻辑回归实现输出层。由于我们并没有对LogisticRegressionjava进行任何修改，所以这部分代码本节就不再重复列出。我们在ActivationFunctionjava中新增了sigmoid函数和双曲正切函数（Hyperbolic Tangent）的求导。双曲正切函数常常作为sigmoid函数的可选替代，也是一种激活函数。此外，RandomGeneratorjava中，增加了基于均匀分布生成随机数的方法。这个函数会以随机方式初始化隐藏层的权重，这一步非常重要，因为模型经常因为这些初始值的设定问题陷入局部最优，无法完成对数据的分类。
我们看看MultiLayerPerceptronsjava的内容。MultiLayerPerceptronjava中为每一层分别定义了不同的类：HiddenLayer类用于隐藏层，LogisticRegression类用于输出层。这些类的实例分别定义为hiddenLayer以及logisticLayer：

MLP的参数是隐藏层HiddenLayer以及输出层LogisticRegression的权重W和偏差b。由于输出层和之前介绍的版本没有什么变化，所以我们这里不再复述它的代码了。HiddenLayer的构造器定义如下：

随机初始化w，其数目与神经元数目一致。实际上，这种初始化需要高度技巧，因为一旦初始值的分布不合适，你常常会面临局部最小的问题。因此，实际应用中，常常用一些随机种子对模型进行测试。激活函数既可以使用sigmoid函数，也可以使用双曲正切函数。
MLP的训练可以通过神经网络依次由前向传播和后向传播轮流进行：

从hiddenLayerbackward我们可以了解如何由逻辑回归，得到隐藏层的后向传播预测误差dY。请注意，反向传播也需要逻辑回归的输入值：

你大概会想这个算法太复杂了，很难懂，因为它的参数似乎很复杂，不过我们这里所做的几乎与我们在逻辑回归Train方法中所做的一样：我们使用”小批量”为单位计算了W和b的梯度，并更新了模型参数。就这么简单。那么，MLP可以解决异或问题了么？执行下MultiLayerPerceptronsjava看看它的结果吧。
结果只输出了模型准确率、精确率以及召回率的百分比，然而，举例而言，如果你使用LogisticRegression的predict方法查看预测数据的话，你会看到它实际的预测概率是多少，如下所示：