基于sigma-delta和MASHIII调制器的频率合成器simulink建模与仿真

本文主要是介绍基于sigma-delta和MASHIII调制器的频率合成器simulink建模与仿真，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.算法运行效果图预览

2.算法运行软件版本

3.部分核心程序

4.算法理论概述

4.1 Sigma-Delta调制器原理

4.2 数学模型

4.3 噪声整形

4.4 MASH III调制器原理

4.5 基于Sigma-Delta和MASH III的频率合成器

5.算法完整程序工程

1.算法运行效果图预览

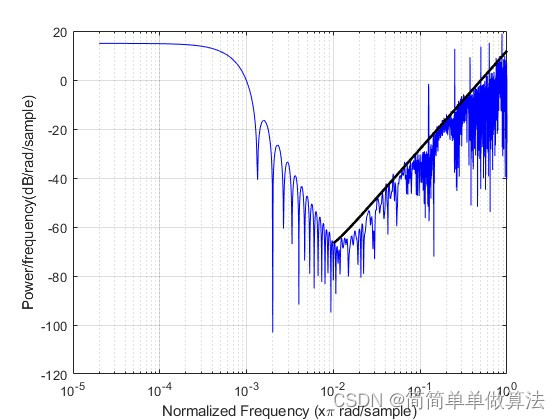
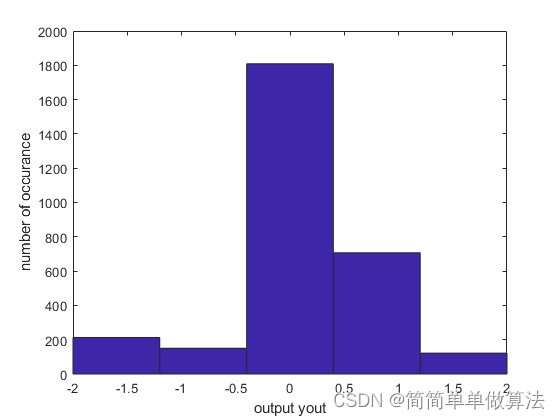
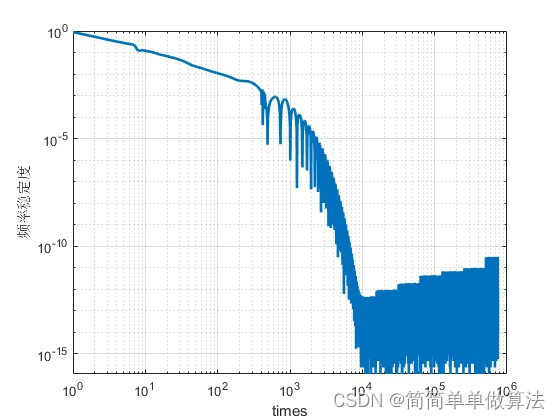
其误差当系统进入稳定状态的时候，频率误差就小于1E-9，并且随着频率的增加，其稳定性将更好。

2.算法运行软件版本

matlab2022a

3.部分核心程序

...........................................................................
window  = hann(length(yout));
[Pyy,w] = periodogram(yout,window,100000);
PSD2    = 1/M+1/100*(2*(w)).^4;
Len     = length(PSD2);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure;
semilogx(w/pi,10*log10(pi*Pyy),'b');
hold
semilogx(w(Len/100:Len)/pi,10*log10(PSD2(Len/100:Len)),'k','linewidth',2);
grid on
xlabel('Normalized Frequency (x\pi rad/sample)')
ylabel('Power/frequency(dB/rad/sample)');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
figure;
plot(yout,'linewidth',2);
grid on;
xlabel('times');
ylabel('sigmadelta调制器输出');
grid onfigure;
hist(yout,5)
xlabel('output yout')
ylabel('number of occurance');figure;
plot(yout2(1:3*Len/4),'linewidth',2);
grid on;
xlabel('times');
ylabel('V');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%分析频率稳定度
Fre = yout3;
K   = 1;
t1  = yout3(1:end-K);
t2  = yout3(K+1:end);Err = abs(t1-t2)./t1;
ttt = Err(20:end);
idx = find(ttt==0);
ttt(idx)=[];figure;
loglog(ttt,'linewidth',2);
grid on;
xlabel('times');
ylabel('频率稳定度');
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%最后进行杂散分析
N        = 16;             %累加器的位数；
K        = fix((2^N)*0.2); %频率控制字，即累加的步长；
D        = 8;             %8bit DAC
g        = gcd(K,2^N);
pe       = 2^N/(g);
n        = 1:pe;
pp       = pe+1;          %频谱分析点数
add_y    = mod(n*K,2^N);  %累加器的输出表达式；%设定量化区间
pat             = -1 + 1/ (2^ (D - 1) ):1/ (2^ (D - 1) ):1 - 1/ (2^ (D -1) ); 
%设定量化码本值
codebook        = -1 + 1/ (2^D):1/ (2^(D - 1) ) :1 - 1/ (2^D); 
rom_x           = cos(2*pi*add_y/(2^N));
[index,quants2] = quantiz(rom_x,pat,codebook);
[Pzz,wz]        = periodogram(quants2,[],'onesided',pp);figure; 
psdplot(Pzz/max(Pzz),wz);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
37_001m

4.算法理论概述

频率合成器是现代无线通信系统中的关键组件，用于生成精确且可调的频率信号。基于Sigma-Delta（Σ-Δ）调制器和MASH III（Multi-stage noise shaping and High-order single-loop）调制器的频率合成器结合了两种技术的优势，提供了高分辨率和低噪声的性能。

4.1 Sigma-Delta调制器原理

Sigma-Delta调制器（Σ-Δ ADC）以其高分辨率和内在的噪声整形特性而著称。在频率合成器中，Σ-Δ调制器用于将低频的模拟信号或相位误差转换为高速的单比特数据流。

Σ-Δ调制器通常由一个差分器、一个积分器（或多个积分器）、一个量化器和一个反馈DAC（数模转换器）组成。

Σ-Delta调制器的工作原理基于过采样和噪声整形。输入信号与反馈信号之差被积分，然后量化。量化产生的误差被反馈回输入端，形成闭环系统。

4.2 数学模型

Σ-Delta调制器的数学模型可以用以下差分方程表示：

Y[n] = X[n] + (1 - Z^-1) * E[n]

其中，Y[n]是输出信号，X[n]是输入信号，E[n]是量化误差，Z^-1表示单位延迟。

4.3 噪声整形

噪声整形是Σ-Δ调制器的关键特性，它将量化噪声推向高频，从而在低频范围内实现高信噪比（SNR）。

4.4 MASH III调制器原理

MASH III调制器是一种多级噪声整形和高阶单环结构，结合了多级Σ-Δ调制器的优点。MASH III调制器由多个级联的Σ-Δ调制器组成，每一级都有自己的量化器和反馈DAC。每一级的输出都被下一级用作输入的一部分，从而形成级联结构。最后一级的输出经过一个数字误差校正滤波器（DECF），以消除前面各级产生的量化噪声。MASH III调制器的数学模型相对复杂，涉及到多级Σ-Δ调制器的联合分析和数字滤波器的设计。

通过精心设计的噪声整形和误差消除机制，MASH III调制器能够在保持高分辨率的同时，显著降低带内噪声。