大学物理-实验篇——用拉伸法测定金属丝的杨氏(弹性)模量（胡克定律、杨氏模量、平面反射镜、三角函数、螺旋测微器）

2024-01-08 16:28
文章标签 实验 螺旋 弹性 平面 拉伸 大学物理 三角函数 杨氏 模量 杨氏模量 反射镜 金属丝 测微器 胡克定律 法测定

本文主要是介绍大学物理-实验篇——用拉伸法测定金属丝的杨氏(弹性)模量（胡克定律、杨氏模量、平面反射镜、三角函数、螺旋测微器），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

预备知识

力学：胡克定律（Hooke's law）

材料力学：杨氏模量

光学：平面反射镜

 数学：三角函数

螺旋测微器

实验目的 

实验仪器

实验原理 

1.拉伸法测杨氏弹性模量

2.光杠杆放大法测量微小伸长量

3.杨氏模量

实验步骤

1.测量金属丝直径d

2.调整支架位置，调节底座水平

3.放置光杠杆镜架，调节镜面竖直

4.调整镜尺组，直到清晰看到标尺

5.增减砝码，记录望远镜内刻度读数

6.测量刻度尺到反射镜间距D

7.测量光杠杆转动半径 l

8.测量金属丝的长度L

预备知识

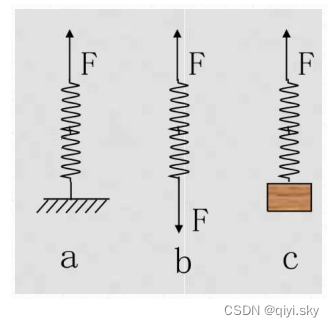
第一个预备知识是中学就学习过的胡克定律，简单看一下公式

力学：胡克定律（Hooke's law）

\Delta F=k\Delta x

  • 弹性限度内
  • 抵抗力
  • 形变方向相反

材料力学：杨氏模量

第二个是材料力学的：杨氏模量Young's modulus（1807) （拉伸模量）

  • 描述固体材料抵抗形变能力的物理量
  • 外力作用下材料产生弹性形变/塑性形变
  • 弹性形变下应变（形变）程度与外力成正比
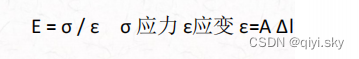
  • 以单位面积上承受的力表示，单位为N/m^2
  • 杨氏模量的大小标志了材料的刚性
  • 测量：动态法/静态法

光学：平面反射镜

  • 直线传播
  • 反射角=入射角
  • 光路可逆
  • 镜面转动角度vs出射光线转动角度

 数学：三角函数

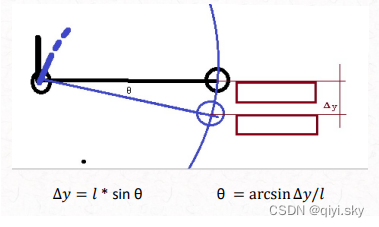
螺旋测微器

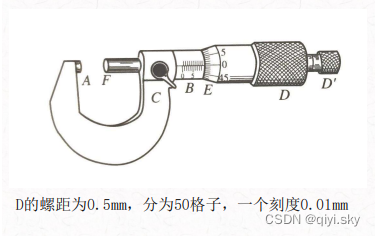
螺旋测微器的测砧A和固定刻度B固定在尺架C上；

可动刻度 E、旋钮微调旋钮D'是与测微螺杆 F 连在一起的，通过精密螺纹套在B上。

  1. 解除锁定
  2. 使用前，判断零误差
  3. 转动开口，略大于待测物
  4. 慢速转动D'，直到听到"喀喀"的声音
  5. 锁定读数，杆上和螺旋读数
  6. 解锁松开，取下待测物
  7. 锁定 收回盒中

螺旋测微器的读数方法： 

1.读出固定套筒上露出的刻线尺寸，一定要注意不能遗漏应读出的0.5mm刻线值。

2、读出微分筒上的尺寸，要看清微分筒圆周上哪一格与固定套筒的中线基准对齐，将格数乘0.01mm既得微分筒上的尺寸。

3、将上面的两个读数相加，即为螺旋测微器（千分尺）上测得尺寸。 

实验目的 

  1. 学习用拉伸法测杨氏模量的方法；
  2. 学习光杠杆放大法测微小长度变化的原理和方法；
  3. 掌握千分尺、望远镜的使用方法；
  4. 学习用逐差法处理数据；
  5. 学习正确选择测量仪器，从而体会误差理论对实验的指导意义。

实验仪器

  1. 杨氏模量测定仪
  2. 光杠杆
  3. 砝码
  4. 望远镜尺组
  5. 螺旋测微器
  6. 卷尺

实验原理 

1.拉伸法测杨氏弹性模量

给物体施以力的作用，物体将发生形变，在弹性限度范围内应变与应力的大小成正比，其比例系数的倒数即为杨氏模量，又称弹性模量。

以长度为L、横截面积为S的金属丝为例，在外力F的作用下，金属丝伸长量为\Delta L，在弹性限度范围内，则有

  • E：金属丝的杨氏模量
  • 单位：为N\cdot m^{-2}
  • 仅与材料的性质有关

2.光杠杆放大法测量微小伸长量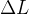\Delta L

光杠杆放大法是一种利用光学原理把微小长度的变化加以放大后，再进行测量的方法。

光杠杆放大法利用光杠杆放大装置将微小长度的变化放大为望远镜中标尺读数的变化。光杠杆放大装置包括光杠杆和镜尺组。

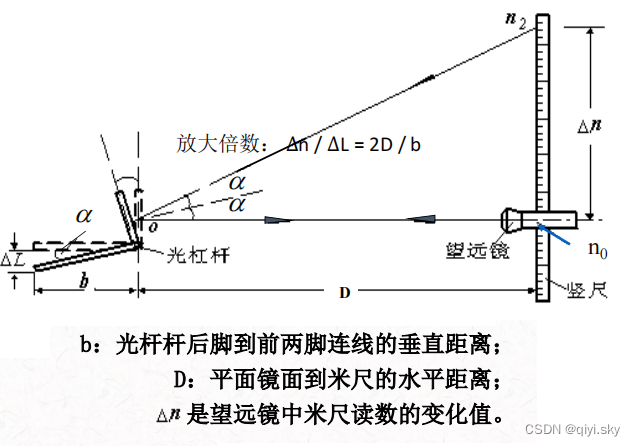
3.杨氏模量

将金属丝截面积S=\frac{\pi}{4}d^2代入，即可得到待测金属丝的杨氏模量公式为：

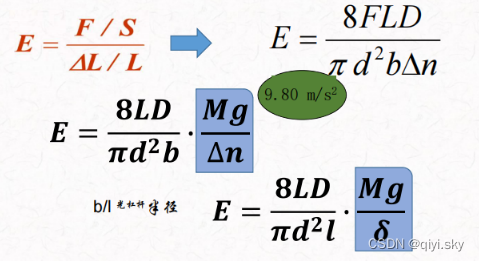
杨氏模量E的金属丝，观测到的位置变化\Delta n满足：

E=\frac{8LD}{\pi d^2b}\cdot \frac{Mg}{\Delta n} 

\Delta n(M)=\frac{8g}{\pi}\cdot \frac{D}{d^2b}\cdot \frac{L}{E}M

实验步骤

1.测量金属丝直径d

上中下的位置测量各两个数据，读数格式：0.###mm

d上中下平均
Mm121212

2.调整支架位置，调节底座水平

  1. 尽量远离实验台
  2. (杆平面)正对实验台
  3. 调平水平仪：气泡偏移的方向较高

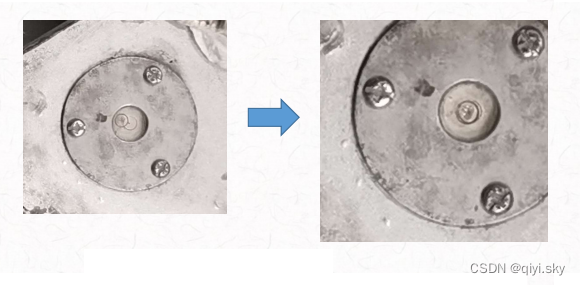
3.放置光杠杆镜架，调节镜面竖直

  1. F2、F3卡槽
  2. 拉长尾杆，F1托台
  3. 镜前旋钮调反射镜竖直

4.调整镜尺组，直到清晰看到标尺

镜架位置及高度

  • 正对支架，在中垂线上
  • 望远镜下缘与支架中平台平齐

开灯(红色激光）

  • 对准镜面，反射点落于尺上等高
  • 光点在支架轴对侧
  • 转镜筒调光点左右
  • 微调平面镜调光点高度

开灯(无激光）

  • 找绿光：微调望远镜方向
  • 找刻度：调节焦距

调刻度尺高度

  • 对0点：接近最佳
  • 调刻度尺高度：确保7砝码的最大偏转刻度可读取

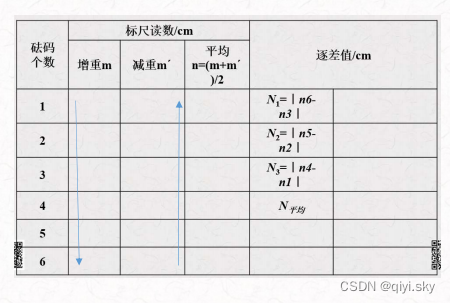
5.增减砝码，记录望远镜内刻度读数

砝码数: 0-1-2-3-4-5-6-7-6-5-4-3-2-1-0

注意：

  • 勿碰触支架和镜架
  • 砝码错位对放
  • 砝码盘稳定后读数
  • 砝码的质量精度    读数：± ##.# mm

M=1.000±0.001(Kg)

6.测量刻度尺到反射镜间距D

  1. 移除砝码后测量
  2. 镜面到镜架轴
  3. 卷尺水平拉直

读数： ####.# mm

D左上右平均
Mm

7.测量光杠杆转动半径 l

  1. 整体轻拿光杠杆
  2. 纸面拓印三点标记
  3. 规作图量垂距 l （计算F1到F2、F3连线的垂距）

读数： ##.# mm

l左上右平均
Mm

8.测量金属丝的长度L

  1. 上下夹线柱平面间距
  2. 拉直后测量(误差)
  3. 卷尺使用（卷尺抵紧一侧台面，卷尺拉直后读差值）

读数：####.# mm

L左上右平均
Mm

END

这篇关于大学物理-实验篇——用拉伸法测定金属丝的杨氏(弹性)模量（胡克定律、杨氏模量、平面反射镜、三角函数、螺旋测微器）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/584073。

相关文章

STM32(十一)：ADC数模转换器实验

STM32(十一)：ADC数模转换器实验

AD单通道： 1.RCC开启GPIO和ADC时钟。配置ADCCLK分频器。 2.配置GPIO，把GPIO配置成模拟输入的模式。 3.配置多路开关，把左面通道接入到右面规则组列表里。 4.配置ADC转换器， 包括AD转换器和AD数据寄存器。单次转换，连续转换；扫描、非扫描；有几个通道，触发源是什么，数据对齐是左对齐还是右对齐。 5.ADC_CMD 开启ADC。 void RCC_AD
阅读更多...
HNU-2023电路与电子学-实验3

HNU-2023电路与电子学-实验3

写在前面： 一、实验目的 1.了解简易模型机的内部结构和工作原理。 2.分析模型机的功能，设计 8 重 3-1 多路复用器。 3.分析模型机的功能，设计 8 重 2-1 多路复用器。 4.分析模型机的工作原理，设计模型机控制信号产生逻辑。 二、实验内容 1.用 VERILOG 语言设计模型机的 8 重 3-1 多路复用器； 2.用 VERILOG 语言设计模型机的 8 重 2-1 多
阅读更多...
【CSS in Depth 2 精译_024】4.2 弹性子元素的大小

【CSS in Depth 2 精译_024】4.2 弹性子元素的大小

当前内容所在位置（可进入专栏查看其他译好的章节内容） 第一章 层叠、优先级与继承（已完结） 1.1 层叠1.2 继承1.3 特殊值1.4 简写属性1.5 CSS 渐进式增强技术1.6 本章小结 第二章 相对单位（已完结） 2.1 相对单位的威力2.2 em 与 rem2.3 告别像素思维2.4 视口的相对单位2.5 无单位的数值与行高2.6 自定义属性2.7 本章小结 第三章 文档流与盒模型（已
阅读更多...
求空间直线与平面的交点

求空间直线与平面的交点

若直线不与平面平行，将存在交点。如下图所示，已知直线L过点m（m1，m2，m3），且方向向量为VL（v1，v2，v3），平面P过点n（n1，n2，n3），且法线方向向量为VP（vp1，vp2，vp3），求得直线与平面的交点O的坐标（x，y，z）： 将直线方程写成参数方程形式，即有： x = m1+ v1 * t y = m2+ v2 * t
阅读更多...
高斯平面直角坐标讲解，以及地理坐标转换高斯平面直角坐标

高斯平面直角坐标讲解，以及地理坐标转换高斯平面直角坐标

高斯平面直角坐标系（Gauss-Krüger 坐标系）是基于 高斯-克吕格投影 的一种常见的平面坐标系统，主要用于地理信息系统 (GIS)、测绘和工程等领域。该坐标系将地球表面的经纬度（地理坐标）通过一种投影方式转换为平面直角坐标，以便在二维平面中进行距离、面积和角度的计算。 一 投影原理 高斯平面直角坐标系使用的是 高斯-克吕格投影（Gauss-Krüger Projection），这是 横
阅读更多...
61.以太网数据回环实验（4）以太网数据收发器发送模块

61.以太网数据回环实验（4）以太网数据收发器发送模块

（1）状态转移图： （2）IP数据包格式： （3）UDP数据包格式： （4）以太网发送模块代码： module udp_tx(input wire gmii_txc ,input wire reset_n ,input wire tx_start_en , //以太网开始发送信
阅读更多...
LTspice模拟CCM和DCM模式的BUCK电路实验及参数计算

LTspice模拟CCM和DCM模式的BUCK电路实验及参数计算

关于BUCK电路的原理可以参考硬件工程师炼成之路写的《 手撕Buck！Buck公式推导过程》.实验内容是将12V~5V的Buck电路仿真,要求纹波电压小于15mv. CCM和DCM的区别: CCM:在一个开关周期内，电感电流从不会到0. DCM:在开关周期内，电感电流总会到0. CCM模式Buck电路仿真: 在用LTspice模拟CCM电路时,MOS管驱动信号频率为100Khz,负载为10R（可自
阅读更多...
HCIA--实验十：路由的递归特性

HCIA--实验十：路由的递归特性

递归路由的理解 一、实验内容 1.需求/要求： 使用4台路由器，在AR1和AR4上分别配置一个LOOPBACK接口，根据路由的递归特性，写一系列的静态路由实现让1.1.1.1和4.4.4.4的双向通信。 二、实验过程 1.拓扑图： 2.步骤： （下列命令行可以直接复制在ensp） 1.如拓扑图所示，配置各路由器的基本信息： 各接口的ip地址及子网掩码，给AR1和AR4分别配置
阅读更多...
算法练习题17——leetcode54螺旋矩阵

算法练习题17——leetcode54螺旋矩阵

题目描述 给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。  代码 import java.util.*;class Solution {public List<Integer> spiralOrder(int[][] matrix) {// 用于存储螺旋顺序遍历的结果List<Integer> result = new ArrayList
阅读更多...
n条直线最多能划分出多少个平面?

n条直线最多能划分出多少个平面?

N条直线，两两相交，其交点各不不同，则产生的交点数目为N个数中取2个数的组合； 同时，也只有这种情况下（两两相交，也交点不同），分割的平面数最多， 数目为： 2 + (N-1)(N+2)/2.  这里求最少平面数没有意义，因为最少平面数就是N+1, 即N条直线两两平行的时候，分割的平面最少。 举例： 1条直线分割平面数最多为2； a1 = 2 2条直线分割平面数最多为4；
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2