本文主要是介绍对极大极小搜索和阿尔法贝塔剪枝搜索算法的简单描述与理解--萌新向通俗易懂,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这是本人第一次正经写博客,排版技术不行,看起来可能有点难受,但我相信如果大家认真按顺序读下去一定能理解这个算法,如果还有不是很清楚或者觉得我哪里有讲错的地方欢迎评论留言!这段时间都在!会看和回复的!
阿尔法贝塔剪枝是基于极大极小值搜索的一种算法。
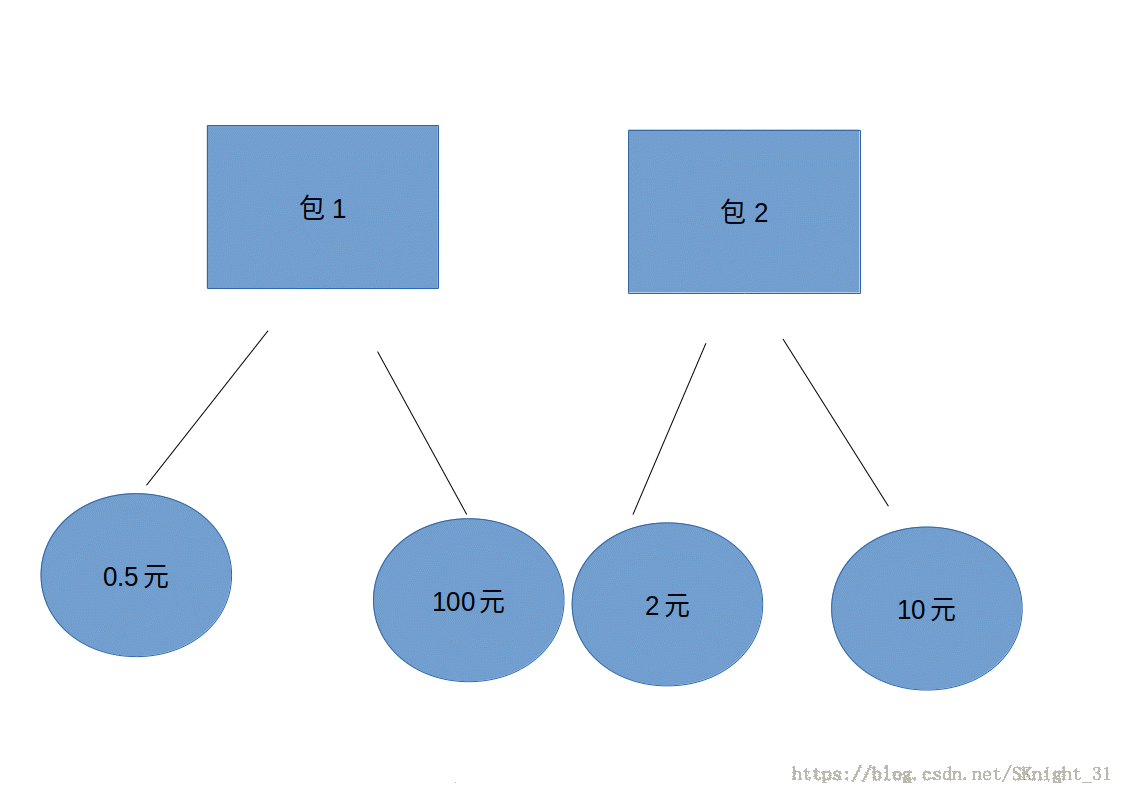
举个比较简单的例子。这里有两个包,在你知道两个包里有什么的情况下,你需要选一个包然后让你的竞争对手小明从这个包里的两张钱中选一张给你,但是你想让自己的钱越多越好而小明不想让你钱多,所以他会选一张相对最小的钱给你。也即对你而言,你需要从中获得最大利益,而小明只是想承受最小的对手变强程度。在这种情况下你应该选择包2,小明会给你2元。如果你选择了包1 ,你只能得到0.5元。
这其实就是极大极小搜索,抽象到树的形式来看,这次我们来选数字,注意一点的是这个树的搜索顺序用人脑其实是反过来的,这个具体我会在后面的代码实现里讲,为了方便我们理解就暂时先从下往上看把。就比如是上一题的包里拿钱问题,0.5,100是第一个包内的钱,2,10是第二个包里的,当我们拿了一个包就往上推让B选其中一张较小钱,即0.5或2,最后我们从这两张钱里选一张拿到我们手上,因为这是我们自己在推演这个过程,所以要考虑完备也即所有可能的情况,也就是为什么这里B可以选两张钱(这个说出来了就很好理解甚至有点蠢,但是我刚学的时候思路卡了很久所以提一下),这样在实际情况中其实我们只能选一个包让b选一张钱给我们,所以一个完备的推演过程可以保证我们获得的利益也就是最上面的节点的数字最大。其实分析以下我们可以推广到n层,无非是分成了两个层:一个是MAX层,这一层由我们来选择从下一层拿上来的数字,为了自己的利益最大化,我们会从下一层的子节点选择极大的一个来存在这个节点,故称为MAX;一个是MIN层,由对手选,同理,他会想方设法降低我们获得的利益,所以他会从下一层选极小的节点来存,这样我们的MAX层在选的时候就只能拿到相对较小的极大。
以上就是极大极小值搜索的内容了,但是单纯用极大极小搜索的意义不是很大,因为在博弈中,一步棋可能会有成千上万种招法,如果全部进行搜索时间耗费太长,效率不高,在规定时间内下棋肯定是行不通的。这个时候就需要进行一些优化,也就是阿尔法贝塔剪枝了。
小插曲:感兴趣的朋友还可以看看负极大值搜索这个算法,跟极大极小内涵一样,只是人们嫌转换极大极小不方便,干脆把极小层加个负号,这样可以全搜极大,因为极大的负就是这层的最小!这里不多说了。
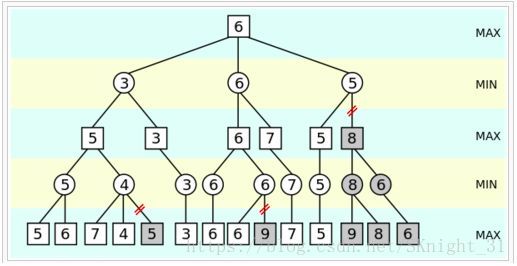
剪枝,顾名思义就是剪去枝节,也就是我们的树的节点链。【请务必先理解透彻极大极小的搜索逻辑和顺序!】下图引用自英文的阿尔法贝塔剪枝维基百科https://en.wikipedia.org/wiki/Alpha%E2%80%93beta_pruning
它和我们上面的选钱游戏的搜索树长得很像,因为这个算法就是基于极大极小值搜索的,为什么叫阿尔法贝塔,因为有alpha,beta两个值。alpha表示我们需要的最好结果,beta表示对手能承受的最坏结果。基于最坏的打算的思想,把alpha初值设为负无穷即-INF,beta为正无穷INF。上图是已经搜索完毕并且剪枝节了的,所以我们从下往上从左往右分析一下,为什么这样选,为什么这样剪枝。【其实最下面的MAX层我感觉没必要标出来,它们是已经先存在待选的】在最左边,选第一个MIN层即B选,对B而言研究beta,即B能承受的最小,拿下面两个子节点和beta比较,此时beta初值为-INF,一定小于子节点的数,选出了5是较小的,往上走发现第三层【从上往下数,后面也一样】的第一个节点有另一个子节点,于是去搜索另一个子节点,第五层第一个是7,返回到第四层第二个节点,然后继续往后,第五层第二个节点是4,比7小于是第四层第二个节点更新为4,此时出现了第一个剪枝【关键点来了!】。因为对于第三层第一个节点,我们已经搜过一次,得到此时的alpha是5,第三层是max层,他会从第四层对应子节点选一个极大的值,而第四层是min层会从第五层选择极小值,也就是说,我们继续在第五层的对应第四层第二个节点的子节点搜索也只可能返回给第四层第二个节点比4更小的数字,但是第三层选的是极大,5已经比4大了,换句话说,无论第四层第二个节点再怎么更新值也只能小于等于4,也即小于5,所以第三层第一个节点一定不会去选第四层第二个节点了,也就没有必要再搜索后面了,这就使用了第一次剪枝节。【记住一个关键点,考虑父节点的min、max性质,比较兄弟节点来剪枝节】第二次剪枝即第四层第五个节点剪枝同理不再讲。对于第三次剪枝节也即第二层第三个节点,我们先搜索他的第一个子节点,一路搜上来返回了5,这里直接剪掉了一整条第三层第六节点。这里从我上面提到的关键点考虑,因为第一层是max层,他会从第二层选一个极大,此时我们已经搜索出来第二层第二个节点是6,而第三个节点是5,第二层是min层,第三个节点继续搜索也只可能比5小,也即小于6,所以直接剪去第二层第三节点的所有其他子节点,去搜索第四个节点【如果有的话】。
【为方便阅读看图下面再贴一次】
相信到这里大家应该已经对概念理解的差不多了。上面我曾提到过,为了方便理解,我们从底部往上想,但是在代码里这样就不太好写了。对代码,我们可以利用递归返回来实现从下往上回溯,返回一个一个的节点搜索值。递归如果你比较熟悉的话应该会容易懂,即写的时候是从上往下写,但逻辑上其实是从下往上返回值。
先推荐一个我感觉alpha-beta写的比较清楚的:https://blog.csdn.net/u013351484/article/details/50810224
这个是一个三角点格棋的题,理解这个存储局面和连边可能会有点挫折,实在看不明白可以直接看他的alpha-beta函数,不去理会这个题本身,博主注释写的还是很清楚的!欢迎评论留言
这篇关于对极大极小搜索和阿尔法贝塔剪枝搜索算法的简单描述与理解--萌新向通俗易懂的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!