[西瓜书笔记] CH1绪论CH2模型评估与选择

本文主要是介绍[西瓜书笔记] CH1绪论CH2模型评估与选择，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

第一章绪论

机器学习：
- 计算的手段
- 自身经验(数据)
- 改善性能(学习算法→模型)
属性空间={属性1，属性2，…}
分类
泛化(generalization)：适用于新样本的能力
模型应注重于预测未知，拟合未知
独立同分布i.i.d
归纳：所有匹配的假设→假设空间→版本空间
归纳偏好（优先考虑实际业务）

第二章模型的评估与选择

error rate：错误率 E=a/m
accuracy：精度 1-a/m
误差error：
- 训练集→训练误差经验误差
- 新样本→泛化误差【目标：减小泛化误差】
拟合，过拟合overfitting，欠拟合underfitting
验证集应尽可能与训练集互斥
用测试集上的判别效果来估计模型在实际使用时的泛化能力，而把训练数据另外划分为训练集和验证集，基于验证集上的性能来进行模型选择和调参。

▲模型评估方法：

留出法(hold-out)：将数据集划分为两个互斥的集合，一个用于训练S，一个用于验证T。D=S \cup T，S \cap T = \emptset
- 保持样本类别比例相似 → 分层采样stratified sampling
- 若干次随机划分、重复实验后取平均值作为评估结果
- 缺点：S过多，T较小，评估结果不稳定准确；T过多，评估模型会和D训练出的模型有较大差别，降低评估结果的保真性
- 常见解决做法：2/3 - 4/5用于训练，剩余用于验证
k折交叉验证法(k-fold cross validation)：将数据集D划分为k个大小相似的互斥子集，每个子集都尽可能保持数据分布的一致性。每次用k-1个子集的并集作为训练集，剩余的一个子集作为验证集。进行k次训练和验证，返回k个验证结果的均值。
- 常用k=10，其次为5、20
- 为减少样本划分不同引入的区别，随机使用不同的划分进行p次k折交叉验证
- 特例：当k=数据集D样本数，留一法(Leave-One-Out,LOO)。用留一法实际评估的模型与期望评估用D训练出的模型相似（，但是数据量大时开销过大。
自助法(bootstrapping)：每次随机从D中挑选一个样本将其拷贝放入D’ ，然后再将该样本放回初始数据集D中，使得该样本在下次采样时仍有可能被采到;这个过程重复执行m 次后，我们就得到了包含 m 个样本的数据集 D’。
- 有1/3的数据不会在训练集中出现
- 适用于数据集较小、难以有效划分训练验证集的场合；初始数据集产生多个不同的训练集，利于集成学习
- 会引入估计偏差

▲性能度量(performance measure)：

衡量模型泛化能力的评价标准，反映了任务需求
回归任务：均方误差(mse)
分类任务：
1. 错误率和精度
2. 查准率percision、查全率recall、F1：
  - TP+FP+TN+FN=样本总数
  
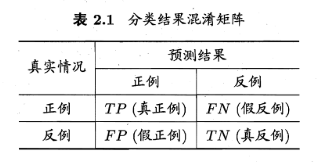
  - 查准率P=TP/(TF+FP)
  - 查全率R=TP/(TP+FN)
  - 查准率和查全率是矛盾的
  - P-R曲线：若一个学习器的P-R曲线被另一个学习器的曲线完全"包住" ，则可断言后者的性能优于前者；若发生交叉难以断言有了程度。
  - 平衡点(Break-Event Point,BEP)：查准率=查全率。两个学习器之间，若A的平衡点大于B的平衡点，那么学习器A优于B
  - F1度量：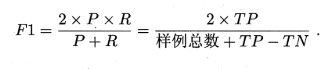
  - 由于不同场景对查准率和查全率重视程度不同，F1度量的一般形式表达对查准率和查全率不同的偏好。\beta=1, F_\beta = F1; \beta>1, 查全率有更大影响；\beta<1,查准率有更大影响。
  
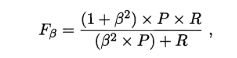
  - 多次训练/验证得到多个二分类混淆矩阵，为了综合考察查准率和查全率，有几种做法：①分别计算P和R，再计算平均值，得到宏查准率marco-P、宏查全率、宏F1 ；② 先将混淆矩阵对应元素进行平均，得到TP、FP、TN、FN的平均值，再基于平均值计算微查准率、微查全率、微F1。