本文主要是介绍（CQL）Conservative Q-Learning for Offline Reinforcement Learning，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
Abstract
\qquad 在大规模、现实世界应用中，强化学习如何有效利用庞大的、历史收集的 datasets 是一个关键挑战。 O f f l i n e R L Offline\; RL OfflineRL 算法旨在利用 p r e v i o u s l y − c o l l e c t e d previously-collected previously−collected、 s t a t i c d a t a s e t s w i t h o u t f u r t h e r i n t e r a c t i o n static \; datasets\; without \; further \; interaction staticdatasetswithoutfurtherinteraction 学习有效的策略。然而，在实践中， O f f l i n e R L Offline\; RL OfflineRL 代表了一个主要的挑战，标准的 o f f − p o l i c y R L off-policy RL off−policyRL 算法可能由于 d a t a s e t dataset dataset 和 l e a r n e d p o l i c y learned policy learnedpolicy 之间的分布差异 导致的过估计而失效，尤其是当在一个 c o m p l e x complex complex 、 m u t i − m o d a l d a t a d i s t r i b u t i o n s muti-modal \; data \; distributions muti−modaldatadistributions 上训练时。
\qquad 在本文中，我们提出了 c o n s e r v a t i v e Q − l e a r n i n g ( C Q L ) conservative \; Q-learning (CQL) conservativeQ−learning(CQL)，旨在学习一个保守的 Q − f u n c t i o n Q-function Q−function，即通过该 Q − f u n c t i o n Q-function Q−function 得到的值是其真实值的下界。
\qquad 我们从理论上证明了CQL产生了一个当前策略的价值的下界，它是一个有 t h e o r e t i c a l i m p r o v e m e n t g u a r a n t e e s theoretical \; improvement \; guarantees theoreticalimprovementguarantees 的 p o l i c y l e a r n i n g p r o c e d u r e policy \; learning \; procedure policylearningprocedure（ 策略学习过程 ） 。在实践中，CQL通过一个简单的 Q − v a l u e r e g u l a r i z e r Q-value \; regularizer Q−valueregularizer 对标准Bellman误差目标进行了扩展，该正则化器在现有 deep q-learning 和actor-critic实现之上易于实现。在离散和连续控制领域，我们表明CQL实质上优于现有的离线RL方法，通常学习策略获得2-5倍的高最终回报，特别是在学习复杂和多模态数据分布时。
3、The Conservative Q-Learning (CQL) Framework
\qquad 我们提出了一个 c o n s e r v a t i v e Q − l e a r n i n g ( C Q L ) conservative \; Q-learning (CQL) conservativeQ−learning(CQL) 算法，通过这个算法学习到的一个 p o l i c y policy policy 的 Q − f u n c t i o n Q-function Q−function 的期望值是其真实值的下界。 Q − v a l u e Q-value Q−value 的下界可以防止 O f f l i n e R L Offline\; RL OfflineRL 设置中常见的由于OOD动作和函数逼近错误而导致的过高估计[36,32]。我们使用 C Q L CQL CQL 泛指Q-learning方法和actor-critic方法，尽管后来也使用明确的策略。我们首先关注 C Q L CQL CQL 中的策略评估步骤，它本身可以作为一个非策略评估过程使用，或者集成到一个完整的 O f f l i n e R L Offline\; RL OfflineRL 算法中，我们将在3.2节中讨论。
3.1 Conservative Off-Policy Evaluation
\qquad 我们想估计 在行为策略 π β ( a ∣ s ) \pi_{\beta}(a|s) πβ(a∣s) 下生成的数据集 D D D 中的 t a r g e t p o l i c y π target \; policy\; \pi targetpolicyπ 的 价值 V π ( s ) \; V^{\pi}(s) Vπ(s) 。因为我们注重防止对策略值的过高估计，所以我们想学习一个 保守的下界 Q − f u n c t i o n Q-function Q−function，在最小化 s t a n d a r d B e l l m a n e r r o r o b j e c t i v e standard \; Bellman \; error \; objective standardBellmanerrorobjective 的同时，最小化 Q − v a l u e Q-value Q−value。我们选择的惩罚项是，最小化在特定 s t a t e − a c t i o n p a i r s state-action \; pairs state−actionpairs 分布下 Q − v a l u e Q-value Q−value 的期望。由于标准的 Q − f u n c t i o n Q-function Q−function 训练不查询 未观测 s t a t e state state 的 Q − f u n c t i o n Q-function Q−function，但是查询 未观测 a c t i o n action action的 Q − f u n c t i o n Q-function Q−function。我们限制 μ \mu μ 来与数据集中的 state-marginal 匹配，即 μ ( s , a ) = d π β μ ( a ∣ s ) \mu(s,a) = d^{\pi_{\beta}}\mu(a|s) μ(s,a)=dπβμ(a∣s)。这样就可以进行训练过程中 Q − f u n c t i o n Q-function Q−function 的迭代更新：
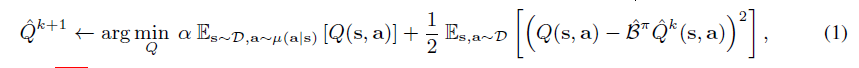
\qquad 其中 α \alpha α 是权衡因子。
\qquad 在 T h e o r e m 3.1 Theorem\;3.1 Theorem3.1 中，我们展示了 对于所有的 ( s , a ) (s,a) (s,a) ， Q − f u n c t i o n Q-function Q−function 是 Q π Q^\pi Qπ 的下界：
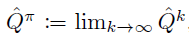
\qquad 然而，如果只想估计 V π ( s ) V^\pi(s) Vπ(s) ，我们可以大幅收紧这个下界。如果我们需要 π ( a ∣ s ) \pi(a|s) π(a∣s) 下的 Q π ^ \hat{Q_{\pi}} Qπ^的期望是 V π ( s ) V^\pi(s) Vπ(s) 的下界，我们可以通过引入一个额外的 data 分布 π β ( a ∣ s ) \pi_{\beta}(a|s) πβ(a∣s) 下的 Q − v a l u e m a x i m i z a t i o n t e r m Q-value \; maximization \; term Q−valuemaximizationterm 来提升这个上界。迭代更新公式为：
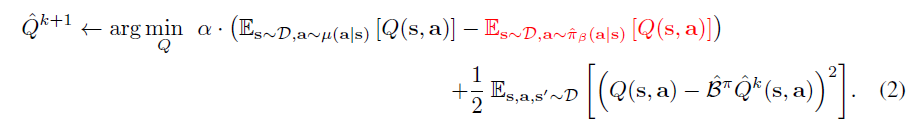
\qquad 在 T h e o r e m 3.2 Theorem\;3.2 Theorem3.2 中，我们展示了 结果 Q − v a l u e Q ^ π Q-value \; \hat{Q}_{\pi} Q−valueQ^π 不是 a point-wise lowerbound，当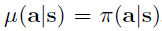
的时候有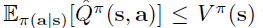
。直观上，公式（2）在最大化行为策略 π ^ β \hat{\pi}_{\beta} π^β下的 Q − v a l u e Q-value Q−value 时， π ^ β \hat{\pi}_{\beta} π^β下的动作的 Q − v a l u e s Q-values Q−values 更可能被过估计，因此 Q ^ π \hat{Q}^{\pi} Q^π 不一定是 Q π Q^{\pi} Qπ 的 pointwise 下界。而最大化项中原则上可以利用除了 π ^ β ( a ∣ s ) \hat{\pi}_{\beta}(a|s) π^β(a∣s) 的其他分布，我们在附录D.2中证明了结果值不能保证是其他分布的下界。
\qquad 公式（1）展示了基础的 CQL 公式，学到的 Q − f u n c t i o n Q-function Q−function 是真是 Q − f u n c t i o n Q π Q-function \; Q^{\pi} Q−functionQπ 的下界，公式（2）展示了 e x p e c t e d Q − v a l u e o f t h e p o l i c y expected \; Q-value \; of \; the \; policy expectedQ−valueofthepolicy 的更 t i g h e r tigher tigher 的下界。通过选择比较好的 α \alpha α 两个公式都可行，一般 α \alpha α 设置的比较小。
3.2 Conservative Q-Learning for Offline RL
\qquad 将结果应用于一个 c o m p l e t e R L a l g o r i t h m complete \; RL \; algorithm completeRLalgorithm
\qquad 提出 o f f l i n e p o l i c y l e a r n i n g offline \; policy \; learning offlinepolicylearning 的一般化方法 —— c o n s e r v a t i v e Q − l e a r n i n g ( C Q L ) conservative \; Q-learning \; (CQL) conservativeQ−learning(CQL)
\qquad
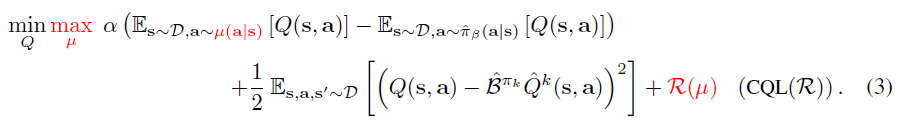
这篇关于（CQL）Conservative Q-Learning for Offline Reinforcement Learning的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
