动态规划---------矩阵连乘

动态规划实现矩阵连乘问题

一、动态规划

动态规划和分治法十分相似，动态规划的基本思想是将待求解的问题分解为若干子问题的解得到原问题的解。动态规划算法通常适用于求解最优化问题。
动态规划的步骤如下：
1、找出最优解的性质，并刻画其结构特征。
2、递归地定义最优值。
3、以自底向上的方式计算最优值。
4、根据计算的最优值时得到的信息，构造最优解。

二、矩阵连乘问题

问题描述：给定n个矩阵：A1,A2,…,An，其中Ai与Ai+1是可乘的，i=1，2…，n-1。确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。

思路：矩阵连乘可以通过添加括号来改变矩阵相乘时候的顺序，从而改变最终相乘的次数，所以我们只需要找到最优的添加括号的方式就能求出矩阵相乘时次数最少的那次。利用的是自底向上的方式。

对于两个矩阵相乘A1*A2，A1为p✖q矩阵，A2为q✖r矩阵，（两个矩阵可以相乘必须满足第一个矩阵的列数等于第二个矩阵的行数），两者相乘共需要p✖q✖r次。

我们将矩阵连乘Ai*Ai+1…*Aj，简记为A[i:j],所以我们需要求得就是A[i:n]的最优计算次序；假设矩阵A[i:j]（1<=i<=j<=n）所需要的最少相乘次数为m[i][j]，则对于A[1:n]的最优值为m[1][n]。
1.当i=j时，A[i][j]=A[i][i]=Ai为单一矩阵，相乘次数为0，m[i][j]=m[i][i]=0（i= 1，2，3…）
2.当i<j时，可以利用最优子结构性质来计算m[i][j]。事实上，若A[i:j]的最优次序在Ak和Ak+1之间断开，i<=k<j,则：m[i][j]=m[i][k]+m[k+1][j]+pi-1pkpj。由于在计算是并不知道断开点k的位置，所以k还未定。不过k的位置只有j-i个可能。因此，k是这j-i个位置使计算量达到最小的那个位置。

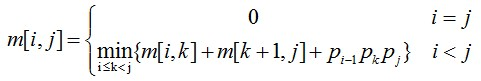
**3.**计算最优解：

void MatrixChain(int *p,int n,int m[][100],int s[][100])
{int i,r,j,k;for(i=1;i<=n;i++)//i要从1开始m[i][i]=0;//将对角线的位置全部置为0for(r=2;r<=n;r++)//自底向上开始，从两个矩阵相乘一直到n个矩阵相乘{for(i=1;i<=n-r+1;i++){j = i+r-1;//矩阵相乘结束的位置m[i][j] = m[i+1][j]+p[i-1]*p[i]*p[j];//m[i][j] =m[i][i]+m[i+1][j]+p[i-1]*p[i]*[j];等于上面的因为m[i][i]的值就为0s[i][j]=i;//存放断点的位置for(k=i+1;k<j;k++)//寻找最优值，并且把它放在m[i][j]的位置{int t = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];if(t<m[i][j])//找最小的{m[i][j] = t;//最优值重置为ts[i][j] = k;//断点位置重置为k}}}}
}

4.构造最优解：

void Traceback(int i,int j,int s[][100])//构造最优解
{if(i == j){cout<<"A"<<i;return ;}cout<<"(";Traceback(i,s[i][j],s);Traceback(s[i][j]+1,j,s);cout<<")";
}

最后填表的问题是：先填写主对角线上的然后依次向上一斜行填写。

三、代码展示

#include<iostream>
using namespace std;
int m[100][100];//用于存放最优值
int s[100][100];//用于存放断点的位置
void MatrixChain(int *p,int n,int m[][100],int s[][100])
{int i,r,j,k;for(i=1;i<=n;i++)//i要从1开始m[i][i]=0;//将对角线的位置全部置为0for(r=2;r<=n;r++)//自底向上开始，从两个矩阵相乘一直到n个矩阵相乘{for(i=1;i<=n-r+1;i++){j = i+r-1;//矩阵相乘结束的位置m[i][j] = m[i+1][j]+p[i-1]*p[i]*p[j];//m[i][j] =m[i][i]+m[i+1][j]+p[i-1]*p[i]*[j];等于上面的因为m[i][i]的值就为0s[i][j]=i;//存放断点的位置for(k=i+1;k<j;k++)//寻找最优值，并且把它放在m[i][j]的位置{int t = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];if(t<m[i][j])//找最小的{m[i][j] = t;//最优值重置为ts[i][j] = k;//断点位置重置为k}}}}
}
void Traceback(int i,int j,int s[][100])//构造最优解
{if(i == j){cout<<"A"<<i;return ;}cout<<"(";Traceback(i,s[i][j],s);Traceback(s[i][j]+1,j,s);cout<<")";
}
int main()
{int p[100];//用于存放矩阵的行数和列数int n,i;cout<<"Input n"<<endl;cin>>n;cout<<"请输入矩阵的行号和列号："<<endl;for(i=0;i<n;i++)cin>>p[i];cout<<"最优顺序为："<<endl;MatrixChain(p,n-1,m,s);Traceback(1,n-1,s);cout<<endl;return 0;
}