本文主要是介绍# [cs231n (六)神经网络 part 2:传入数据和损失 ][1],希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
cs231n (六)神经网络 part 2:传入数据和损失
标签(空格分隔): 神经网络
文章目录
- [cs231n (六)神经网络 part 2:传入数据和损失 ][1]
- 同类文章
- 0.回顾
- 1. 引言
- 2. 初始化数据和模型
- 1. 数据预处理阶段
- **处理方式:**
- **白化和PCA**
- 2. 权重初始化
- 3.批归一化
- 4. 正则化
- 3. 损失函数
- 4. 总结
- 转载和疑问声明
- 我祝各位帅哥,和美女,你们永远十八岁,嗨嘿嘿~~~
同类文章
cs231n (一)图像分类识别讲了KNN
cs231n (二)讲了线性分类器:SVM和SoftMax
cs231n (三)优化问题及方法
cs231n (四)反向传播
cs231n (五)神经网络 part 1:构建架构
cs231n (六)神经网络 part 2:传入数据和损失
cs231n (七)神经网络 part 3 : 学习和评估
cs231n (八)神经网络总结:最小网络案例研究
cs231n (九)卷积神经网络
0.回顾
cs231n (一)图像分类识别讲了KNN
cs231n (二)讲了线性分类器:SVM和SoftMax
cs231n (三)优化问题及方法
cs231n (四)反向传播
cs231n (五)神经网络(part 1) 构建架构
1. 引言
五系列我们讲了神经元模型,主要是加个激活函数,然后定义损失,然后梯度下降。
2. 初始化数据和模型
这里主要是数据预处理、权重初始化啦、还有损失函数的构建,优化问题不要着急哈。
1. 数据预处理阶段
这个可是很重要的级阶段,就像你做饭,食材是很重要的。
基本术语和符号:数据矩阵X = [NxD] = 100x3072
处理方式:
-
减去均值,一般也称作去中心化:想象一个数据云图,就是把他们移到原点
实现代码:X -= np.mean(X, axis=0),或者 X -= np.mean(X) -
归一化数据, 将维度中心化,就是让大家相差不太,数值近似相等
实现方法:
- 先对数据零中心化,然后除以标准差:
X /= np.std(X, axis=0) - 对每个维度都做归一化,使得他们范围一致【-1,1】,适用于:数据特征的计算单位不一样。
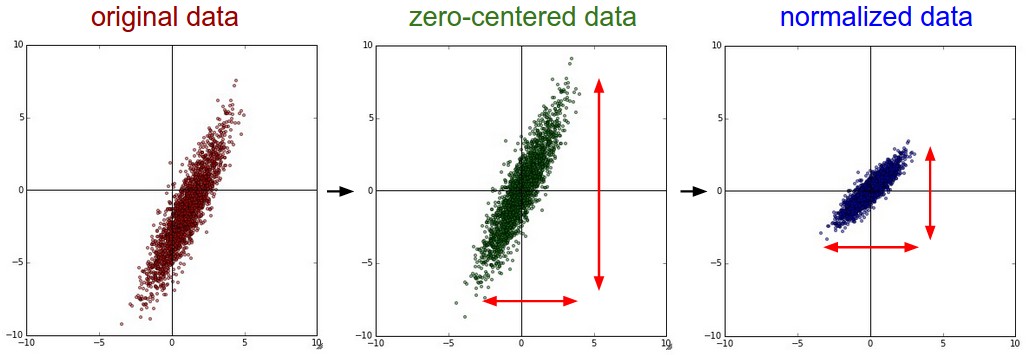
上述预处理方法可以从这里看出:左 原始数据,中:减去均值方法,右:除以标准差之后的
白化和PCA
主要方法:先对数据零中心化,然后计算协方差矩阵。
# 输入数据矩阵X = [N x D]
X -= np.mean(X, axis = 0) # 进行零中心化 重点
cov = np.dot(X.T, X) / X.shape[0] # 得到协方差矩阵
协方差矩阵是什么? 第(i,j)的元素就是第i个数据的j维度的协方差,矩阵的对角线上是元素的方差,我们可以对协方差矩阵进行SVD奇异值分解
U,S,V = np.linalg.svd(cov)
其中 U的列是特征向量,S 是含有奇异值的1维数组,为达到去除数据的相关性,我们把去零中心化的数据投影到特征基上
Xrot = np.dot(X,U) # 去相关性
np.linalg.svd的返回值U中,特征向量是按照特征值的大小排列的,这样就可以进行数据降维了俗称主成分分析PCA,详细内容可以查看我的博客。
Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced 变成了 [N x 100]
这样原始数据就降维到了 Nx100
接下来说一下白化,输入:特征基准上的数据,对每个维度除以其特征值实现归一化。
因为数据一般是符合高斯分布的,白化后,那么得到均值是零,协方差是相等的矩阵。
Xwhite = Xrot / np.sqrt(S + 1e-5),这里添加了1e-5是防止分母是零情况
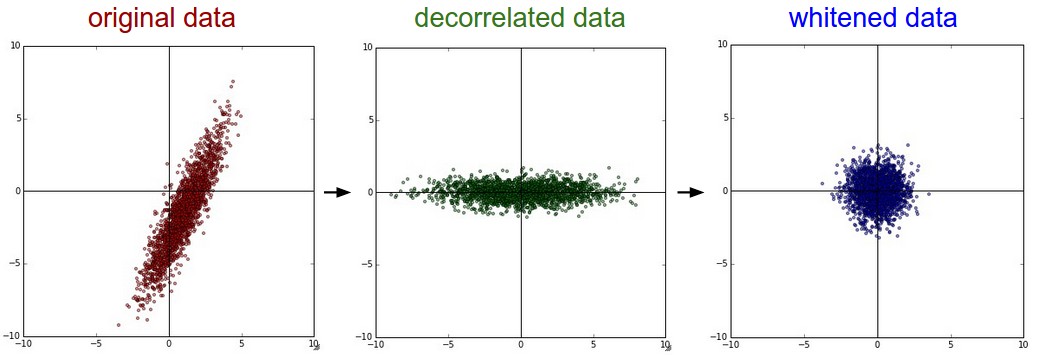
依次是:原始,PCA, 白化后的数据。
可以看看对于实际数据预处理之后的样子。

左:原始数据,中:3072特征值向量的最大的144,右:PCA降维后的数据,右右:白化数据
注意的是:我们一般是在训练集上进行数据进行预处理,验证和测试集减去的是训练数据均值
2. 权重初始化
训练前我们是没有权重的怎么办?
随机啊 !聪明! 你简直就是个天才,看看爱因斯坦怎么说的吧
全零肯定不行
-
随机数(比较小的)
W = 0.01 * np.random.randn(D,H), 想想嘛,数值太小,梯度又穿不透很深的网络,还有有一定问题滴,随着输入数据量的增长,随机初始化的神经元的输出数据的分布中的方差也在增大 -
1/sqrt(n)校准方差 :
w = np.random.randn(n) / sqrt(n), n是输入数据的数量, -
稀疏初始化,权重矩阵设为零,神经元随机链接,不好不好。
-
偏置初始化,一般是零, 至于其他的你可以多尝试呗。
3.批归一化
批量归一化:在网络的每一层之前都做预处理,只不过是以另一种方式与网络集成在了一起
4. 正则化
上节内容已经说过了,就是用来防止过拟合的常见的有:
- L2正则化:就是二范数,就是$ \frac{1}{2}\lambda w^2$
- L1正则化:就是一范数,其实就是 $ \lambda_1|w|+\lambda_2w^2 $
- 最大范式约束:加一个限制: ∣ ∣ w → ∣ ∣ 2 < c ||\overrightarrow{w}||_2<c ∣∣w∣∣2<c 就算学习率很大也不会出现数值爆炸。
- 随机死亡:dropout: 来源于这里
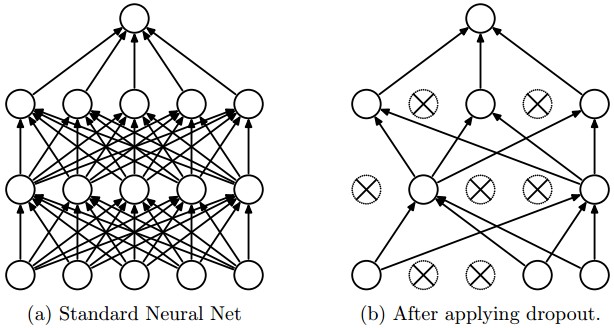
""" Vanilla Dropout: Not recommended implementation (see notes below) """p = 0.5 # probability of keeping a unit active. higher = less dropoutdef train_step(X):""" X contains the data """# forward pass for example 3-layer neural networkH1 = np.maximum(0, np.dot(W1, X) + b1)U1 = np.random.rand(*H1.shape) < p # first dropout maskH1 *= U1 # drop!H2 = np.maximum(0, np.dot(W2, H1) + b2)U2 = np.random.rand(*H2.shape) < p # second dropout maskH2 *= U2 # drop!out = np.dot(W3, H2) + b3# backward pass: compute gradients... (not shown)# perform parameter update... (not shown)def predict(X):# ensembled forward passH1 = np.maximum(0, np.dot(W1, X) + b1) * p # NOTE: scale the activations (要乘上p)H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # NOTE: scale the activationsout = np.dot(W3, H2) + b3实际更多使用反向随机失活(inverted dropout)
"""
Inverted Dropout: Recommended implementation example.
We drop and scale at train time and don't do anything at test time.
"""p = 0.5 # probability of keeping a unit active. higher = less dropoutdef train_step(X):# forward pass for example 3-layer neural networkH1 = np.maximum(0, np.dot(W1, X) + b1)U1 = (np.random.rand(*H1.shape) < p) / p # first dropout mask. Notice /p!H1 *= U1 # drop!H2 = np.maximum(0, np.dot(W2, H1) + b2)U2 = (np.random.rand(*H2.shape) < p) / p # second dropout mask. Notice /p!H2 *= U2 # drop!out = np.dot(W3, H2) + b3# backward pass: compute gradients... (not shown)# perform parameter update... (not shown)def predict(X):# ensembled forward passH1 = np.maximum(0, np.dot(W1, X) + b1) # no scaling necessaryH2 = np.maximum(0, np.dot(W2, H1) + b2)out = np.dot(W3, H2) + b3
3. 损失函数
前面我们已经学过了 SVM and Softmax
L i = ∑ j ≠ y i m a x ( 0 , f j − f y i + 1 ) \displaystyle L_i=\sum_{j\not=y_i}max(0,f_j-f_{y_i}+1) Li=j=yi∑max(0,fj−fyi+1)
L i = − l o g ( e f y i ∑ j e f j ) \displaystyle L_i=-log(\frac{e^{f_{y_i}}}{\sum_je^{f_j}}) Li=−log(∑jefjefyi)
标签数目很大怎么办? 使用softmax分层,
回归问题:预测实数的值的问题,预测房价,预测图片东西的长度
对于这种问题,计算预测值和真实值之间的损失就够了。
然后用L2平方范式或L1范式取相似度 L i = ∣ ∣ f − y i ∣ ∣ 2 2 L_i=||f-y_i||^2_2 Li=∣∣f−yi∣∣22
4. 总结
直接看目录不就知道了哇,哈哈。
预处理————正则化方法————损失函数
转载和疑问声明
如果你有什么疑问或者想要转载,没有允许是不能转载的哈
赞赏一下能不能转?哈哈,联系我啊,我告诉你呢 ~~
欢迎联系我哈,我会给大家慢慢解答啦~~~怎么联系我? 笨啊~ ~~ 你留言也行
你关注微信公众号1.机器学习算法工程师:2.或者扫那个二维码,后台发送 “我要找朕”,联系我也行啦!

(爱心.gif) 么么哒 ~么么哒 ~么么哒
码字不易啊啊啊,如果你觉得本文有帮助,三毛也是爱!
我祝各位帅哥,和美女,你们永远十八岁,嗨嘿嘿~~~


这篇关于# [cs231n (六)神经网络 part 2:传入数据和损失 ][1]的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



