控制教程 —— 巡航控制篇：1.系统建模及开环响应分析

物理模型建立

在现代车辆的反馈控制系统中，自动巡航控制一个典型的例子。巡航控制系统的目的是在不受外界干扰(如风或坡度变化)的情况下保持恒定的车速。可以通过测量测速，将其与期望速度或参考速度进行比较，并根据控制规律自动调节油门来实现。

这里我们考虑一个简单的车辆动力学模型，如上面的受力分析图。质量为m的车辆收到控制力u的作用，作用力u表示在道路/轮胎面产生的力，对于这个简化的模型，我们将假定我们可以直接控制该力，而忽略产生该力的动力总成，轮胎等影响。假定由于滚动摩擦和风阻而产生的阻力bv随车速v线性变化，作用方向与车辆运动方向相反。

系统动力方程式

基于以上假设，我们可以建立一阶质量阻尼器系统，沿x方向求和应用牛顿第二定律，我们得出以下系统方程：
$$m\dot{v}+bv=u$$由于我们对控制车辆的速度感兴趣，因此输出方程选择如下：
$$y=v$$

系统参数配置

对于上述例子，我们假设系统的参数为：
m 车辆质量 1000 kg
b 阻尼系数 50 N.s/m
u 额定控制力 500 N

状态空间模型

一阶系统只有一种能量存储模式，该例子中是汽车的动能，因此只需要一个状态变量，即速度。因此，状态空间表示为：
$$\dot{\mathbf{x}}=[\dot{v}]=\left[\frac{-b}{m}\right][v]+\left[\frac{1}{m}\right][u]$$$$y=[1][v]$$我们使用以下命令将状态空间模型输入到MATLAB中：

m = 1000;
b = 50;A = -b/m;
B = 1/m;
C = 1;
D = 0;cruise_ss = ss(A,B,C,D);

传递函数模型

将控制微分方程进行拉普拉斯变换，并假设零初始条件，可以得到巡航控制系统的传递函数为：
$$P(s)=\frac{V(s)}{U(s)}=\frac{1}{ms+b}[\frac{m/s}{N}]$$我们使用以下命令将传递函数模型输入到MATLAB中：

s = tf('s');
P_cruise = 1/(m*s+b);

控制指标设计

现在为系统设计控制指标，当发动机提供500 N的力时，汽车将达到 10 m/s的最大速度，现在设计汽车在不到 5s 的时间内加速达到该速度，在本应用中，速度上 10% 的超调和 2% 的稳态误差就可以满足要求。
因此我们对该系统提出了以下设计标准：

• 上升时间 < 5s
• 超调 < 10%
• 稳态误差 < 2%

开环阶跃响应

在MATLAB中模拟该系统在没有反馈控制的情况下对 500N 的阶跃作用力的开环响应：

m = 1000;
b = 50;
u = 500;s = tf('s');
P_cruise = 1/(m*s+b);step(u*P_cruise)

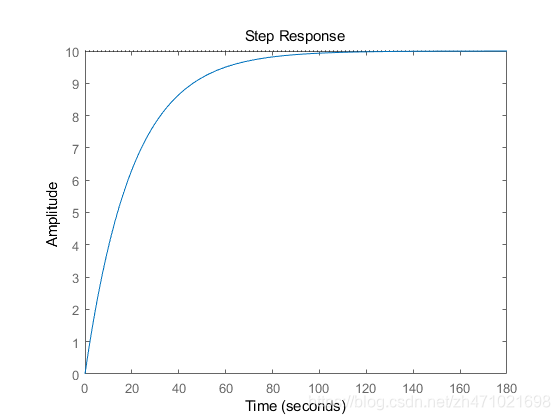
我们可以看到，开环系统没有过冲和振荡(一阶系统的特性)，并且确实达到了所需的 10m/s 的稳态速度。但是，上升时间太慢，约 60s。因此，我们需要设计一种反馈控制器，该控制器在不对其他动态性能指标产生不利影响的情况下加快响应速度。

开环极点/零点

巡航控制系统在 $s=-b/m$ 处具有一个单极点，我们可以使用以下命令在 s 平面上绘制该极点。

pzmap(P_cruise)
axis([-1 1 -1 1])

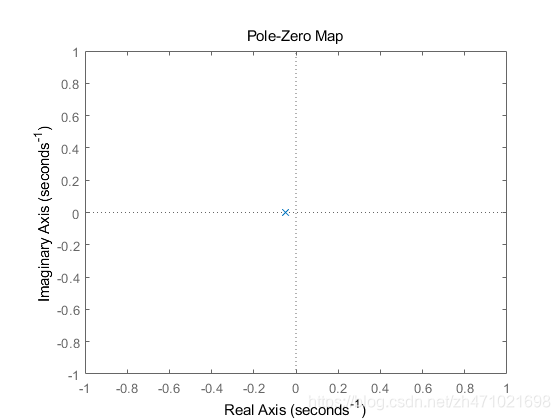
我们观察到开环系统是稳定的，不会振荡，因为极点是负实数。此外，响应速度由该极点的幅度 $b/m$ 决定：幅度越大，系统越快达到稳态值，由于通常无法更改系统参数来改变系统的动态响应，因此必须设计控制器来调整闭环系统的极点和零点，来满足所需的性能指标。

开环伯德图

我们还可以使用以下命令来绘制系统的开环频率响应图：

bode(P_cruise)

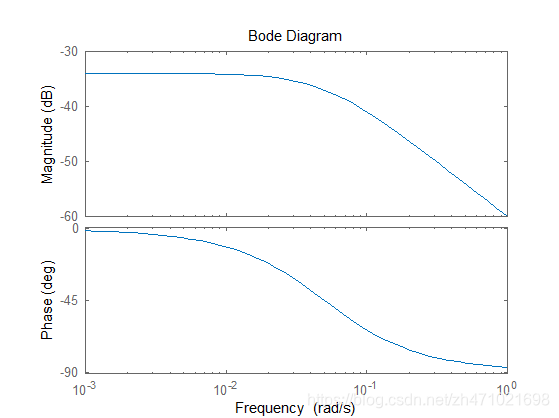
我们可以看到，伯德图显示了一阶系统的特征。