本文主要是介绍cs224w 图神经网络 学习笔记(二)Properties of Networks and Random Graph Models,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
课程链接:CS224W: Machine Learning with Graphs
课程视频:【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)
目录
- 1. How to measure a Network?——网络的属性
- 2. 一些真实网络案例的属性计算
- 2.1 MSN Messager网络
- 2.2 PPI网络(蛋白质相互作用的网络)
- 3. 最简单的图模型——ER Random Graph Model (ER随机图模型)
- 4. 小世界网络模型 The Small-world model
- 5. Kronecker Graph Model——Generating large realistic graphs
1. How to measure a Network?——网络的属性
1.1 度分布(Degree distribution) P ( k ) P(k) P(k)
度分布 P ( k ) P(k) P(k)是指,网络中,度为 k k k的节点的出现概率;对于有向图来说又分为入度分布和出度分布。如果网络中总共有 N N N个节点,其中有 N k N_k Nk个节点,他的度为 k k k,那么
P ( k ) = N k N w h e r e N k = nodes with degree k P(k)=\frac {N_k}{N} \quad where \quad N_k= \text{nodes with degree k} P(k)=NNkwhereNk=nodes with degree k

1.2. 路径长度 h h h
路径是一个节点序列,其中每个节点都链接到下一个节点。(A path is a sequence of nodes in which each node is linked to the next one)。路径可以重复经过节点和边;在有向图里面,路径的方向必须要沿着箭头的方向。
有了路径的概念,就可以定义图中两个点之间的距离(distance)。距离即最短路径,如果两个节点不相连,则通常会将这两个节点之间的距离定义为 h = ∞ h=\infty h=∞或者 h = 0 h=0 h=0。
在此基础上,可以定义图的直径(diameter)——The maximum (shortest path) distance between any pair of nodes in a graph,即图中节点距离的最大值。
对于连通图或者强连通有向图来说,图的平均路径长度(Average path length)可以由下面这个式子计算:
h ‾ = 1 2 E m a x ∑ i , j ≠ 1 h i j \overline{h}=\frac{1}{2E_{max}}\sum_{i,j \neq 1}{h_{ij}} h=2Emax1i,j=1∑hij
其中 h i j h_{ij} hij是节点 i i i和节点 j j j之间的距离, E m a x = n ( n − 1 ) / 2 E_{max}=n(n-1)/2 Emax=n(n−1)/2是图中的最大边数。通常情况下,在计算时我们会忽略不相连的节点之间的距离。
1.3. 聚类系数(Clustering coefficient) C C C
参考资料:聚类系数的含义和计算
在图论中,集聚系数(也称群聚系数、集群系数)是用来描述一个图中的顶点之间结集成团的程度的系数。
对于图中的节点 i i i来说,其聚类系数 C i ∈ [ 0 , 1 ] C_i \in [0,1] Ci∈[0,1]。在计算聚类系数时,找出其直接邻居节点集合 N i N_i Ni,计算 N i N_i Ni构成的网络中的边数 k k k,除以 N i N_i Ni集合中可能存在的边数 ∣ N i ∣ ∗ ∣ N i − 1 ∣ / 2 |N_i|*|N_i-1|/2 ∣Ni∣∗∣Ni−1∣/2。即:
C i = n C k 2 = 2 e i k i ( k i − 1 ) C_i=\frac {n}{C{^2_k}}=\frac {2e_i}{k_i(k_i-1)} Ci=Ck2n=ki(ki−1)2ei
其中 e i e_i ei表示节点 i i i的邻居节点构成的边, k i k_i ki表示节点 i i i的度, k i ( k i − 1 ) k_i(k_i-1) ki(ki−1)是节点 i i i的邻居节点所能相连的最大的边的数量。
| 图 | 聚类系数计算 |
|---|---|
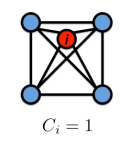 | 对于节点 i i i来说,邻居节点一共有4个,这4个邻居节点构成了6条边,他们所有可能构成的边为 C 4 2 = 4 × 3 2 = 6 C{^2_4}=\frac {4 \times 3} {2}=6 C42=24×3=6因此其聚类系数为 C i = 6 6 = 1 C_i=\frac {6}{6}= 1 Ci=66=1 |
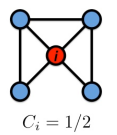 | 对于节点 i i i来说,邻居节点一共有4个,这4个邻居节点构成了3条边,他们所有可能构成的边为 C 4 2 = 4 × 3 2 = 6 C{^2_4}=\frac {4 \times 3} {2}=6 C42=24×3=6因此其聚类系数为 C i = 3 6 = 1 2 C_i=\frac {3}{6}= \frac {1} {2} Ci=63=21 |
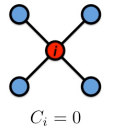 | 对于节点 i i i来说,邻居节点一共有4个,这4个邻居节点构成了0条边,他们所有可能构成的边为 C 4 2 = 4 × 3 2 = 6 C{^2_4}=\frac {4 \times 3} {2}=6 C42=24×3=6因此其聚类系数为 C i = 0 6 = 0 C_i=\frac {0}{6}= 0 Ci=60=0 |
1.4. 连通分量(Connected components) s s s
无向图G的极大连通子图称为G的连通分量( Connected Component)。任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。
如何找到一张图的联通分量?
- 随机选择一个节点作为起点,进行广度优先搜索;
- 将广度优先搜索经过的节点进行标记;
- 如果所有的节点都进行了标记,则该图是一个连通图;
- 如果存在未标记的节点,从未标记的节点中随机选择一个节点作为起点进行广度优先搜索;重复第2步和第4步,直至所有节点都标记完毕;最后得到的多个连通子图中对的极大连通子图就是该图的连通分量。
2. 一些真实网络案例的属性计算
2.1 MSN Messager网络
通过MSN一个月的对话活动构建。网络中有180M的用户(节点),1.3B的边(即连个用户之间至少发了一条信息)。我们可以看一下MSN网络的一些属性:
| 属性 | 结果 | 讨论 |
|---|---|---|
| 度分布(Degree distribution) | 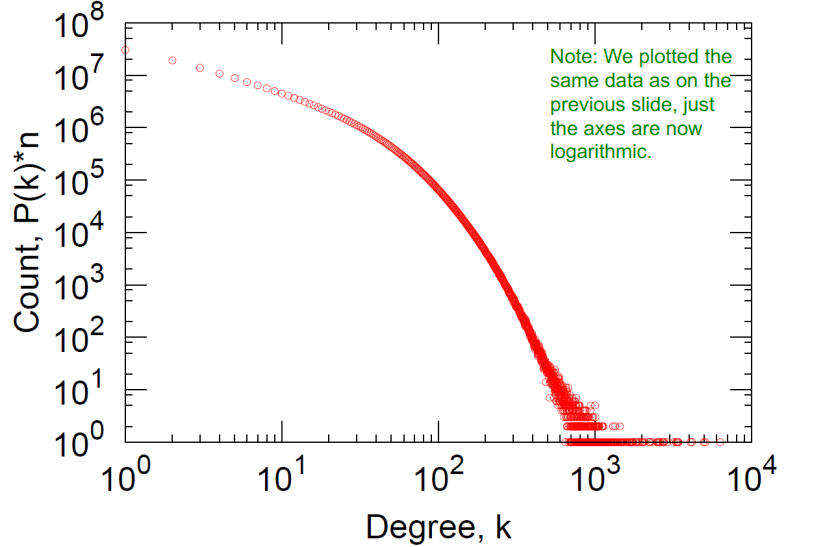 | 严重倾斜。 k ‾ = 14.4 \overline{k}=14.4 k=14.4。 |
| 聚类系数(Clustering coefficient) | 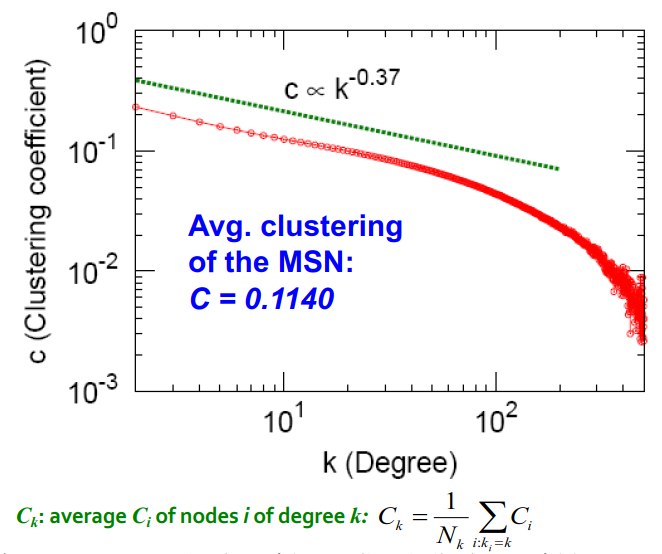 | C ‾ = 0.11 \overline{C}=0.11 C=0.11 |
| 连通分量(Connected components) | 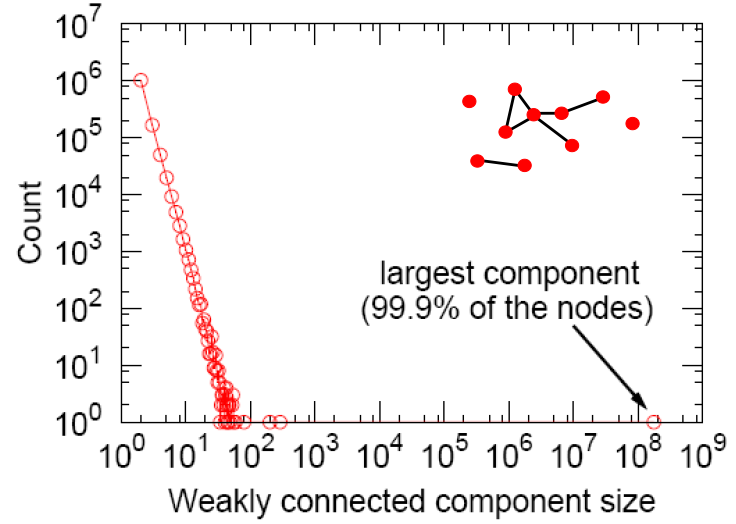 | 强连通,MSN网络的连通分量中包含了99%的节点。 |
| 路径长度(Path length) | 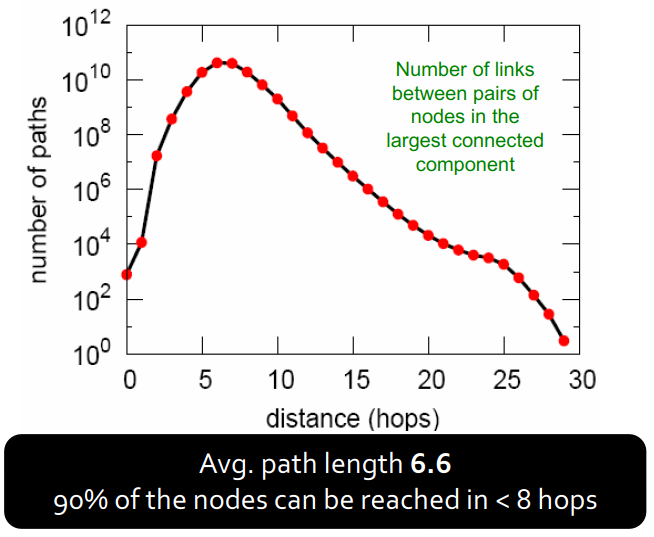 | 平均路径长度为6.6。从图中可以看出,超过 1 0 10 10^{10} 1010对节点之间的距离是6,可能这就是所谓的认识6个人,就认识了全世界吧hh。两个人之间最多通过30人就可以互相认识。 |
2.2 PPI网络(蛋白质相互作用的网络)
PPI网络中包含2018个结点(2018种蛋白质),2930条边。
| 属性 | 结果 | 讨论 |
|---|---|---|
| 度分布(Degree distribution) | 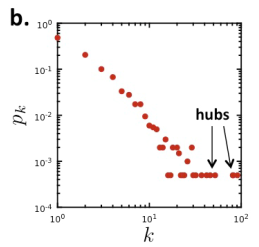 | 倾斜。 < k > = 2.9 <k>=2.9 <k>=2.9。 |
| 聚类系数(Clustering coefficient) | 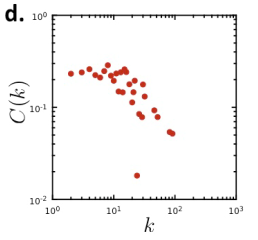 | C ‾ = 0.12 \overline{C}=0.12 C=0.12 |
| 连通分量(Connected components) | 有185个连通子图,其连通分量中包含1647个结点(81%的节点)。 | |
| 路径长度(Path length) | 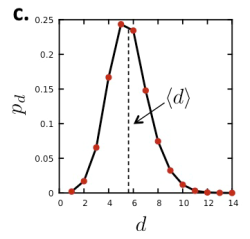 | 平均路径长度为5.8。 |
在计算了这些网络的参数之后,这些参数有哪些实质的意义呢?这两个网络的参数也——聚类参数和路径长度也很接近。为了获得这些参数的意义,需要一些图模型作为benchmark。
3. 最简单的图模型——ER Random Graph Model (ER随机图模型)
在数学中,随机图是指由随机过程产生的图。
在图论的数学理论部分中,ER模型(Erdős–Rényi model)可指代两个密切相关的随机图生成模型中的任意一个。这两个模型的名称来自于数学家Paul Erdős(保尔•厄多斯)和Alfréd Rényi(阿尔弗烈德•瑞利),他们在1959年首次提出了其中一个模型,而另一个模型则是Edgar Gilbert(埃德加•吉尔伯特)同时并且独立于Erdős和Rényi提出的。在Erdős和Rényi的模型中,节点集一定、连边数也一定的所有图是等可能的;在Gilbert的模型中,每个连边存在与否有着固定的概率,与其他连边无关。在概率方法中,这两种模型可用来证明满足各种性质的图的存在,也可为几乎所有图的性质提供严格的定义。
ER随机图模型有两种,一个是 G n p G_{np} Gnp图,给定 n n n个节点和节点之间生成边的概率 p p p;一个是 G n m G_{nm} Gnm图,给定 n n n个节点和 m m m条边,这 m m m条边随机在这 n n n个节点间生成。
3.1 G n p G_{np} Gnp图
在模型 G n p G_{np} Gnp中,随机连接节点构成一个图。图中每个连边彼此独立,连接的概率为 p p p。等价地,拥有 n n n个节点、 M M M个连边的所有图具有相同的概率。
需要注意的是,给定节点 n n n和概率 p p p,并不意味着生成唯一的图。下面是 n = 10 n=10 n=10和 p = 1 / 6 p=1/6 p=1/6时生成图的一些例子:

下面介绍 G n p G_{np} Gnp图的一些性质。
G n p G_{np} Gnp图的度分布(Degree distribution)
G n p G_{np} Gnp图的度分布是二项分布(binomial)。
P ( k ) = C n − 1 k p k ( 1 − p ) n − 1 − k P(k)=C{^k_{n-1}} p^k (1-p)^{n-1-k} P(k)=Cn−1kpk(1−p)n−1−k
对于某个节点来说,度为 k k k的概率为从剩下的 n − 1 n-1 n−1个点中选取 k k k个点,并与之相连的概率。
由二项分布的性质,可以得到:
k ‾ = p ( n − 1 ) \overline{k}=p(n-1) k=p(n−1)
σ 2 = p ( 1 − p ) ( n − 1 ) \sigma^2=p(1-p)(n-1) σ2=p(1−p)(n−1)
σ k ‾ = [ 1 − p p 1 n − 1 ] 1 2 ≈ 1 ( n − 1 ) 1 / 2 \frac {\sigma} {\overline{k}}= [\frac{1-p} {p} \, \frac {1}{n-1}]^{\frac{1}{2}} \approx \frac {1}{(n-1)^{1/2}} kσ=[p1−pn−11]21≈(n−1)1/21

根据大数定律,随着网络规模的增大,分布变得越来越窄(分布会越来越集中)——我们越来越确信一个节点的度在 k ‾ \overline{k} k附近。
G n p G_{np} Gnp图的聚类系数(Clustering coefficient)
G n p G_{np} Gnp图的聚类系数(Clustering coefficient)由公式 C i = = 2 e i k i ( k i − 1 ) C_i==\frac {2e_i}{k_i(k_i-1)} Ci==ki(ki−1)2ei得到。
我们首先得到 e i e_i ei的期望值
E [ e i ] = p k i ( k i − 1 ) 2 E[e_i]=p \frac {k_i(k_i-1)}{2} E[ei]=p2ki(ki−1)
这里 p p p为一对节点相连的概率; k i ( k i − 1 ) 2 \frac {k_i(k_i-1)}{2} 2ki(ki−1)表示节点 i i i的邻居节点集能产生的边的数量。则
E ( C i ) = 2 E [ e i ] k i ( k i − 1 ) = p = k ‾ n − 1 ≈ k ‾ n E(C_i)=\frac {2E[e_i]}{k_i(k_i-1)}=p=\frac {\overline{k}}{n-1} \approx \frac {\overline{k}}{n} E(Ci)=ki(ki−1)2E[ei]=p=n−1k≈nk
随机图的聚类系数通常都比较小。If we generate bigger and bigger graphs with fixed avg. degree k k k (that is we set p = k ⋅ 1 / n p=k \cdot 1/n p=k⋅1/n), then C decreases with the graph size n n n.
G n p G_{np} Gnp图的路径长度(Path length)
G n p G_{np} Gnp图的路径长度(Path length)通过扩展数(expansion)来衡量。

扩展数 α \alpha α的计算如图所示,它描述了图的任意节点集与剩余节点之间边的数量。对于图中节点 V V V的任意子集 S S S,从该子集中的节点指向其补集 V \ S V \backslash S V\S中的节点的边 # of edges leaving S ≥ α ⋅ min ( ∣ S ∣ , ∣ V \ S ∣ ) \text{ \# of edges leaving S} \geq \alpha \cdot \min (|S|,|V \backslash S|) # of edges leaving S≥α⋅min(∣S∣,∣V\S∣)。扩展数 α \alpha α通常也用来衡量图的鲁棒性(可扩展性)。
简单理解为:任取图中节点的一个子集,相对应的从子集中离开的(也就是和这些节点相关的)最小节点数目。
或者还可以理解为:为了让图中一些节点不具备连接性,需要cut掉图中至少多少条边?
(answer:需要至少cut掉 α ⋅ N \alpha \cdot N α⋅N条边)
——摘自:图机器学习 2.2-2.4 Properties of Networks, Random Graph
如果一个图有 n n n个节点,其扩展系数为 α \alpha α,对于所有的节点对的来说,路径长度为 O ( ( log n ) / α ) O((\log n)/\alpha) O((logn)/α)。
对于 G n p G_{np} Gnp图来说,存在一个常数 c c c,使得 log n > n p > c \log n > np > c logn>np>c, d i a m ( G n p ) = O ( ( log n ) / log ( n p ) ) diam(G_{np})=O((\log n)/\log (np)) diam(Gnp)=O((logn)/log(np))。 p p p衡量的是两个节点之间随机生成边的概率, p p p越大,遍历 G n p G_{np} Gnp图所需要的步数越小。
同时, G n p G_{np} Gnp图的可扩展性很好,所以通过广度优先搜索来遍历图中的所有节点相对比较容易:

其实我在看这一部分的时候理解起来比较费劲,而且在google上各种关键词搜索都没有搜索到讲的比较明确的资料。不过上面这张图还是画的比较明白的,可以结合图的广度优先生成树/森林来理解。
同时可以看到,在 p p p一定的情况下,随着节点数的增长, G n p G_{np} Gnp图的平均最短路径趋于某一个值。。

G n p G_{np} Gnp图的连通分量(Connected components)
p p p衡量的是两个节点之间随机生成边的概率, G n p G_{np} Gnp图的连通性也会随着 p p p而改变:

在 p = 1 / ( n − 1 ) p=1/(n-1) p=1/(n−1)时,度平均为1,出现最大连通子图,每个节点至少有一条期望边。

3.2 G n p G_{np} Gnp图与实际网络的比较
我们将MSN网络与 G n p G_{np} Gnp图模型进行比较:

随机图模型与真实网络的比较:

随机图模型存在的一些问题:

- 真实网络的度分布与随机图模型不同;
- 真实网络的最大连通子图并不是通过相变(phase transition)产生的。
- 由于没有局部结构——导致随机图模型的聚类系数过低。
更重要的一点,真实网络并不是随机图模型。那么,既然 G n p G_{np} Gnp图模型是错误的,我们了解和研究 G n p G_{np} Gnp图模型的性质有什么意义呢?

4. 小世界网络模型 The Small-world model
前面讲到,随机图模型其实不符合真实网络的分布。随机图模型正确模拟真实世界网络中的平均路径长度,但是低估了聚类系数。为了解决这个问题,我们引入第二个模型——小世界网络模型(The Small-world model)
小世界网络模型是一类具有较短的平均路径长度又具有较高的聚类系数的网络的总称。
我们怎样去构建一个小世界网络模型呢?可以先看下面这两张图:

Clustering implies edge “locality”
Randomness enables “shortcuts”
左边这张图保证了聚集性(比如在现实社会中,我的朋友的朋友就是我的朋友这种情况),但是这种时候图的直径就会比较大,就好比大家都认识,想要传递消息的时候不能直接打电话,得有无数人中间传话一样;右边这张图是随机图模型,图的直径比较小,两两之间能够直接沟通的渠道变多了,但是缺少聚集性的特点。
这里我们介绍WS小世界模型构造算法 [Watts-Strogatz ‘98] :
1、**从一个环状的规则网络开始:**网络含有 N N N个结点,每个节点向与它最临近的 K K K个节点连出 K K K条边,并满足 N > > K > > l n ( N ) > > 1 N>>K>>ln(N)>>1 N>>K>>ln(N)>>1。
2、随机化重连:以概率 p p p随机地重新连接网络中的每个边,即将边的一个端点保持不变,而另一个端点取为网络中随机选择的一个节点。其中规定,任意两个不同的节点之间至多只能有一条边,并且每一个节点都不能有边与自身相连。这样就会产生 p N K / 2 pNK/2 pNK/2条长程的边把一个节点和远处的结点联系起来。改变 p p p值可以实现从规则网络( p = 0 p=0 p=0)向随机网络( p = 1 p=1 p=1)转变。

小世界网络模型给我们描述真实的网络提供了一个比较贴切的模型:

5. Kronecker Graph Model——Generating large realistic graphs
我们怎样有效地构建超大的图呢?这里引入一个概念:自相似性(Self-similarity)——物体总是和自身的某些局部是相似的。Kronecker Graph Model就是通过递归来生成网络。其递归的方法是通过Kronecker乘积来实现的,Kronecker乘积就是生成自相似矩阵的一种方式。

Kronecker图就是通过一系列初始矩阵 K 1 K_1 K1与自身的Kronecker乘积来得到:
K 1 [ m ] = K m = K 1 ⊗ K 1 ⊗ ⋯ ⊗ K 1 ⏟ m times = K m − 1 ⊗ K 1 K{^{[m]}_1}=K_m=\underbrace{K_1 \otimes K_1 \otimes \cdots \otimes K_1}_{\text{m times}}=K_{m-1} \otimes K_1 K1[m]=Km=m times K1⊗K1⊗⋯⊗K1=Km−1⊗K1
Stochastic Kronecker Graph Model 随机Kronecker图模型
- 生成 N 1 × N 1 N_1 \times N_1 N1×N1的概率矩阵 Θ 1 \Theta_1 Θ1
- 递归计算第 k k k个Kronecker乘积 Θ k \Theta_k Θk
- Θ k \Theta_k Θk中的值 p u v p_{uv} puv表示节点 u u u和节点 v v v之间生成边的概率
- 按照这个概率产生实际的邻接矩阵,得到最后的大图模型

但是,这时候生成邻接矩阵的计算量回达到 N 2 N^2 N2次,速度会很慢。为了提高计算效率,我们引入drop操作——就是在 n = 2 m n=2^m n=2m个结点中递归生成边。
快速克罗内克图生成算法(Fast Kronecker Generator Algorithm)(用于生成有向图)
- 构建归一化概率矩阵 L u , v = Θ u , v / ( ∑ Θ 矩阵内的素有元素之和 ) L_{u,v}=\Theta_{u,v}/(\sum \Theta \text{矩阵内的素有元素之和}) Lu,v=Θu,v/(∑Θ矩阵内的素有元素之和)
- F o r i = 1 ⋯ m : For \, i=1 \cdots m: Fori=1⋯m:
- 令 x = 0 x=0 x=0, y = 0 y=0 y=0,
- 通过概率矩阵中的概率值随机选取一个元素 ( u , v ) (u,v) (u,v)
- 在 u , v u,v u,v所在的象限内计算一个求和值 X + = u ⋅ 2 m − i X+=u \cdot 2^{m-i} X+=u⋅2m−i, Y + = v ⋅ 2 m − i Y+=v \cdot 2^{m-i} Y+=v⋅2m−i - 在图 G G G中添加边 ( X , Y ) (X,Y) (X,Y)
这是真实网络和克罗内克图模型的比较:

这篇关于cs224w 图神经网络 学习笔记(二)Properties of Networks and Random Graph Models的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









