概率机器人2_C2 状态估计-贝叶斯滤波器

本文主要是介绍概率机器人2_C2 状态估计-贝叶斯滤波器，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Abbr:

TBD

牢记

重点

后验：posterior ，先验：prior
概率密度函数： PDF
一维正态分布表示：
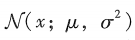
离散时间：本书中的时间将是离散的, t1,t2,t3,... tn
状态用 x 表示，尽管 x 所包含的具体变量取决于上下文。时间 t的状态表示为 xt 。
在时间 t 的测量数据表示为 zt
控制数据用 ut表示
pose : 6自由度表示 : （x,y,z）坐标和对应的三个旋转角（roll,pitch,yaw）--一阶就是得到速度变化率，只在平面上运动的话，就缩减为（x,y,0）,(0,0,yaw=heading angle) 3个自由度。
系统状态等于某一个绝对值（真值）的概率。用bel (xt)表示
运动学状态 =(kinematic state)
地标：环境物体的位置都是静态的。本书将物体假设为地标 (landmarks) 形式
状态 xt,是随机地，由状态 xt-1 产生的。因此，指定生成 xt的概率分布是有意义的。表示为： 。如果状态 x 是完整的，那么它是所有以前时刻发生的所有状态的充分总结

本节是全书的理论基石。

Recursive State Estimation 递归状态估计

核心：就是由传感器数据来进行“状态估计”

状态方程中的状态变量通常不能被传感器准确，直接测得。---无法只通过一次测量确定位姿（同一个场景中，如果有相同的门，没法确定是哪一个！）。必须长时间整合数据以确定它的位姿。而且还混杂了噪声。因此用概率置信度来估计状态变量。比如定位问题，机器人自己在哪儿？--98%的概率处于坐标（x,y）处。

1. 基本概念：

随机变量：传感器测量、控制、机器人的状态及其环境

概率推理: 由其他随机变量和所观测数据推导随机变量的相关定律的过程
Probability Density Function PDF : p(x)

概率密度函数：的积分总为1，

一维正态分布PDF:

多维正态分布的PDF：

协方差矩阵：

本书假设：连续空间，随机变量的取值连续, 都存在概率密度函数

联合分布-joint distribution ，独立的事件(随机变量取值为x,y --传感器测量值为z1,z2 ...）的联合分布就是p(z1,z2...)=p(z1)p(z2)...

条件概率：p(zt| zt-1,zt-2,...) 传感器历史测量值zt-1,zt-2 .. 发生的条件下，测量值为zt的概率。Zt 是真值。

一般表达式--p(x,y)/p(y)= p(x|y) ,如果x,y 独立，则，p(x).p(y)/ p(y）= p(x) = p (x|y)

Y 不会有任何关于 X 值的信息。如果对 X 感兴趣则知道 Y 值没有任何帮助

全概率公式：

事件Y在y 取值空间内，能得到事件(结果）X=x值得可能性，先验过程

贝叶斯公式：表达了条件概率和 "逆"条件概率的关系

条件y=全概率-对应结果，x某一个原因， x' 表示所有的原因

已知：全概率，已知条件概率，求出逆条件概率，就直接运用公式。

x--对应原因(推测的状态变量值)，y--结果（表示传感器的测量值zt-1,zt-2,...），已知结果，求原因，后验估计

注：下图中，分子上的x，或等式坐标的x的取值是某一个值，分母下面x'表示x的全部可能取值。这样才能利用全概率公式，求出p（y）

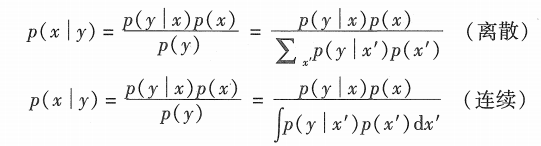
概率 p(ylx) 经常被称为生成模型 (generative model) , 因为在一定的抽象层面上，它表示状态变量 X 如何引起了检测数据

归一化的贝叶斯公式：

注： Vx-- 某一个任意x值，下面求和公式，x-x全部可能取值，为了得到全概率。

因此：贝叶斯，就是对应，一个条件下的xx事件的概率，比上全部条件下的xx事件的概率（全概率）== xx事件下，这一个条件发生的概率。

中文page 36

条件独立：

咋一看，状态 x, 的出现可能是以所有过去的状态xt-1、测量zt和控制ut为条件的。表示成： xt-1 和ut 可以表示xt的完整状态空间，和zt无关和历史的控制量，状态量也无关，所以利用条件独立，得到

同理对于测量来说：只和当前的状态有关。

由上面的定义获得 2个概率定义--

测量概率： xt 表示当前状态，zt是测量值。测量的结果由环境状态x产生。测量不准确有噪声，所以用概率的形式表示测到这个zt的真值的概率。这就是测量概率法则

状态转移概率state transition probability：

马尔可夫链 (Markov chain) ：未来xt+1...可以是随机的，但是没有先于xt, 的历史状态变化可以影响未来状态的随机变化，除非这种依赖通过状态 xt, 起作用。满足这些条件的暂态过程通常称为马尔可夫链 (Markov chain) 。历史状态：xt-1,xt-2,xt-3.... 当前状态xt, 未来的状态xt+1,xt+2... （结合了上面2个概率-构成马尔科夫）

状态转移概率和测量概率一起描述机器人及其环境组成的动态随机系统。时刻t 的状态随机地依赖 t -1 时刻的状态和控制 ut, 。测量 zt, 随机地依赖时刻 t 的状态。

隐马尔可夫模型=动态贝叶斯网络：下图时间生成模型也称为隐马尔可夫模型 (Hidden Markov Model , HMM) 或者动态贝叶斯网络 (Dynamic Bayes Network, DBN)

置信分布 ≈ 条件概率

我们无法直接测量系统的状态（位姿 -6自由度）。传感器的测量也不能直接测量获得位姿，同时含有噪声干扰的。

我们只能从历史测量数据中推断出 系统的状态（可能概率--置信度）。

因此有必要通过置信度来表达，系统状态等于某一个绝对值（真值）的概率。bel (xt)表示。

已知历史测量值（条件下），后验概率（条件概率）表示为：

考虑了， t 时的测量值Zt, 所有的历史测量和历史控制。

(注意比较前面的公式，想一想，~~如果xn 不能准确获得，只能通过测量和控制量来预测，就能理解了。~~ 这里和下面贝叶斯滤波器，冲突，感觉公式改成 bel(xt）=p(xt| xt-1,ut) 更make sense.）

概率滤波器-框架：

如果只是用t-1之前的测量和，历史控制，获得的bet(xt)为预测阶段：（xt还未发生，还未测量），表示

，（注意算法时间的话，应该用积分（算法求和）来表示1：t的所有历史信息）测得zt之后，，结合预测的，进行修正，来更新预测( 测量更新阶段）：

注：priro --就是贝叶斯公式中右边，条件的每一个取值的概率。）分布情况，只有已知了。

贝叶斯滤波器：(中文page 38)

利用上面的公式预测和更新公式。

预测：，bel(xt-1)，表示t-1时刻的置信度，前面的是状态转移概率。相乘表示同时发生的可能性。积分，表示历史信息的叠加.1到 t-1 时刻

更新；，p(xt|zt)= ?利用贝叶斯公式，获得。

初始化：，bel(x0) =xxx（x0,所有取值空间对应的概率，-先验）, u0...t （转移概率分布）已知， z0...t （测量概率分布）已知。

这样可以预测下个时刻的bel(xt). 后验估计。（注意积分项，算法中实现就是一个累加的过程。）

这样系统就迭代循环起来了。推导过程参考：<中文page41>

注：注意xt-1 的下标。

算法：

TBC: 如何初始化定义这三个概率分布。chapter 5--转移概率， chapter 6-测量概率，先验概率 bel(x0) chapter 3&4

举例：

已知：

机器人可以测量（z1...zn, 取值空间为：开，关，对应测量概率分布p（zt|xt）--传感器概率模型），动作：（u1...ut,取值空间为：开门、关门，对结果的影响，对应状态转移概率，p(xt|xt-1,ut), 系统x状态：开、关，对应的先验概率分布情况

这样可以估计任意时刻的置信度： bel(xt| zt,ut) = ??

总结：

假设世界是马尔可夫的，也就是状态是完整的，贝叶斯滤波算法以到时间 t 的测量和控制数据为条件来计算状态 x。是一种后验估计。
2个概率法则：状态转移概率，测量概率； 贝叶斯估计（置信度bel(x)）依赖有关测量、状态转移概率和初始置信度bel(x0)的假定，概率模型建模的过程肯定需要数学近似。近似过程（概率建模过程）需要考虑：时间复杂度/效率，精度，算法实现容易程度。
贝叶斯滤波不是一个实际的算法，不能用数字计算机实现。基于贝叶斯滤波框架有很多经典的算法，比如卡尔曼滤波、粒子滤波 etc...