本文主要是介绍304.二维区域和检索 - 矩阵不可变│leetcode,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) 。3 0 1 4 2
5 6 3 2 1
1 ┏2━━0━━1┓ 5
4 ┃1 0 1┃ 7
1 ┗0━━3━━0┛ 5上图子矩阵(框中)左上角 (row1, col1) = (2, 1) ,右下角(row2, col2) = (4, 3),该子矩形内元素的总和为 8。示例:给定 matrix = [[3, 0, 1, 4, 2],[5, 6, 3, 2, 1],[1, 2, 0, 1, 5],[4, 1, 0, 1, 7],[1, 0, 3, 0, 5]
]sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12提示:
你可以假设矩阵不可变。
会多次调用 sumRegion 方法。
你可以假设 row1 ≤ row2 且 col1 ≤ col2 。
以上是题目给出的所有内容,我们可以先用最简单粗暴的方法写出一个解题方法。最简单粗暴的方法当然是循环遍历啦。
根据给出的子矩阵的左上角坐标和右下角坐标,循环遍历子矩阵中所有的点并相加,就是最终结果。上代码:
class NumMatrix:def __init__(self, matrix: list[list[int]]):self.matrix = matrixdef sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:sum_region = 0for row in range(row1, row2 + 1): # 循环列(|)for col in range(col1, col2 + 1): # 循环行(一)sum_region += self.matrix[row][col]return sum_region
这种方法在时间复杂度和空间复杂度上都是 O(m*n),甚至通过了提交,这道题完结,撒花。
但是这道题不能就此罢休,因为上面的解法虽然可以通过测试,但是使用的方式不是这道题想要考察的方式。 在题目的提示中,提到了会多次调用 sumRegion() 方法。 并且在给出的初始代码中也提示到在测试时会先实例化对象,然后再执行方法。
根据以上的种种提示,可以知道这道题是想让我们在实例化对象时就将二维数组进行预处理,然后在调用 sumRegion() 方法时可以更加高效的得到结果。
那么,热身结束,正文开始:
想一想,怎样才能在只给出子矩阵的左上角和右下角坐标的情况下最快得到子矩阵所有点之和呢?
我自己最先想到的方法是计算出矩阵中当前坐标与它同一行内之前所有坐标之和,这样在计算子矩阵坐标之和时,每行的坐标之和就可以通过简单的计算得出,而不是使用遍历累加。
如下图所示,新矩阵的每个坐标上的值都是与之同一行之前坐标的总和,那么在计算一行的子区间之和时,就可以通过右边界坐标(图中蓝底红字)的值减去左边界坐标再左移一位(图中橙底红字)的值算出。
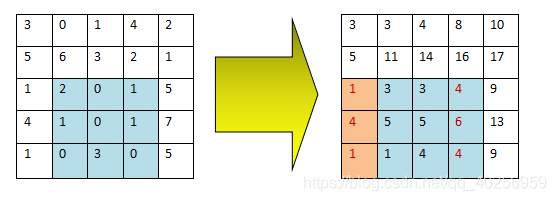
计算子矩阵的坐标值之和,就可以遍历每行的值,然后累计。这种方式计算的时间复杂度降到了 O(m)。代码如下:
class NumMatrix:def __init__(self, matrix: list[list[int]]):self.matrix, self.colSum = matrix, []for i in range(0, len(self.matrix)):self.colSum.append([])col_sum = 0for col in self.matrix[i]:col_sum += colself.colSum[i].append(col_sum)def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:sum_region = 0# 只需要循环列(|)for row in range(row1, row2 + 1):# 每行右坐标的值减去左坐标再左移一位的坐标的值# 因为左移后索引可能为 -1 所以要增加一个判断sum_region += self.colSum[row][col2] - (self.colSum[row][col1 - 1] if col1 != 0 else 0)return sum_region
运算效率相比最初的方法已经大大提高了,但是这足够吗? 假如 sumRegion() 方法需要执行很多次,那么总的时间复杂度又达到了 O(m*n),最初的方法的时间复杂度就是 O(m*n*k)。那么,还有没有效率更高的方法呢?
答案是有,既然可以在每行的坐标中统计行 0 点坐标到当前坐标的累加值,那就可以提前计算出 (0, 0) 坐标到当前坐标的子矩阵累加值。计算子矩阵坐标值之和就只需要简单计算一次即可。
假设求左上角坐标 (A, B),右下角坐标为 (C, D) 的子矩阵坐标值之和。现在 (C, D) 坐标的值已经是 (0, 0) 到 (C, D) 坐标值之和了,那么这个值减去多余位置的值就是需要的答案了。那么减去一个 (0, 0) 到子矩阵右上角的坐标 (A - 1, D) 子矩阵(黄色部分+红色部分),减去一个 (0, 0) 到子矩阵左下角的坐标 (C, B - 1) 子矩阵(紫色部分+红色部分)。这时发现两次减操作中有重复区域(红色部分),那么还需要重新加上这部分,(0, 0) 到 子矩阵左上角的坐标 (A, B) 子矩阵(红色部分)。

计算公式为(坐标内的值是 (0, 0) 到当前点的子矩阵坐标值总和, 标记为 S):
子矩阵坐标值之和 = S(C, D) - S(A - 1, D) - S(C, B - 1) + S(A - 1, B - 1)
计算子矩阵坐标值之和问题解决了,但是有个前置问题没有解决,怎样得到每个坐标相对于 (0, 0) 坐标之间的子矩阵坐标值之和。
总不能每个坐标点都进行一次循环列加循环行的二维遍历吧,这样做效率太低了。其实可以理解为子矩阵坐标值之和的反推。假设要得到 (A, B) 坐标相对与 (0, 0) 坐标之间的子矩阵坐标值之和,那么可以将 (0, 0) 到 (A - 1, B) 子矩阵(紫色部分+红色部分)与 (0, 0) 到 (A, B - 1) 子矩阵(黄色部分+红色部分)相加,这时 (A - 1, B - 1) 子矩阵是被计算了两次,将这一子矩阵的值减去,最后再加上 (A, B) 的坐标值就是 (A, B) 坐标相对于 (0, 0) 坐标之间的子矩阵坐标值之和。

计算公式为(坐标内的值是 (0, 0) 到当前点的子矩阵坐标值总和, 标记为 S):
坐标相对原点的子矩阵坐标值之和 = (A, B) + S(A - 1, B) + S(A, B - 1) - S(A - 1, B - 1)
这时初始化计算所有坐标与原点的子矩阵坐标值之和的时间复杂度为 O(n*m),sumRegion() 方法的时间复杂度为 O(1),即使执行 N 此,总时间复杂度也是 O(N). 代码如下:
class NumMatrix:def __init__(self, matrix: list[list[int]]):self.matrix, self.preSum = matrix, []for row in range(0, len(self.matrix)):self.preSum.append([])for col in range(0, len(self.matrix[row])):# 区域A: (0, 0)->(A - 1, B) 区域B: (0, 0)->(A, B - 1) 重复区域: (0, 0)->(A - 1, B - 1)# 有对索引值减操作, 要主要索引边界区域A = self.preSum[row - 1][col] if row > 0 else 0区域B = self.preSum[row][col - 1] if col > 0 else 0重复区域 = self.preSum[row - 1][col - 1] if (row > 0 and col > 0) else 0self.preSum[row].append(self.matrix[row][col] + 区域A + 区域B - 重复区域)def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:区域A = self.preSum[row1 - 1][col2] if row1 > 0 else 0区域B = self.preSum[row2][col1 - 1] if col1 > 0 else 0重复区域 = self.preSum[row1 - 1][col1 - 1] if (row1 > 0 and col1 > 0) else 0return self.preSum[row2][col2] - 区域A - 区域B + 重复区域
总结,经过一步步的优化,计算效率越来越高。我个人很喜欢这样的风格,先做出一个最简单粗暴但是效率不高的方法,然后再一步步优化。最后放出这三种方法的用时情况。

公众号 : 「python杂货铺」,专注于 python 语言及其相关知识。发掘更多原创文章,期待您的关注。关注并回复「python」获取 python 相关资料。

这篇关于304.二维区域和检索 - 矩阵不可变│leetcode的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




