本文主要是介绍麻省理工公开课算法导论(二):Insertion Sort and Merge Sort,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- Introduction
- Insertion Sort and Merge Sort
- Why Sorting?
- Insertion Sort
- Binary Insertion Sort
- Merge Sort
- Code Implements
- Summary
Introduction
本篇来自于笔者学习MIT的公开课算法导论的学习笔记,仅仅是我个人接受课程教育后,进行的学习笔记,可能理解并不到位,仅供参考。
课程视频地址:
Lecture 3: Insertion Sort and Merge Sort
Insertion Sort and Merge Sort
Why Sorting?
首先让我们思考一个问题,为什么我们需要排序?
在日常生活中的很多场景,例如管理MP3的歌曲列表、维护手机通讯录等等,针对这些场景,排序可以将问题变得更加的简单。
Insertion Sort
接下来我们介绍一种排序算法,叫做插入排序(Insertion Sort)。
假定给定有序数组A[1…j-1],我们希望将元素A[j]插入有序数组数组中,如下图:

当然,这是非常理想的情况,我们只需要遍历数组,通过前后元素大小比较,找到A[j]应该插入到的位置,在该种情况下,时间复杂度为O(n)。
但是情况往往不可能会这么好,假定给定数组A[1…j-1],其中元素是乱序,我们希望将元素A[j]插入有序数组数组中,如下图:

最简单的思路,我们随机选定一个位置的元素,然后进行两两比较,比较前后元素的大小,如果前面元素大于自身,那么将前面的元素与自身交换,以此类推:









这就是最基本的插入排序算法,但是我们可以看出来,这种方式是非常的“看运气”,时间复杂度取决于原有的数组的元素排列顺序,时间复杂度非常不稳定,最差时间复杂度为T = O( n 2 n ^ 2 n2) + O( n 2 n ^ 2 n2),需要 n 2 n ^ 2 n2次比较和 n 2 n ^ 2 n2次交换。
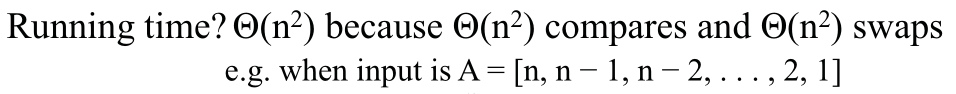
OK,这显然并不是一个非常棒的解决方案,那么是否可以对其进行优化呢,答案是可以的。
Binary Insertion Sort
二分法查找是一个非常经典的查找算法,我们在上一章中也介绍过二分法查找,该种算法的时间复杂度为O( log 2 ( n ) \log_2(n) log2(n)),我们可以尝试将二分法查找引入插入排序算法,即二分插入排序。
结合上面的步骤,插入排序算法中需要将被插入元素与其他元素进行比较,需要 n 2 n ^ 2 n2次比较,我们可以将该步操作改为二分法,即需要 log 2 ( n ) \log_2(n) log2(n)次比较, n 2 n ^ 2 n2次交换。
因此二分查找算法的时间复杂度为T = O( log 2 ( n ) \log_2(n) log2(n)) + O( n 2 n ^ 2 n2),需要 log 2 ( n ) \log_2(n) log2(n)次比较和 n 2 n ^ 2 n2次交换。

引入二分法后,我们取得了一定的性能提升,但是这仍不是一个特别出色性能的算法,我们希望寻找一个O( log 2 ( n ) \log_2(n) log2(n))的排序算法来解决排序问题。
Merge Sort
我们延续上面的思路,引入二分法查找是一个正确的选择,那么在此之上,我们再进一步,同时加入递归方法,这就是归并排序(Merge Sort)。

归并排序思想如下:
给定数组A[1…n],那么:
1、如果n = 1,结束;
2、否则,以数组中点为界分割成两个数组,递归排序A[1…n/2]与A[n/2 + 1…n];
3、合并两个排序好的数组。

排序示意图如下:

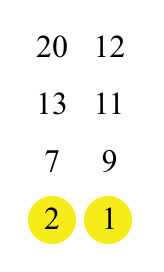
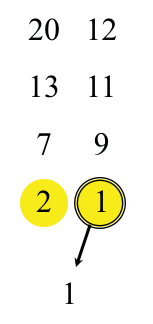
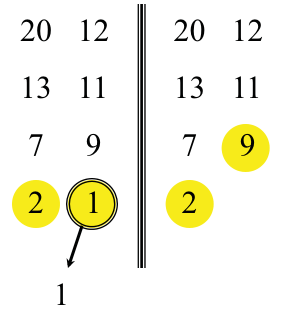
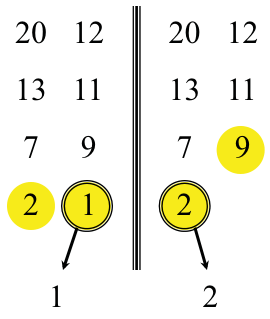









上图完整展示了整个排序的过程,通过该种方式,可以看出性能会高于插入排序算法,时间复杂度为:
T(n) = C1 + 2T(n/2) + O(n) + Cn 其中C>0 C为常数。
时间复杂度为O(n log 2 ( n ) \log_2(n) log2(n))
Code Implements
这里给出Java版本的代码实现参考:
public class MergeSort {/*** Merges two subarrays of arr[].* First subarray is arr[l..m]* Second subarray is arr[m+1..r]* @param arr* @param l* @param m* @param r*/private void merge(int arr[], int l, int m, int r) {// Find sizes of two subarrays to be mergedint n1 = m - l + 1;int n2 = r - m;/* Create temp arrays */int L[] = new int[n1];int R[] = new int[n2];/*Copy data to temp arrays*/for (int i = 0; i < n1; ++i) {L[i] = arr[l + i];}for (int j = 0; j < n2; ++j) {R[j] = arr[m + 1 + j];}/* Merge the temp arrays */// Initial indexes of first and second subarraysint i = 0, j = 0;// Initial index of merged subarry arrayint k = l;while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}/* Copy remaining elements of L[] if any */while (i < n1) {arr[k] = L[i];i++;k++;}/* Copy remaining elements of R[] if any */while (j < n2) {arr[k] = R[j];j++;k++;}}/*** Main function that sorts arr[l..r] using* merge()** @param arr* @param l* @param r*/private void sort(int arr[], int l, int r) {if (l < r) {// Find the middle pointint m = (l + r) / 2;// Sort first and second halvessort(arr, l, m);sort(arr, m + 1, r);// Merge the sorted halvesmerge(arr, l, m, r);}}/*** A utility function to print array of size n** @param arr*/private static void printArray(int[] arr) {int n = arr.length;for (int i = 0; i < n; ++i) {System.out.print(arr[i] + " ");}System.out.println();}/*** Driver method** @param args*/public static void main(String args[]) {int[] arr = {12, 11, 13, 5, 6, 7};System.out.println("Given Array");printArray(arr);MergeSort ob = new MergeSort();ob.sort(arr, 0, arr.length - 1);System.out.println("\nSorted array");printArray(arr);}
}
Summary
本篇我们介绍了两种排序算法——插入排序与归并排序,可以看到,两种排序的核心思想都依赖于二分法查找,对比一下两种算法的性能:
| Python | C | |
|---|---|---|
| 插入排序 | 0.2 n 2 n^2 n2 | 0.1 n 2 n^2 n2 |
| 归并排序 | 2.2n log 2 ( n ) \log_2(n) log2(n) |
当n>4000时,归并排序的性能会远远大于插入排序的性能,因此也是给我们一定的启示,当选择算法时,尽可能的要去选择时间复杂度为log函数的算法。
更多精彩文章, 请关注我的个人公众号:老宣说
让我们一起共同学习成长!
感谢您的支持!

这篇关于麻省理工公开课算法导论(二):Insertion Sort and Merge Sort的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








