cesium加载水域，一、第一种csv方法 1、获取水域csv坐标2、python水域坐标csv转换成数组 3、加载进cesium 二、第二种kml方法 1、画线2、另存为kml3、加载进cesium

本文主要是介绍cesium加载水域，一、第一种csv方法 1、获取水域csv坐标2、python水域坐标csv转换成数组 3、加载进cesium 二、第二种kml方法 1、画线2、另存为kml3、加载进cesium，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1、水域坐标下载（软件图形地球）

（1）下载图新地球，打开图新地图，选择绘制线，然后描绘你需要的水域

（2）描绘成功后选择底部的选中对象，在绘制好的线处双击左键，会出现导出坐标的选择表单

（3）

①导出为csv

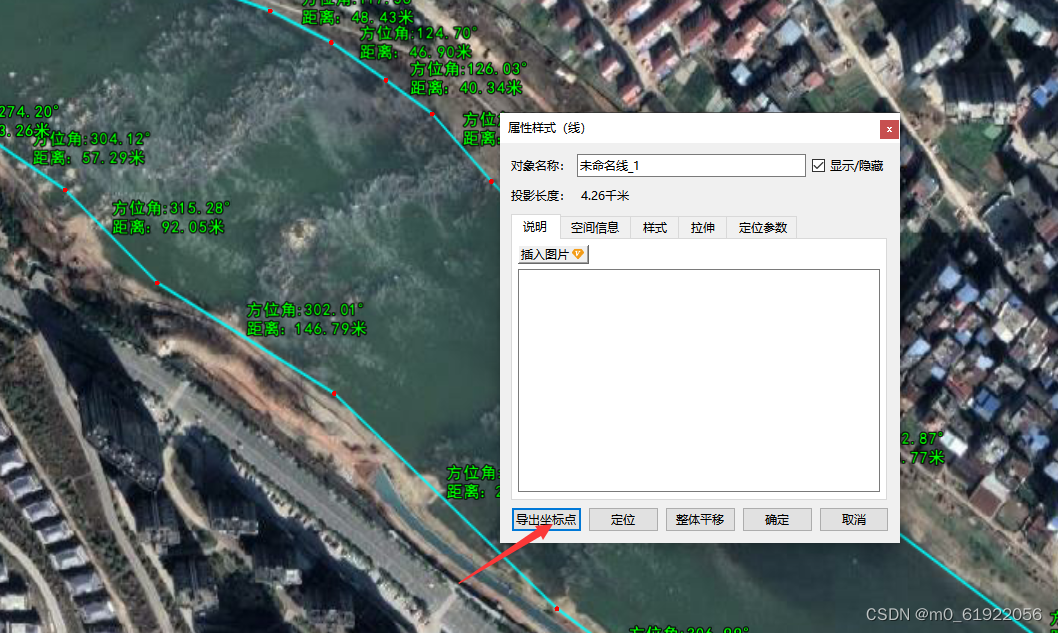
②导出为kml

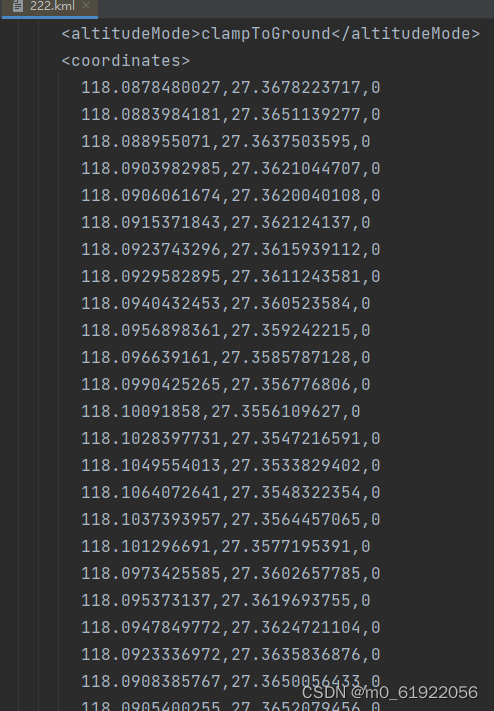
2、利用python将csv转换为数组（如果导出为kml，则这步不用）

csv部分数据，删除第一行，还有z值

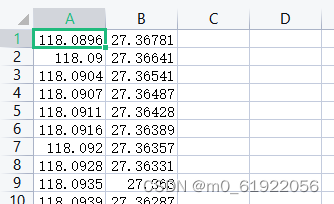
python代码运行

import csvwith open("D:\ditufabu\mm.csv") as f:                #读取文件reader = csv.reader(f)results = []results1 = []for row in reader: #读取csv的行数据results.append(row[0])results.append(row[1])print(results)for item in results:item1 = float(item)results1.append(item1)print(results1)

输出结果为数组，将数组放在箭头处。

3、加载进cesium

shuiyu.png要下载到你自己的项目里

cesium加载，该函数传入cesium的viewer实体

export function jiazaiShuiYu(_viewer){var Shuiyu_Polygon = _viewer.scene.primitives.add(new Cesium.Primitive({geometryInstances : new Cesium.GeometryInstance({geometry : new Cesium.PolygonGeometry({polygonHierarchy : new Cesium.PolygonHierarchy(Cesium.Cartesian3.fromDegreesArray([118.087848, 27.36782237, 118.0883984, 27.36511393, 118.0889551, 27.36375036, 118.0903983, 27.36210447, 118.0906062, 27.36200401, 118.0915372, 27.36212414, 118.0923743, 27.36159391, 118.0929583, 27.36112436, 118.0940432, 27.36052358, 118.0956898, 27.35924222, 118.0966392, 27.35857871, 118.0990425, 27.35677681, 118.1009186, 27.35561096, 118.1028398, 27.35472166, 118.1049554, 27.35338294, 118.1064073, 27.35483224, 118.1037394, 27.35644571, 118.1012967, 27.35771954, 118.0973426, 27.36026578, 118.0953731, 27.36196938, 118.094785, 27.36247211, 118.0923337, 27.36358369, 118.0908386, 27.36500564, 118.09054, 27.36520795, 118.0904824, 27.36491148, 118.0905778, 27.36432773, 118.0901108, 27.36491176, 118.0896663, 27.36613381, 118.0894511, 27.36757821, 118.0894797, 27.3679435, 118.0878358, 27.36784121, 118.0878529, 27.36784342])),vertexFormat : Cesium.EllipsoidSurfaceAppearance.VERTEX_FORMAT})}),appearance : new Cesium.EllipsoidSurfaceAppearance({aboveGround : true}),show : true}));Shuiyu_Polygon.appearance.material = new Cesium.Material({fabric : {type : 'Water',uniforms : {baseWaterColor: new Cesium.Color(64 / 255.0, 157 / 255.0, 253 / 255.0, 0.5),normalMap:'../../static/shuiyu.png',frequency: 10000.0,animationSpeed: 0.01,amplitude: 50}}});}