第二种专题
iNOC产品部-杨辉三角的变形(第二种方法也可以通过,测试数据太弱,n10000就会爆的)
// iNOC产品部-杨辉三角的变形(第二种方法也可以通过,测试数据太弱,n>10000就会爆的) #include<bits/stdc++.h>using namespace std;int F(int n,int k){if(k==1||k==2*n-1)return 1;if(k<1||k>2*n-1)return 0;return F(n-1,k)+F(n-1,k-1)+F(n-1
去除appcompat_v7(第二种方法的补充)
当我们创建新的Android项目移除 create Activity前的选项框,通过这样做,eclipse将不会自动引用这个库项目“appcompat_v7”。然后你可以手动地创建主活动。但是如果你有fragment和actionbar这些控件时注意一定要引用。 之前的方式请 点击这里 !!!
创建按钮的第二种方法
可以设置两个参数,按钮的内容和父对象 QPushButton * button2 =new QPushButton("第二个按钮",this); 区别: 方式1:窗口默认大小,按钮显示在左上角 方式2:窗口是根据按钮的大小来创建的 (所以需要重置窗口的大小) this->resize(600,400); #include "widget.h"#include "ui_wi
第13节 第二种shellcode编写实战(2)
我最近在做一个关于shellcode入门和开发的专题课👩🏻💻,主要面向对网络安全技术感兴趣的小伙伴。这是视频版内容对应的文字版材料,内容里面的每一个环境我都亲自测试实操过的记录,有需要的小伙伴可以参考🫡 我的个人主页:https://imbyter.com 一、C语言方式编写shellcode 在第二种shellcode编写实战(1)的基础上,新增加一个CAPI类,将所有用到的
c++中类模板中的函数第二种情形:所有函数都在类的外部,但是都在一个cpp文件中
针对于所有的函数都在类的外部,但是都在一个cpp文件中的这种情形,只有友元函数的存在是比较特殊和难处理的。 (1) 类中只有成员函数的情况 代码如下,注意代码的书写规则: #include <iostream>using namespace std;template <typename T>class Complex{public:Complex(
蓝桥杯之二阶魔方旋转(第二种方法)
魔方可以对它的6个面自由旋转。 我们来操作一个2阶魔方(如图1所示) 为了描述方便,我们为它建立了坐标系。 各个面的初始状态如下: x轴正向:绿 x轴反向:蓝 y轴正向:红 y轴反向:橙 z轴正向:白 z轴反向:黄 假设我们规定,只能对该魔方进行3种操作。分别标记为: x 表示在x轴正向做顺时针旋转 y 表示在y轴正向做顺时针旋转 z 表示在z轴正向做顺时针旋转 基本旋
webpack学习—— webpack-dev-server(3)配置命令的第二种方式
第一种方式是直接在描述文件package.json 里配置 第二种方式是在 webpack.config.js 文件里声明
Linux环境下的Docker的三种常用方式安装(强烈推荐第二种安装方式)推荐Portainer GUI管理工具
Docker 是一个开源的应用容器引擎,基于 Go 语言 并遵从Apache2.0协议开源。 Docker 可以让开发者打包他们的应用以及依赖包到一个轻量级、可移植的容器中,然后发布到任何流行的 Linux 机器上,也可以实现虚拟化。 容器是完全使用沙箱机制,相互之间不会有任何接口(类似 iPhone 的 app),更重要的是容器性能开销极低。 Docker的应用场景:Web 应用的自动化
cesium加载水域,一、第一种csv方法 1、获取水域csv坐标2、python水域坐标csv转换成数组 3、加载进cesium 二、第二种kml方法 1、画线2、另存为kml3、加载进cesium
1、水域坐标下载(软件图形地球) (1)下载图新地球,打开图新地图,选择绘制线,然后描绘你需要的水域 (2)描绘成功后 选择底部的选中对象,在绘制好的线处双击左键,会出现导出坐标的选择表单 (3) ①导出为csv ②导出为kml 2、利用python将csv转换为数组(如果导出为kml,则这步不用) csv部分数据,删除第一行,还有z值 python代码
[Java] Thread 创建线程的第二种方法
public class Thread4{ public static void main(String[] args){ //利用多态 Thread t = new RunnableTest3(); t.start(); } } //用继承Thread父类的方法来定义 class RunnableTest3 extends Thre
html获取网络数据,列表展示 第二种
html获取网络数据,列表展示 第二种 js遍历json数组中的json对象 image.png || '-' 判断数据是否为空,为空就显示 - <!DOCTYPE html><html><head><meta charset="utf-8"><title>网页列表</title><script type="text/javascript">// https://api.t
MySQL 连接出现 Authentication plugin ‘caching_sha2_password的处理方法(使用第二种)
出现这个原因是mysql8 之前的版本中加密规则是mysql_native_password,而在mysql8之后,加密规则是caching_sha2_password, 解决问题方法有两种,一种是升级navicat驱动,一种是把mysql用户登录密码加密规则还原成mysql_native_password. 1. 升级MySQL版本 较早的MySQL版本可能不支持caching_sha2_
MySQL 连接出现 Authentication plugin ‘caching_sha2_password的处理方法(使用第二种)
出现这个原因是mysql8 之前的版本中加密规则是mysql_native_password,而在mysql8之后,加密规则是caching_sha2_password, 解决问题方法有两种,一种是升级navicat驱动,一种是把mysql用户登录密码加密规则还原成mysql_native_password. 1. 升级MySQL版本 较早的MySQL版本可能不支持caching_sha2_
Python——调试 (第二种debug)
#coding=utf-8import pdbdef combine(s1,s2):s3 = s1 + s2 + s1s3 = '"' + s3 +'"'return s3a = "aaa"pdb.set_trace()b = "bbb"c = "ccc"final = combine(a,b)print(final)# 《1 显示代码》# l---->能够显示当前调试过程中的代码,
(二)Spring WeFlux响应式编程第二种整合方案|道法术器
特注意: Spring Boot 的版本大于等于 2.3.0,在此版本之后才开始支持 MYSQL 的响应式驱动 在执行程序时: 通常为了提供性能,处理器和编译器常常会对指令进行重排序。 从排序分为编译器重排序和处理器重排序两种 : (1)编译器重排序: 编译器保证不改变单线程执行结构的前提下,可以调整多线程语句执行顺序;
Android 13.0 首次开机默认授予app运行时权限(去掉运行时授权弹窗)第二种方法
1.概述 在13.0的系统产品开发中,在6.0以后对于权限的申请,都需要动态申请,所以会在系统首次启动后,在app的首次运行时,会弹出授权窗口,会让用户手动授予app运行时权限,在由于系统产品开发需要要求默认授予app运行时权限,不需要用户默认授予运行时弹窗,所以需要在首次开机默认授予所有app运行时权限 2.首次开机默认授予app运行时权限(去掉运行时授权弹窗)第二种方法的解决方案的核心
计算重叠积分的第二种方法
重叠积分可表示为 其中 其中的F函数就是前文得到的FmNN( int m ,int N, int N1 )方法,gαβ函数就是前文得到的gαβ( int La, int Lb, int λ, int α ,int β )方法,由这个公式得到了第二种计算重叠积分的方法Sab(double R,double za,double zb, int n1,int
VS2010下生成dll的方法(第二种方法)
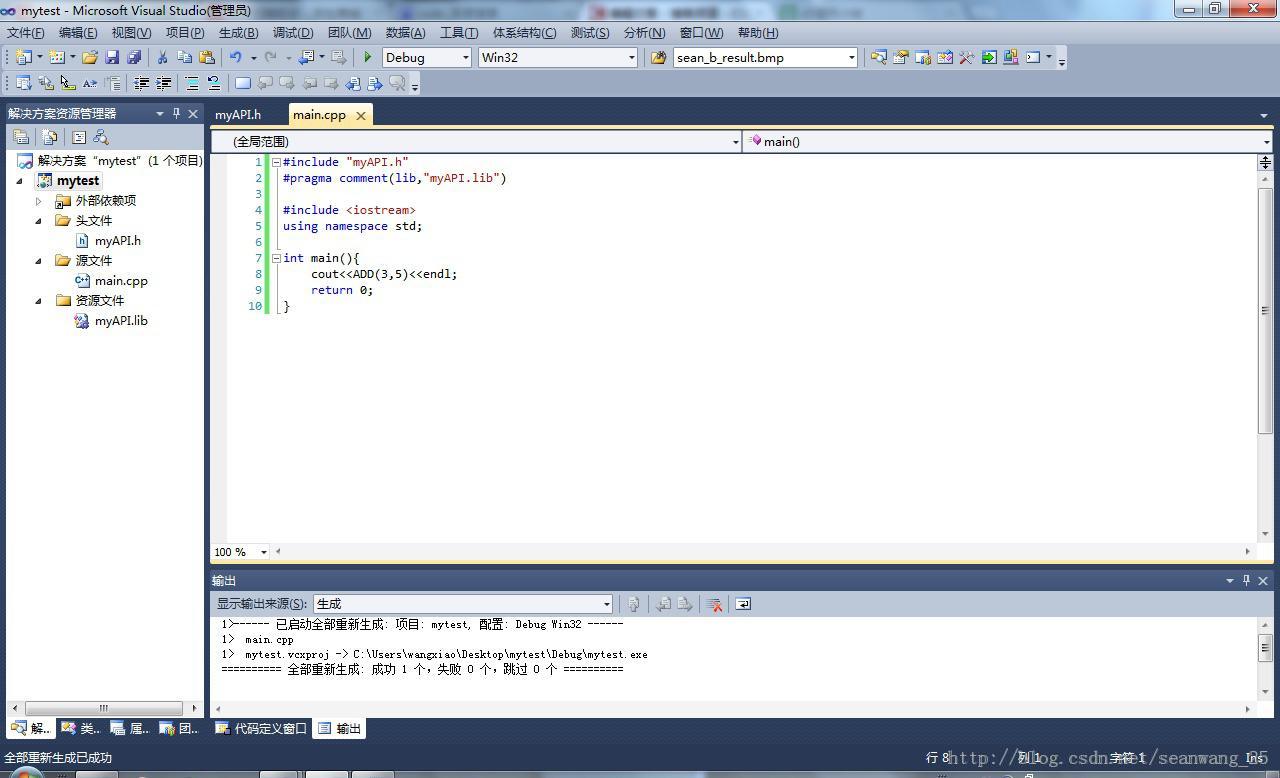
转自 http://blog.csdn.net/seanwang_25/article/details/17285505 这种模式较为简单,只用一个头文件就可以,不用dllmain.cpp和source.def文件 1.首先创建生成dll的项目:打开VS2010,两种途经建立dll项目,基于MFC DLL的和基于Win32控制台应用程序的,这里选择基于Win32控制台建立。 a
《c语言修炼内功之第二种境界(看代码就是内存)之关键字系列三》
前言:这个系列内容我会深入讲解一下c语言中的重点内容,会把每一个知识点讲的更加底层些,会增强大家的c语言内功,从内存维度看代码你会有不同的理解。这一节主要给大家讲解内存中的存储,从原码反码补码的概念开始引入,在讲更加细节的讲解数据的存储范围,从中我还会提及关键字signed和unsigned的区别,最后总结这节课讲的知识同时还有一些习题的练习以便我们更好地理解。好嘞,我们接下来开始吧。 目









![[Java] Thread 创建线程的第二种方法](/front/images/it_default.gif)