《c语言修炼内功之第二种境界（看代码就是内存）之关键字系列三》

• 前言：这个系列内容我会深入讲解一下c语言中的重点内容，会把每一个知识点讲的更加底层些，会增强大家的c语言内功，从内存维度看代码你会有不同的理解。
• 这一节主要给大家讲解内存中的存储，从原码反码补码的概念开始引入，在讲更加细节的讲解数据的存储范围，从中我还会提及关键字signed和unsigned的区别，最后总结这节课讲的知识同时还有一些习题的练习以便我们更好地理解。好嘞，我们接下来开始吧。

目录

从原反补引入

原反补之间的转化

为啥会出现补码呢？

有符号整形（signed int）和无符号整型（unsigned int）

深入理解数据在内存中的存取

存储中的判据之数据类型

内存中的存

内存中的取

有符号的存储

存储的第二种判据之大小端问题

为啥会存在大小端问题呢？

什么是大端和小端引出概念

整形数值的取值范围

总结：

从原反补引入

大家应该知道我们计算机计算的时候，使用二进制来计算的，这是因为我们计算机使用cpu来计算的，cpu只认识二进制。那既然我们知道是用二进制来计算的，那当然也是拿二进制存储的，那计算机利用二进制的存储形式是怎么样的呢？这也就是我们第一个要讲解的内容，就是原码反码补码。

 我们将数据放在内存中存储，我们就需要将我们看到的十进制数字转化成计算机认识的二进制。那我们将十进制转化成二进制叫做我们数据的原码，而保存在内存中的数据要做数据的补码（我们要打印出来的是数据的原码），显然，在我们要将它写入内存中需要原码和补码之间的转化，之后有出现了反码的概念。

• 原反补之间的转化

原码：

        正数:正数的原码为该数转化为二进制的码

        负数：负数的原码符号位为1其他位为该数正数的原码的值

反码：

       正数：正数的反码为该数转化为二进制的码

       负数：负数的符号位不变（为1），其他位按位取反（其中这与~不一样，~是把符号位也取反）

补码：

      正数：正数的补码为该数转化为二进制的码

      负数：负数的补码为该数的反码+1

小技巧：正数的原码反码补码相同，负数原码是该数的二进制（符号位为1），反码是符号位不变，其他位按位取反，补码是反码+1

这里我们对于原反补其实还有一种方法就是按照原码转化成补码的操作将补码转化成原码，答案肯定是一模一样的，那这两种方法用哪种呢？这个看个人喜好来，对于第二种其实更加符合我们在设置原反补的原理，如果按照第二种方式进行计算，我们就可以按照一条硬件电路完成转化，如下图

• 为啥会出现补码呢？

在计算机系统中，数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统一处理； 同时，加法和减法也可以统一处理（CPU 只有加法器）。此外，补码与原码相互转换，其运算过程是相同的，不需要额外的硬件电路。

有符号整形（signed int）和无符号整型（unsigned int）

为啥会有 有符号位和无符号位的区分呢？，这个我不说大家肯定也都知道，那就是因为我们的数字有正数和负数么，既然有符号位，符号位肯定就一位而且位于二进制数字的第一位，而我们将剩下的二进制位叫做数据位。

对于数字我们要进行原反补的转化，那就有 有符号位和无符号位的区分了，我们对于有符号位（signed int）就要分正数和负数，对于正数，正数的原码反码补码相同，对于负数我们要进行原反补之间的转化，那我们的符号位是否要参加计算呢？答案是肯定需要参加运算的（这里就涉及到进位的问题）。说无符号位，对于无符号位，由于没有符号位我们直接进行计算就可以不需要管第一位的问题。

深入理解数据在内存中的存取

• 存储中的判据之数据类型

int main()
{int a = 10;return 0;
}

内存中的存

•  从内存角度理解

我写这段代码的意思是将10存入int整形a里，我们从内存这样理解呢？从内存的角度我们是将计算好的二进制补码放入内存空间，空间不关心我们要存入的内容，而这里的定义变量做的初始化，做计算时只关心这个数字本身进行原码反码补码之间的转化，不关心它所存入的数据类型。所以，在我们再将数据保存在空间内的时候，数据已经被我们计算成二进制补码了。所以从数据存入内存中，数据类型的意义只有空间大小的作用。

内存中的取

•  数据类型在什么情况才会起作用呢？

那就是我们从内存中取的时候，计算机便会转化成我们所熟悉的十进制补码。

•  数据类型意义是什么呢？

我们先来举个例子比如我说我钱包里有100元，然后我问你我钱包里有多少钱，你跟我说就有100块钱人民币，其实这就是不准确的，这是因为我们没有准确说明白我钱包里的100元是人民币还是美元，欧元。

这个例子就映射到我们数据类型的意义了，当一个数字在没有说数据类型的时候无法解释某个二进制列。所以类型决定了如何解释空间内部中的二进制序列。

总结内存的存和取：

存：字面数据必须先转成补码，在放入空间当中。所以 , 所谓符号位，完全看数据本身是否携带 +- 号。和变量是否有符号

无关！

取：取数据一定要先看变量本身类型，然后才决定要不要看最高符号位。如果不需要，直接二进制转成十进制。如果需

要，则需要转成原码，然后才能识别。 ( 当然，最高符号位在哪里，又要明确大小端 )

• 有符号的存储

int main()
{signed int a = -10;printf("%d", a);return 0;
}

这个是怎么存储的呢？

首先在我们将数据放入内存空间之前，二进制的补码已经计算好。

我们先计算-10的补码

 然后将-10放入内存空间a中

 看自身类型为有符号数，我们打印为%d(按有符号打印)所以，我们在转化为原码

 所以打印就为-10；

再举一个例子：

int main()
{unsigned int a = -10;printf("%d", a);return 0;
}

放入内存前，先将-10转化为补码

 然后将-10放入内存空间a中

转化成原码

 看自身类型为无符号，在看需要打印的为%d（有符号打印），答案结果仍为-10；

 所以，这也就证明了，我们在存储的时候跟所存的数据类型无关，而取决于我们取的时候到底是以什么方式打印。

看到这个，会又有同学会问，从这里看有符号整形和无符号整型是一个意思呗？

我的答案是因为上述两个例子全部是%d打印（即有符号打印），而我们在定义变量为无符号数的时候，本身就是错误，因为两遍边类型不符，还有一点是我们在打印时要按照定义变量本身类型确定所要打印的类型，而这里无符号数打印应该用%u。接下来我们看结果。

 这个结果应该没有人会想到，因为我们一个有符号数用%u打印计算机会自动把-10当做无符号整型看待，所以打印这个数，那这个数怎么来的呢？请看下面的无符号整型存储。

• 无符号的存储

#include<stdio.h>
int main()
{unsigned int a = -10;printf("%u", a);return 0;
}

首先在我们将数据放入内存空间之前，二进制的补码已经计算好。

我们先计算-10的补码

 然后将-10放入内存空间a中

看自身类型为无符号类型，我们打印为%u打印（不需要考虑符号位），由于为%u打印计算机默认为正数，即补码就是原码，所以直接打印。

•  总结内存中的存储步骤

1. 存的时候不关心变量类型，直接将数据转化成二进制补码，直接放到空间中
2. 取的时候看自身类型，根据自身类型决定看是否看符号位同时确定原码反码补码。

• 存储的第二种判据之大小端问题

为啥会存在大小端问题呢？

我们先根据一段代码来分析

#include<stdio.h>
int main()
{int a = 0x11223344;return 0;
}

 根据我们要存储的是十六进制的11223344，而在内存中存储的是44332211。这也就是我们的大小端问题。（也就是我们在初学的时候会问为啥在内存中数据是倒着放的呢？）

我们为啥存在大小端用官方表述：

为什么会有大小端模式之分呢？这是因为在计算机系统中，我们是以字节为单位的，每个地址单元 都对应着一个字节，一个字节为8 ， 但是在 C 语言中除了 8 bit 的char之外，还有 16 bit 的 short 型， 32 bit 的 long 型（要看具体的编译器），另外，对于位数大于8 位的处理器，例如16 位或者 32 位的处理器，由于寄存器宽度大于一个字节，那么必然存在着一个如何将多个字节安排的问题。因此就 导致了大端存储模式和小端存储模式。

就如我们在选择一件事或者某个事情的时候，我们都会做不同的选择，这个大小端问题也是一样的，不同的硬件厂商有着自己的存储方式，就会存在不一样的存储，就有了大端和小端，至于是大端，这个就取决于编译器的硬件厂商，但是常见的编译器存储方式都是小端存储。

什么是大端和小端引出概念

在我们存储的时候都会有地址，那地址就会有高低之分，我们都按照地址是从低地址到高地址。同时我们的数据也会有权值位之分，什么是权值位呢？比如一个数字123，我们都知道1是百位，2是十位，3是个位，我们也将1相对于2，3来说叫做高权值位，3相对于1，2来说是低权值位。

• 大端概念

• 小端概念

这里我们可以用一个口诀来记住： 小低低（这个意思就是小端是低位低地址，剩下的后两个字不同的就为大端存储）。

int main()
{signed int a = -10;printf("%d", a);return 0;
}

整形数值的取值范围

我们这里以char为例

根据上图取值范围是-127——127，虽然是正数有0-127，负数有0-127，但是我们落下了一种就是  （符号位）1 1000 0000但我们因为计算机是不会忽略任何一种排列组合，所以计算机要用最小的成本解决更多的数据的取值范围。那这个数被我们解释成什么呢？第一种是+128第二种是-128，显然由于符号位的问题那肯定是-128，所以char的取值范围就是【-128——127】。

• 如何理解-128呢？

#include<stdio.h>
int main()
{char c = -128;printf("%d", c);return 0;
}

转化成补码

 但由于char的大小只有一个字节（8个bit位）所以会发生截断

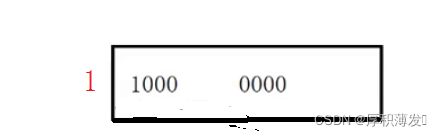
 所以就会有-128.

总结：

先看大小端，以相同的方式存，以相同的方式去取。

再看变量自身类型是否需要符号位

如果是unsigned就不需要看符号位，直接把二进制序列补码直接转化成十进制

如果是signed类型就需要看符号位

如果是0（正数）直接转化成十进制

如果是1（负数）将补码转化成原码在转化成十进制。