本文主要是介绍SLAM本质剖析-G2O(转载,感觉写得不错),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
这块还是写得不错的

转载自:https://mp.weixin.qq.com/s/NeveBIh5bb37CUyVVNocLw
SLAM本质剖析-G2O
原创 lovely_yoshino 古月居 今天
0
前言
在了解SLAM的原理、流程后,个人经常实时困惑该如何去从零开始去设计编写一套能够符合我们需求的SLAM框架。作者认为Ceres、Eigen、Sophus、G2O这几个函数库无法避免,尤其是Ceres函数库在激光SLAM和V-SLAM的优化中均有着大量的应用。
作者分别从Ceres和Eigen两个函数进行了深入的解析,这一篇文章主要对G2O函数库进行详细的阐述,来方便各位后续的开发。
(*https://blog.csdn.net/lovely_yoshino/article/details/119031125)
(*https://editor.csdn.net/md)
1
G2O示例
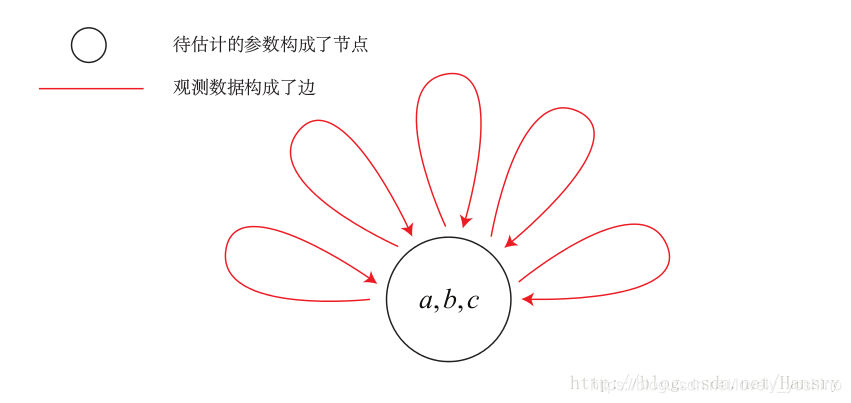
相较于Ceres而言,G2O函数库相对较为复杂,但是适用面更加广,可以解决较为复杂的重定位问题。Ceres库向通用的最小二乘问题的求解,定义优化问题,设置一些选项,可通过Ceres求解。而图优化,是把优化问题表现成图的一种方式,这里的图是图论意义上的图。一个图由若干个顶点,以及连着这些顶点的边组成。在这里,我们用顶点表示优化变量,而用边表示误差项。
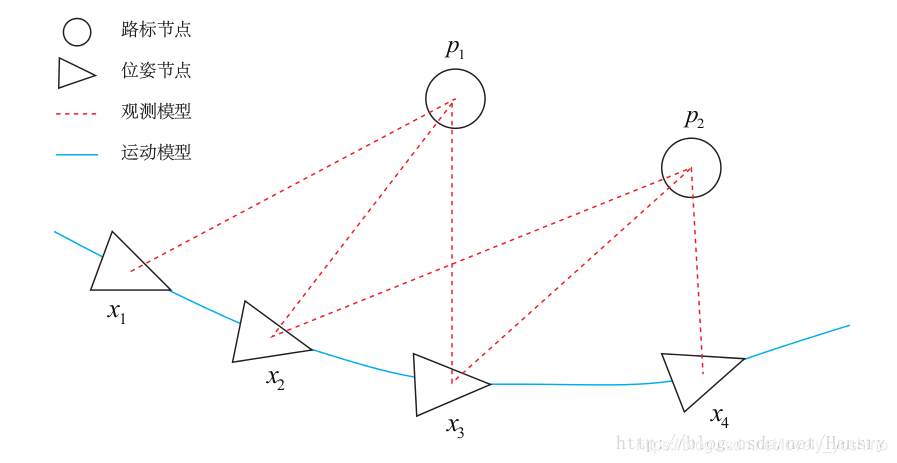
为了使用g2o,首先要将曲线拟合问题抽象成图优化。这个过程中,只要记住节点为优化变量,边为误差项即可。曲线拟合的图优化问题可以画成以下形式:
G2O在数学上主要分为四个求解步骤:

在程序中的反应为:
-
创建一个线性求解器LinearSolver。
-
创建BlockSolver,并用上面定义的线性求解器初始化。
-
创建总求解器solver,并从GN/LM/DogLeg 中选一个作为迭代策略,再用上述块求解器BlockSolver初始化。
-
创建图优化的核心:稀疏优化器(SparseOptimizer)。
-
定义图的顶点和边,并添加到SparseOptimizer中。
-
设置优化参数,开始执行优化。
#include <iostream>#include <g2o/core/base_vertex.h>#include <g2o/core/base_unary_edge.h>#include <g2o/core/block_solver.h>#include <g2o/core/optimization_algorithm_levenberg.h>#include <g2o/core/optimization_algorithm_gauss_newton.h>#include <g2o/core/optimization_algorithm_dogleg.h>#include <g2o/solvers/dense/linear_solver_dense.h>#include <Eigen/Core>#include <opencv2/core/core.hpp>#include <cmath>#include <chrono>using namespace std;// 曲线模型的顶点,模板参数:优化变量维度和数据类型(此处为自定义定点,具体可以参考下方的点定义)class CurveFittingVertex: public g2o::BaseVertex<3, Eigen::Vector3d>{public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW// 字节对齐virtual void setToOriginImpl() // 重置,设定被优化变量的原始值{_estimate << 0,0,0;}virtual void oplusImpl( const double* update ) // 更新{_estimate += Eigen::Vector3d(update);//update强制类型转换为Vector3d}// 存盘和读盘:留空virtual bool read( istream& in ) {}virtual bool write( ostream& out ) const {}};// 误差模型 模板参数:观测值维度,类型,连接顶点类型class CurveFittingEdge: public g2o::BaseUnaryEdge<1,double,CurveFittingVertex>{public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWCurveFittingEdge( double x ): BaseUnaryEdge(), _x(x) {}// 计算曲线模型误差void computeError(){const CurveFittingVertex* v = static_cast<const CurveFittingVertex*> (_vertices[0]);const Eigen::Vector3d abc = v->estimate();_error(0,0) = _measurement - std::exp( abc(0,0)*_x*_x + abc(1,0)*_x + abc(2,0) ) ;}virtual bool read( istream& in ) {}virtual bool write( ostream& out ) const {}public:double _x; // x 值, y 值为 _measurement};int main( int argc, char** argv ){double a=1.0, b=2.0, c=1.0; // 真实参数值int N=100; // 数据点double w_sigma=1.0; // 噪声Sigma值cv::RNG rng; // OpenCV随机数产生器double abc[3] = {0,0,0}; // abc参数的估计值vector<double> x_data, y_data; // 数据cout<<"generating data: "<<endl;for ( int i=0; i<N; i++ ){double x = i/100.0;x_data.push_back ( x );y_data.push_back (exp ( a*x*x + b*x + c ) + rng.gaussian ( w_sigma ));cout<<x_data[i]<<" "<<y_data[i]<<endl;}// 构建图优化,先设定g2otypedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block; // 每个误差项优化变量维度为3,误差值维度为1Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 线性方程求解器。第一步:创建一个线性求解器LinearSolver。Block* solver_ptr = new Block( linearSolver ); // 矩阵块求解器。第二步:创建BlockSolver,并用上面定义的线性求解器初始化。// 梯度下降方法,从GN, LM, DogLeg 中选g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr );//第三步:创建BlockSolver,并用上面定义的线性求解器初始化。// g2o::OptimizationAlgorithmGaussNewton* solver = new g2o::OptimizationAlgorithmGaussNewton( solver_ptr );// g2o::OptimizationAlgorithmDogleg* solver = new g2o::OptimizationAlgorithmDogleg( solver_ptr );g2o::SparseOptimizer optimizer; // 图模型。第四步:创建图优化的核心:稀疏优化器(SparseOptimizer)。optimizer.setAlgorithm( solver ); // 设置求解器optimizer.setVerbose( true ); // 打开调试输出// 往图中增加顶点。第五步:定义图的顶点和边HyperGraph,并添加到SparseOptimizer中。CurveFittingVertex* v = new CurveFittingVertex();v->setEstimate( Eigen::Vector3d(0,0,0) );v->setId(0);optimizer.addVertex( v );// 往图中增加边for ( int i=0; i<N; i++ ){CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );edge->setId(i);edge->setVertex( 0, v ); // 设置连接的顶点edge->setMeasurement( y_data[i] ); // 观测数值edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵:协方差矩阵之逆optimizer.addEdge( edge );}// 执行优化。第六步:设置优化参数,开始执行优化。cout<<"start optimization"<<endl;chrono::steady_clock::time_point t1 = chrono::steady_clock::now();optimizer.initializeOptimization();optimizer.optimize(100);chrono::steady_clock::time_point t2 = chrono::steady_clock::now();chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>( t2-t1 );cout<<"solve time cost = "<<time_used.count()<<" seconds. "<<endl;// 输出优化值Eigen::Vector3d abc_estimate = v->estimate();cout<<"estimated model: "<<abc_estimate.transpose()<<endl;return 0;}
2
G2O常见函数总结
如下图所示,这个图反应了上述的前五个步骤。
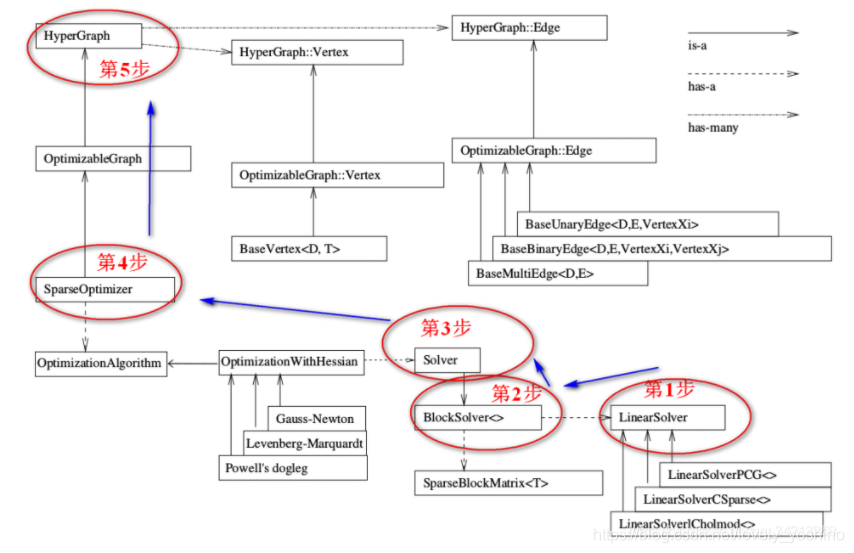
对这个结构框图做一个简单介绍(注意图中三种箭头的含义(右上角注解)):
(1)$\color{#4285f4}{图的核心:整个g2o框架可以分为上下两部分,两部分中间的连接点:SparseOpyimizer 就是整个g2o的核心部分。
(2)往上看,SparseOpyimizer其实是一个Optimizable Graph,从而也是一个超图(HyperGraph)。
(3)$\color{#4285f4}{顶点和边:}$超图有很多顶点和边。顶点继承自 Base Vertex,也即OptimizableGraph::Vertex;而边可以继承自 BaseUnaryEdge(单边), BaseBinaryEdge(双边)或BaseMultiEdge(多边),它们都叫做OptimizableGraph::Edge。
(4)$\color{#4285f4}{配置SparseOptimizer的优化算法和求解器:}$往下看,SparseOptimizer包含一个优化算法部分OptimizationAlgorithm,它是通过OptimizationWithHessian 来实现的。其中迭代策略可以从Gauss-Newton(高斯牛顿法,简称GN)、 Levernberg-Marquardt(简称LM法)、Powell’s dogleg 三者中间选择一个(常用的是GN和LM)。
(5)$\color{#4285f4}{如何求解:}$对优化算法部分进行求解的时求解器solver,它实际由BlockSolver 组成。BlockSolver由两部分组成:一个是SparseBlockMatrix,它由于求解稀疏矩阵(雅克比和海塞);另一个部分是LinearSolver,它用来求解线性方程 得到待求增量,因此这一部分是非常重要的,它可以从PCG/CSparse/Choldmod选择求解方法。
2.1 创建一个线性求解器LinearSolver
我们要求的增量方程的形式是:H△X=-b,通常情况下想到的方法就是直接求逆,也就是△X=-H.inv*b。看起来好像很简单,但这有个前提,就是H的维度较小,此时只需要矩阵的求逆就能解决问题。但是当H的维度较大时,矩阵求逆变得很困难,求解问题也变得很复杂。和Ceres类似,G2O需要一些特殊的方法对矩阵进行求逆。
这一步中我们可以选择不同的求解方式来求解线性方程,g2o中提供的求解方式主要有:
| | |
|—|—|
| LinearSolverCholmod |使用sparse cholesky分解法。继承自LinearSolverCCS|
|LinearSolverCSparse|使用CSparse法。继承自LinearSolverCCS|
|LinearSolverDense|使用dense cholesky分解法。继承自LinearSolver|
|LinearSolverEigen|依赖项只有eigen,使用eigen中sparse Cholesky 求解,因此编译好后可以方便的在其他地方使用,性能和CSparse差不多。继承自LinearSolver|
|LinearSolverPCG |使用preconditioned conjugate gradient 法,继承自LinearSolver |
2.2 创建BlockSolver。并用上面定义的线性求解器初始化
BlockSolver 内部包含 LinearSolver,用上面我们定义的线性求解器LinearSolver来初始化。它的定义在如下文件夹内:
g2o/g2o/core/block_solver.h你点进去会发现 BlockSolver有两种定义方式:
一种是指定的固定变量的solver,我们来看一下定义:
using BlockSolverPL = BlockSolver< BlockSolverTraits<p, l> >;其中p代表pose的维度(注意一定是流形manifold下的最小表示),l表示landmark的维度。
另一种是可变尺寸的solver,定义如下:
using BlockSolverX = BlockSolverPL<Eigen::Dynamic, Eigen::Dynamic>;block_solver.h的最后,预定义了比较常用的几种类型。
BlockSolver_6_3 :表示pose 是6维,观测点是3维。用于3D SLAM中的BABlockSolver_7_3:在BlockSolver_6_3 的基础上多了一个scaleBlockSolver_3_2:表示pose 是3维,观测点是2维
2.3 创建总求解器solver。并从GN, LM, DogLeg 中选一个,再用上述块求解器BlockSolver初始化
我们来看g2o/g2o/core/ 目录下,发现Solver的优化方法有三种:分别是高斯牛顿(GaussNewton)法,LM(Levenberg–Marquardt)法、Dogleg法,如下图所示,也和前面的图相匹配。
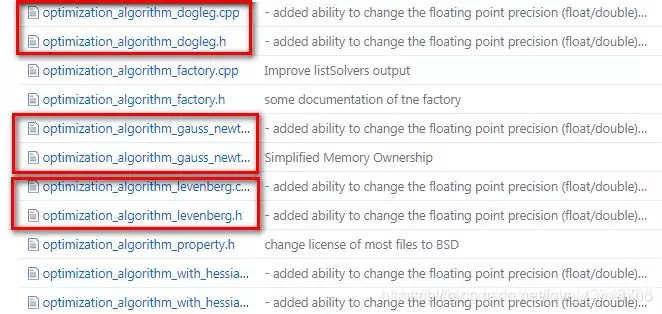
点进去 GN、 LM、 Doglet算法内部,会发现他们都继承自同一个类:OptimizationWithHessian,如下图所示,这也和我们最前面那个图是相符的。
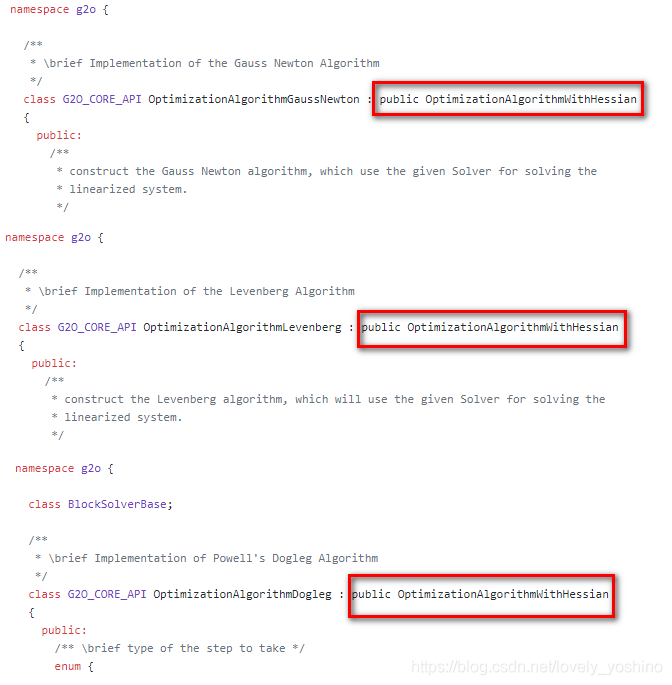
点进去看 OptimizationAlgorithmWithHessian,发现它又继承自OptimizationAlgorithm,这也和前面的相符。
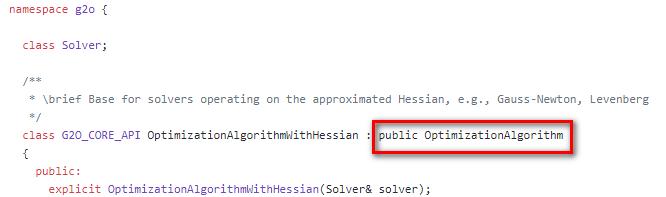
在该阶段可以选择三种方法:
g2o::OptimizationAlgorithmGaussNewtong2o::OptimizationAlgorithmLevenbergg2o::OptimizationAlgorithmDogleg
2.4 创建终极大boss 稀疏优化器(SparseOptimizer),并用已定义求解器作为求解方法
创建稀疏优化器:
g2o::SparseOptimizer optimizer;用前面定义好的求解器作为求解方法:
SparseOptimizer::setAlgorithm(OptimizationAlgorithm* algorithm)其中setVerbose是设置优化过程输出信息用的。
SparseOptimizer::setVerbose(bool verbose)不信我们来看一下它的定义。

2.5 定义图的顶点和边。并添加到SparseOptimizer中
$\color{#4285f4}{点 Vertex}$
在g2o中定义Vertex有一个通用的类模板:BaseVertex。在结构框图中可以看到它的位置就是HyperGraph继承的根源。
同时在图中我们注意到BaseVertex具有两个参数D/T,这两个参数非常重要,我们来看一下:
D 是int 类型,表示vertex的最小维度,例如3D空间中旋转是3维的,则 D = 3
T 是待估计vertex的数据类型,例如用四元数表达三维旋转,则 T 就是Quaternion 类型
static const int Dimension = D; ///< dimension of the estimate (minimal) in the manifold spacetypedef T EstimateType;EstimateType _estimate;如何自己定义Vertex
在我们动手定义自己的Vertex之前,可以先看下g2o本身已经定义了一些常用的顶点类型:
VertexSE2 : public BaseVertex<3, SE2> //2D pose Vertex, (x,y,theta)VertexSE3 : public BaseVertex<6, Isometry3> //Isometry3使欧式变换矩阵T,实质是4*4矩阵//6d vector (x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion)VertexPointXY : public BaseVertex<2, Vector2>VertexPointXYZ : public BaseVertex<3, Vector3>VertexSBAPointXYZ : public BaseVertex<3, Vector3>// SE3 Vertex parameterized internally with a transformation matrix and externally with its exponential mapVertexSE3Expmap : public BaseVertex<6, SE3Quat>// SBACam Vertex, (x,y,z,qw,qx,qy,qz),(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion.// qw is assumed to be positive, otherwise there is an ambiguity in qx,qy,qz as a rotationVertexCam : public BaseVertex<6, SBACam>// Sim3 Vertex, (x,y,z,qw,qx,qy,qz),7d vector,(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion.VertexSim3Expmap : public BaseVertex<7, Sim3>
但是!如果在使用中发现没有我们可以直接使用的Vertex,那就需要自己来定义了。一般来说定义Vertex需要重写这几个函数(注意注释):
virtual bool read(std::istream& is);virtual bool write(std::ostream& os) const;// 分别是读盘、存盘函数,一般情况下不需要进行读/写操作的话,仅仅声明一下就可以virtual void oplusImpl(const number_t* update);//顶点更新函数virtual void setToOriginImpl();//顶点重置函数,设定被优化变量的原始值。
请注意里面的oplusImpl函数,是非常重要的函数,主要用于优化过程中增量△x 的计算。根据增量方程计算出增量后,通过这个函数对估计值进行调整,因此该函数的内容要重视。
根据上面四个函数可以得到定义顶点的基本格式:
class myVertex: public g2o::BaseVertex<Dim, Type>{public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWmyVertex(){}virtual void read(std::istream& is) {}virtual void write(std::ostream& os) const {}virtual void setOriginImpl(){_estimate = Type();}virtual void oplusImpl(const double* update) override{_estimate += update;}}
另外值得注意的是,优化变量更新并不是所有时候都可以像上面两个一样直接 += 就可以,这要看优化变量使用的类型(是否对加法封闭)。
向图中添加顶点
接着上面定义完的顶点,我们把它添加到图中:
CurveFittingVertex* v = new CurveFittingVertex();v->setEstimate( Eigen::Vector3d(0,0,0) );// 设定初始值v->setId(0); // 定义节点编号optimizer.addVertex( v ); // 把节点添加到图中
$\color{#4285f4}{边 Edge}$
图优化中的边:BaseUnaryEdge,BaseBinaryEdge,BaseMultiEdge 分别表示一元边,两元边,多元边。
顾名思义,一元边可以理解为一条边只连接一个顶点,两元边理解为一条边连接两个顶点(常见),多元边理解为一条边可以连接多个(3个以上)顶点。
以最常见的二元边为例分析一下他们的参数:D, E, VertexXi, VertexXj:
-
D 是 int 型,表示测量值的维度 (dimension)
-
E 表示测量值的数据类型
-
VertexXi,VertexXj 分别表示不同顶点的类型
BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>上面这行代码表示二元边,参数1是说测量值是2维的;参数2对应测量值的类型是Vector2D,参数3和4表示两个顶点也就是优化变量分别是三维点 VertexSBAPointXYZ,和李群位姿VertexSE3Expmap。
如何定义一个边
除了上面那行定义语句,还要复写一些重要的成员函数:
virtual bool read(std::istream& is);virtual bool write(std::ostream& os) const;// 分别是读盘、存盘函数,一般情况下不需要进行读/写操作的话,仅仅声明一下就可以virtualvoid computeError();// 非常重要,是使用当前顶点值计算的测量值与真实测量值之间的误差virtual void linearizeOplus();// 非常重要,是在当前顶点的值下,该误差对优化变量的偏导数,也就是Jacobian矩阵
除了上面四个函数,还有几个重要的成员变量以及函数:
_measurement;// 存储观测值_error; // 存储computeError() 函数计算的误差_vertices[]; // 存储顶点信息,比如二元边,_vertices[]大小为2//存储顺序和调用setVertex(int, vertex) 和设定的int有关(0或1)setId(int); // 定义边的编号(决定了在H矩阵中的位置)setMeasurement(type); // 定义观测值setVertex(int, vertex); // 定义顶点setInformation(); // 定义协方差矩阵的逆
有了上面那些重要的成员变量和成员函数,就可以用来定义一条边了:
class myEdge: public g2o::BaseBinaryEdge<errorDim, errorType, Vertex1Type, Vertex2Type>{public:EIGEN_MAKE_ALIGNED_OPERATOR_NEWmyEdge(){}virtual bool read(istream& in) {}virtual bool write(ostream& out) const {}virtual void computeError() override{// ... _error = _measurement - Something;}virtual void linearizeOplus() override // 求误差对优化变量的偏导数,雅克比矩阵 {_jacobianOplusXi(pos, pos) = something;// .../* _jocobianOplusXj(pos, pos) = something; ... */}private:data}
向图中添加边
和添加点有一点类似,下面是添加一元边:
// 往图中增加边 for ( int i=0; i<N; i++ ){CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] );edge->setId(i);edge->setVertex( 0, v ); // 设置连接的顶点edge->setMeasurement( y_data[i] ); // 观测数值edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵:协方差矩阵之逆optimizer.addEdge( edge );
但在SLAM中我们经常要使用的二元边(前后两个位姿),那么此时:
index = 1;for ( const Point2f p:points_2d ){g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();edge->setId ( index ); // 边的b编号edge->setVertex ( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> ( optimizer.vertex ( index ) ) );edge->setVertex ( 1, pose );edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) ); // 设置观测的特征点图像坐标edge->setParameterId ( 0,0 );edge->setInformation ( Eigen::Matrix2d::Identity() );optimizer.addEdge ( edge );index++;}
2.6设置优化参数,开始执行优化
设置SparseOptimizer的初始化、迭代次数、保存结果等。
初始化:
SparseOptimizer::initializeOptimization(HyperGraph::EdgeSet& eset)设置迭代次数,然后就开始执行图优化了。
SparseOptimizer::optimize(int iterations, bool online)3
G2O 相机位姿优化
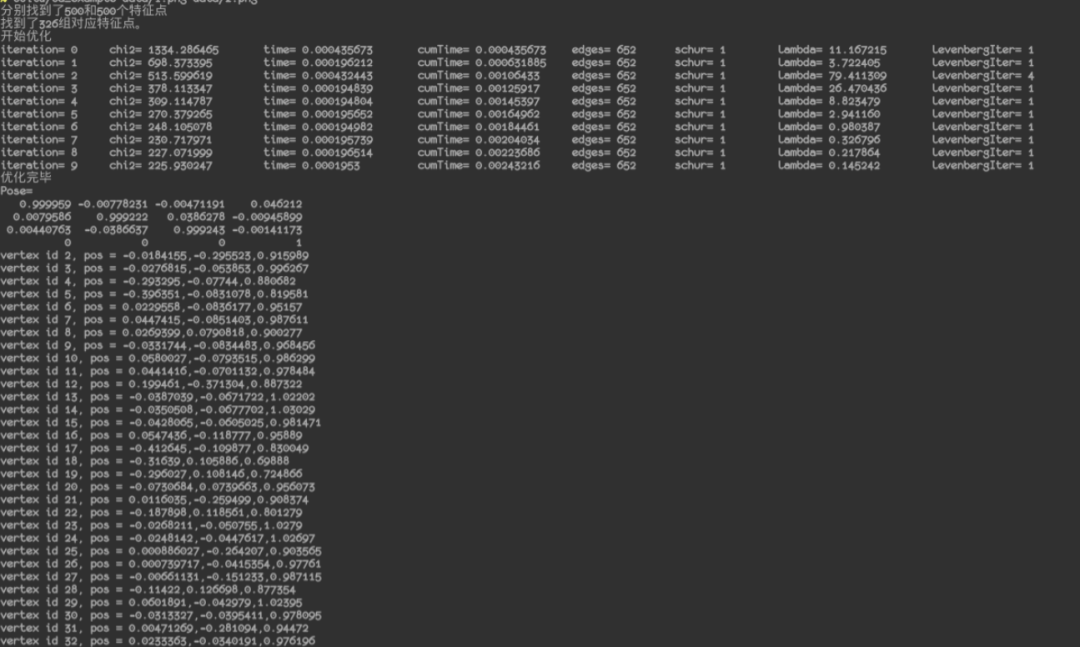
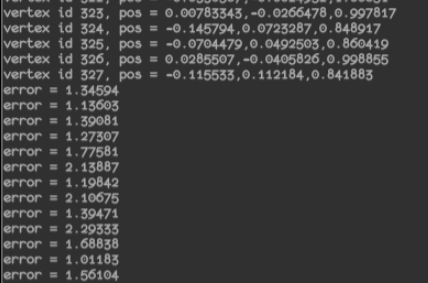
/*** BA Example* Author: Xiang Gao* Date: 2016.3* Email: gaoxiang12@mails.tsinghua.edu.cn** 在这个程序中,我们读取两张图像,进行特征匹配。然后根据匹配得到的特征,计算相机运动以及特征点的位置。这是一个典型的Bundle Adjustment,我们用g2o进行优化。*/// for std#include <iostream>// for opencv#include <opencv2/core/core.hpp>#include <opencv2/highgui/highgui.hpp>#include <opencv2/features2d/features2d.hpp>#include <boost/concept_check.hpp>// for g2o#include <g2o/core/sparse_optimizer.h>#include <g2o/core/block_solver.h>#include <g2o/core/robust_kernel.h>#include <g2o/core/robust_kernel_impl.h>#include <g2o/core/optimization_algorithm_levenberg.h>#include <g2o/solvers/cholmod/linear_solver_cholmod.h>#include <g2o/types/slam3d/se3quat.h>#include <g2o/types/sba/types_six_dof_expmap.h>using namespace std;// 寻找两个图像中的对应点,像素坐标系// 输入:img1, img2 两张图像// 输出:points1, points2, 两组对应的2D点int findCorrespondingPoints( const cv::Mat& img1, const cv::Mat& img2, vector<cv::Point2f>& points1, vector<cv::Point2f>& points2 );// 相机内参double cx = 325.5;double cy = 253.5;double fx = 518.0;double fy = 519.0;int main( int argc, char** argv ){// 调用格式:命令 [第一个图] [第二个图]if (argc != 3){cout<<"Usage: ba_example img1, img2"<<endl;exit(1);}// 读取图像cv::Mat img1 = cv::imread( argv[1] );cv::Mat img2 = cv::imread( argv[2] );// 找到对应点vector<cv::Point2f> pts1, pts2;if ( findCorrespondingPoints( img1, img2, pts1, pts2 ) == false ){cout<<"匹配点不够!"<<endl;return 0;}cout<<"找到了"<<pts1.size()<<"组对应特征点。"<<endl;// 构造g2o中的图// 先构造求解器g2o::SparseOptimizer optimizer;// 使用Cholmod中的线性方程求解器g2o::BlockSolver_6_3::LinearSolverType* linearSolver = new g2o::LinearSolverCholmod<g2o::BlockSolver_6_3::PoseMatrixType> ();// 6*3 的参数g2o::BlockSolver_6_3* block_solver = new g2o::BlockSolver_6_3( linearSolver );// L-M 下降g2o::OptimizationAlgorithmLevenberg* algorithm = new g2o::OptimizationAlgorithmLevenberg( block_solver );optimizer.setAlgorithm( algorithm );optimizer.setVerbose( false );// 添加节点// 两个位姿节点for ( int i=0; i<2; i++ ){g2o::VertexSE3Expmap* v = new g2o::VertexSE3Expmap();v->setId(i);if ( i == 0)v->setFixed( true ); // 第一个点固定为零// 预设值为单位Pose,因为我们不知道任何信息v->setEstimate( g2o::SE3Quat() );optimizer.addVertex( v );}// 很多个特征点的节点// 以第一帧为准for ( size_t i=0; i<pts1.size(); i++ ){g2o::VertexSBAPointXYZ* v = new g2o::VertexSBAPointXYZ();v->setId( 2 + i );// 由于深度不知道,只能把深度设置为1了double z = 1;double x = ( pts1[i].x - cx ) * z / fx;double y = ( pts1[i].y - cy ) * z / fy;v->setMarginalized(true);v->setEstimate( Eigen::Vector3d(x,y,z) );optimizer.addVertex( v );}// 准备相机参数g2o::CameraParameters* camera = new g2o::CameraParameters( fx, Eigen::Vector2d(cx, cy), 0 );camera->setId(0);optimizer.addParameter( camera );// 准备边// 第一帧vector<g2o::EdgeProjectXYZ2UV*> edges;for ( size_t i=0; i<pts1.size(); i++ ){g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();edge->setVertex( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> (optimizer.vertex(i+2)) );edge->setVertex( 1, dynamic_cast<g2o::VertexSE3Expmap*> (optimizer.vertex(0)) );edge->setMeasurement( Eigen::Vector2d(pts1[i].x, pts1[i].y ) );edge->setInformation( Eigen::Matrix2d::Identity() );edge->setParameterId(0, 0);// 核函数edge->setRobustKernel( new g2o::RobustKernelHuber() );optimizer.addEdge( edge );edges.push_back(edge);}// 第二帧for ( size_t i=0; i<pts2.size(); i++ ){g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();edge->setVertex( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> (optimizer.vertex(i+2)) );edge->setVertex( 1, dynamic_cast<g2o::VertexSE3Expmap*> (optimizer.vertex(1)) );edge->setMeasurement( Eigen::Vector2d(pts2[i].x, pts2[i].y ) );edge->setInformation( Eigen::Matrix2d::Identity() );edge->setParameterId(0,0);// 核函数edge->setRobustKernel( new g2o::RobustKernelHuber() );optimizer.addEdge( edge );edges.push_back(edge);}cout<<"开始优化"<<endl;optimizer.setVerbose(true);optimizer.initializeOptimization();optimizer.optimize(10);cout<<"优化完毕"<<endl;//我们比较关心两帧之间的变换矩阵g2o::VertexSE3Expmap* v = dynamic_cast<g2o::VertexSE3Expmap*>( optimizer.vertex(1) );Eigen::Isometry3d pose = v->estimate();cout<<"Pose="<<endl<<pose.matrix()<<endl;// 以及所有特征点的位置for ( size_t i=0; i<pts1.size(); i++ ){g2o::VertexSBAPointXYZ* v = dynamic_cast<g2o::VertexSBAPointXYZ*> (optimizer.vertex(i+2));cout<<"vertex id "<<i+2<<", pos = ";Eigen::Vector3d pos = v->estimate();cout<<pos(0)<<","<<pos(1)<<","<<pos(2)<<endl;}// 估计inlier的个数int inliers = 0;for ( auto e:edges ){e->computeError();// chi2 就是 error*\Omega*error, 如果这个数很大,说明此边的值与其他边很不相符if ( e->chi2() > 1 ){cout<<"error = "<<e->chi2()<<endl;}else{inliers++;}}cout<<"inliers in total points: "<<inliers<<"/"<<pts1.size()+pts2.size()<<endl;optimizer.save("ba.g2o");return 0;}int findCorrespondingPoints( const cv::Mat& img1, const cv::Mat& img2, vector<cv::Point2f>& points1, vector<cv::Point2f>& points2 ){cv::ORB orb;vector<cv::KeyPoint> kp1, kp2;cv::Mat desp1, desp2;orb( img1, cv::Mat(), kp1, desp1 );orb( img2, cv::Mat(), kp2, desp2 );cout<<"分别找到了"<<kp1.size()<<"和"<<kp2.size()<<"个特征点"<<endl;cv::Ptr<cv::DescriptorMatcher> matcher = cv::DescriptorMatcher::create( "BruteForce-Hamming");double knn_match_ratio=0.8;vector< vector<cv::DMatch> > matches_knn;matcher->knnMatch( desp1, desp2, matches_knn, 2 );vector< cv::DMatch > matches;for ( size_t i=0; i<matches_knn.size(); i++ ){if (matches_knn[i][0].distance < knn_match_ratio * matches_knn[i][1].distance )matches.push_back( matches_knn[i][0] );}if (matches.size() <= 20) //匹配点太少return false;for ( auto m:matches ){points1.push_back( kp1[m.queryIdx].pt );points2.push_back( kp2[m.trainIdx].pt );}return true;}
最后显示了特征点的数量,估计的位姿变换,以及各特征点的空间位置。最后,还显示了inliers的数量。
4
李代数二维&三维转化
g2o::SE3Quat SE2ToSE3(const g2o::SE2& _se2){SE3Quat ret;ret.setTranslation(Eigen::Vector3d(_se2.translation()(0), _se2.translation()(1), 0));ret.setRotation(Eigen::Quaterniond(AngleAxisd(_se2.rotation().angle(), Vector3d::UnitZ())));return ret;}g2o::SE2 SE3ToSE2(const SE3Quat &_se3){Eigen::Vector3d eulers = g2o::internal::toEuler(_se3.rotation().matrix());return g2o::SE2(_se3.translation()(0), _se3.translation()(1), eulers(2));}
参考链接:
https://www.jianshu.com/p/7d4b570af5ed
https://blog.csdn.net/hansry/article/details/74980709
https://blog.csdn.net/orange_littlegirl/article/details/88700834
https://blog.csdn.net/electech6/article/details/86534426
这篇关于SLAM本质剖析-G2O(转载,感觉写得不错)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





