本文主要是介绍【深度强化学习】TRPO、PPO,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
策略梯度的缺点
-
步长难以确定,一旦步长选的不好,就导致恶性循环
步长不合适 → 策略变差 → 采集的数据变差 → (回报 / 梯度导致的)步长不合适 步长不合适 \to 策略变差 \to 采集的数据变差 \to (回报/梯度导致的)步长不合适 步长不合适→策略变差→采集的数据变差→(回报/梯度导致的)步长不合适 -
一阶信息不限制步长容易越过局部最优,而且很难回来
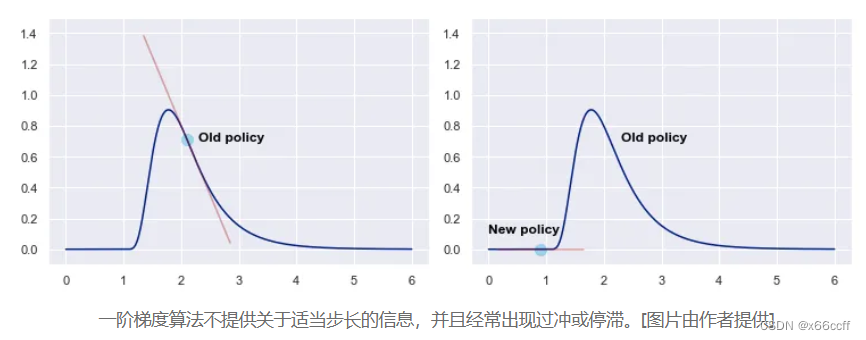
TRPO 置信域策略优化
思想:
- 步子不要太大,应该保证更新在某个邻域内 ∣ ∣ θ − θ o l d ∣ ∣ < Δ ||\theta-\theta_{old}||<\Delta ∣∣θ−θold∣∣<Δ(或者 K L ( π θ ( ⋅ ∣ ⋅ ) ) , π θ o l d ( ⋅ ∣ ⋅ ) ) < Δ \mathrm{KL}(\pi_\theta(\cdot|\cdot)),\pi_{\theta_{old}}(\cdot|\cdot))<\Delta KL(πθ(⋅∣⋅)),πθold(⋅∣⋅))<Δ)
- 利用二阶信息估计邻域 N ( θ o l d ) \mathcal{N}(\theta_{old}) N(θold) 内的 θ \theta θ
步骤
- 对循环的每一步,用 θ o l d \theta_{old} θold 策略采样一条轨迹(MC 思想)
- 对每一个轨迹位置,都计算它们的折扣回报 G i G_i Gi
- 用采样的样本估计期望作为近似的目标函数 L ( θ ∣ θ o l d ) L(\theta|\theta_{old}) L(θ∣θold)(除以 π o l d \pi_{old} πold是因为重要性采样)
L ( θ ∣ θ o l d ) = E a i ∼ π [ π ( a i ∣ s i ; θ ) G i ] L(\theta|\theta_{old}) = \mathbb{E}_{a_i\sim\pi}[{\pi(a_i|s_i;\theta)}G_i] L(θ∣θold)=Eai∼π[π(ai∣si;θ)Gi]
L ( θ ∣ θ o l d ) = E a i ∼ π o l d [ π ( a i ∣ s i ; θ ) π ( a i ∣ s i ; θ o l d ) G i ] \red{L(\theta|\theta_{old}) = \mathbb{E}_{a_i\sim\pi_{old}}[\frac{\pi(a_i|s_i;\theta)}{\pi(a_i|s_i;\theta_{old})}G_i]} L(θ∣θold)=Eai∼πold[π(ai∣si;θold)π(ai∣si;θ)Gi] - 利用某种(二阶)优化方法(涉及 Fisher Information Matrix、共轭梯度法)求邻域内的能够最大化近似代价函数的最大值

优势:
- 训练更稳定,收敛曲线不会剧烈波动,而且对超参数不敏感
- 样本有效,用更少的经验就能达到和 PG 相同的表现
缺点:
- 重要性采样:除法引起高方差
- 有约束优化问题,不容易优化
PPO 近端策略优化
PPO 实际上就是为了解决 TRPO 的这两个问题而提出的,做的改进是:
- Clip 截断重要性采样的值,防止过大(类似于梯度截断)
C l i p { π ( a i ∣ s i ; θ ) π ( a i ∣ s i ; θ o l d ) , 1 − ϵ , 1 + ϵ } \mathrm{Clip} \left\{ \frac{\pi(a_i|s_i;\theta)}{\pi(a_i|s_i;\theta_{old})} , 1-\epsilon, 1+\epsilon \right\} Clip{π(ai∣si;θold)π(ai∣si;θ),1−ϵ,1+ϵ} - KL散度条件转为无约束,自适应 β \beta β超参
max θ L ( θ ∣ θ o l d ) − β K L ( θ ∣ θ o l d ) \max_\theta L(\theta|\theta_{old}) - \beta \mathrm{KL} (\theta|\theta_{old}) θmaxL(θ∣θold)−βKL(θ∣θold)
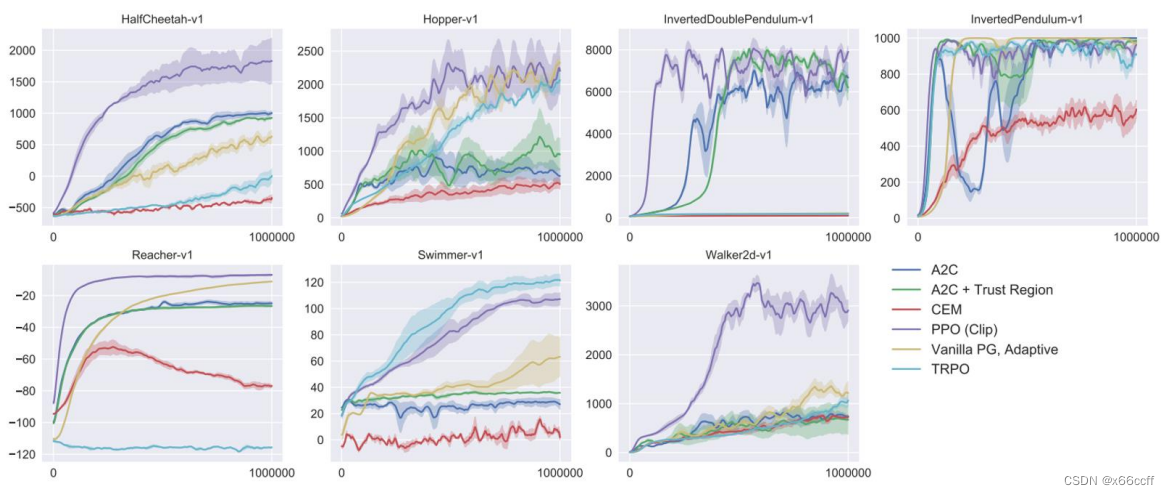
总结
策略梯度
REINFORCE (MC,从梯度上升开始、除以 π \pi π变成 Ln)
REINFORCE → 基线 REINFORCE (MC, G − v ( s ) G-v(s) G−v(s))→ Actor-Critic(TD, r + γ v ( s ) − v ( s ′ ) r+γv(s)-v(s') r+γv(s)−v(s′))
REINFORCE → TRPO (有约束、二阶信息)→ PPO(有约束转无约束、截断重要性)
REINFORCE → …
More
https://spinningup.openai.com/en/latest/algorithms/trpo.html
https://jonathan-hui.medium.com/rl-the-math-behind-trpo-ppo-d12f6c745f33
https://towardsdatascience.com/trust-region-policy-optimization-trpo-explained-4b56bd206fc2
这篇关于【深度强化学习】TRPO、PPO的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





