【深度强化学习】DQN, Double DQN, Dueling DQN

本文主要是介绍【深度强化学习】DQN, Double DQN, Dueling DQN，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

DQN

更新方程

$Q_{\theta }(s_t,a_t)\leftarrow Q_{\theta }(s_t,a_t)+\alpha \left(r_t+\gamma {\max }_{a^{\prime }}{Q}_{\theta }(s_{t+1},a^{\prime })-Q_{\theta }(s_t,a_t)\right)$

缺点：

1. 频繁更新，算法不稳定
2. 数据并不满足 i.i.d.

解决方法

• 经验回放
• 双网络结构（评估网络、目标网络）

经验回放

直觉：利用记忆，降低方差，增加稳定性。
做法：训练过程中存储$(s,a,r,s^{\prime })$ 到 buffer，训练的时候均匀/非均匀采样

优先经验回放（PER）

直觉：样本的TD 误差也不同，并且样本数量也不同。
如：打游戏，一般的关卡打小怪，比较容易，TD loss 很小，训练样本也多；最后一关打boss，难度大， TD loss 大，训练样本也少。
因此我们需要调整样本的采样概率，TD loss 大的样本给更大的采样概率，并给较小的学习率。
我们存储数据到 Buffer 的时候，还额外存储一个采样概率 $p_t+ϵ$

$$p_t=|{\delta }_t|$$
${\delta }_t$代表这个样本的TD loss

选中概率
$$P(t)=\frac{p_t^{\alpha }}{{\sum }_k{p}_k^{\alpha }}$$

重要性采样调整学习率
$${\omega }_t=\frac{(N\times P(t){)}^{-\beta }}{{\max }_i{\omega }_i}$$

双网络结构

直觉：避免使用自举法，自己评价自己。这样 label 背后的机制在一段时间内总是稳定的，部分解决了DQN的偏差大的问题。
用慢 Q 网络计算 TD target
$$目标=r_t+\gamma \underset{a^{\prime }}{\max }{Q}_{\theta -}(s_{t+1},a^{\prime })$$

---

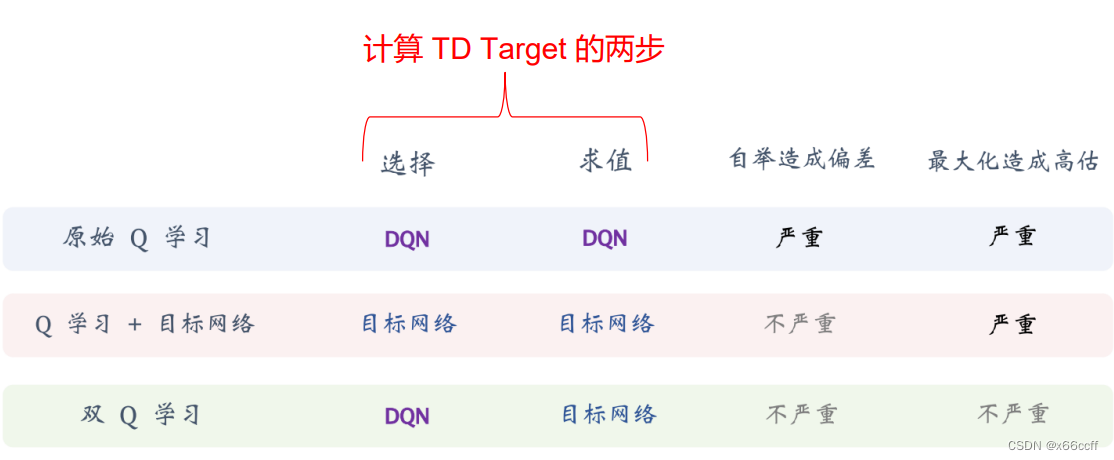
Double DQN

但是使用了双网络（慢Q用来计算 TD target）之后，由于仍然使用 max 操作，会有**过估计的问题，导致算法容易过于自信，**高估$q_{\ast }(s,a)$ 的值。因此使用 Double DQN，对 TD target 的 max 重写为 argmax 的形式

DQN（快慢双Q、慢Q计算TD）
$$y_t=r_r+\gamma Q_{\theta -}(s_{t+1},\arg \underset{a^{\prime }}{\max }{Q}_{\theta -}(s_{t+1},a^{\prime }))$$

Double DQN（快慢双Q、慢Q只评估TD值、快Q计算max动作）
$$y_t=r_r+\gamma Q_{\theta -}(s_{t+1},\arg \underset{a^{\prime }}{\max }{Q}_{\theta }(s_{t+1},a^{\prime }))$$

---

Dueling DQN

我们继续往 Double DQN 里面引入另外的模型假设，就有可能继续提升模型的性能：

这里的假设/直觉是：
部分环境反馈 Q 可能仅与状态 s 有关，和 a 无关。换句话说：$Q(s,a_1)$ 和 $Q(s,a_2)$ 之间并不是完全无关的，对于部分反馈，他们之间是正相关的。
例子：

s = 小明考试得 0 分
a1 = 小明不做任何事
a2 = 小明和妈妈说“妈妈我爱你”Q(s,a1) < 0 这是显然的
Q(s,a2) < 0 也同样有很大可能发生

在上面的例子中，如果我们独立地估计两个值，那么在估计第二个 Q 值的时候，TD loss 会比没有使用 Dueling 大（因为 Dueling 已经可以用$V(s)$作为一个 baseline 估计），因为在这个场景下，Q 很大程度由 s 决定，如果能整体地学习 Q 关于 a 的加权函数，比如说 ${\sum }_a\pi (a|s)Q(s,a)$ ，也就是 $V(s)$，那么可以预期模型的收敛速度会加快。

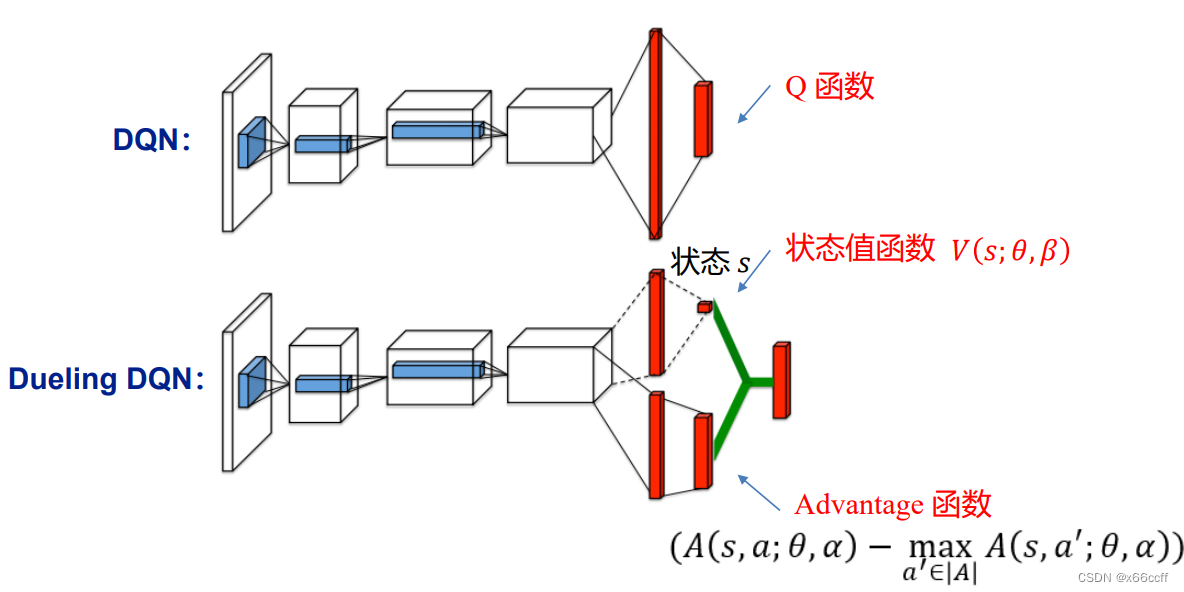
因此，Dueling DQN 使用两个网络，Q被表示为两个网络的输出的和
$$Q(s,a)=A(s,a)+V(s)$$
这里 $A$ 被称作优势函数，$A$ 相对于单纯的 $Q$ 更强调动作$a$的好坏，而$V$只关注状态的好坏。

不同的优势函数聚合形式

这篇关于【深度强化学习】DQN, Double DQN, Dueling DQN的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---