本文主要是介绍深度学习——第6章 浅层神经网络(NN),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
第6章 浅层神经网络(NN)
目录
6.1 神经网络模型概述
6.2 神经网络正向传播
6.3 神经网络反向传播
6.4 W和b的初始化
6.5 总结
上一课主要介绍了一些神经网络必备的基础知识,包括Sigmoid激活函数、损失函数、梯度下降和计算图。这些知识对学习神经网络非常有用。本节将开始真正的神经网络学习,从一个浅层的神经网络出发,详细推导其正向传播和反向传播完整过程。
6.1 神经网络模型概述
首先,我们来看一个简单的神经网络模型:
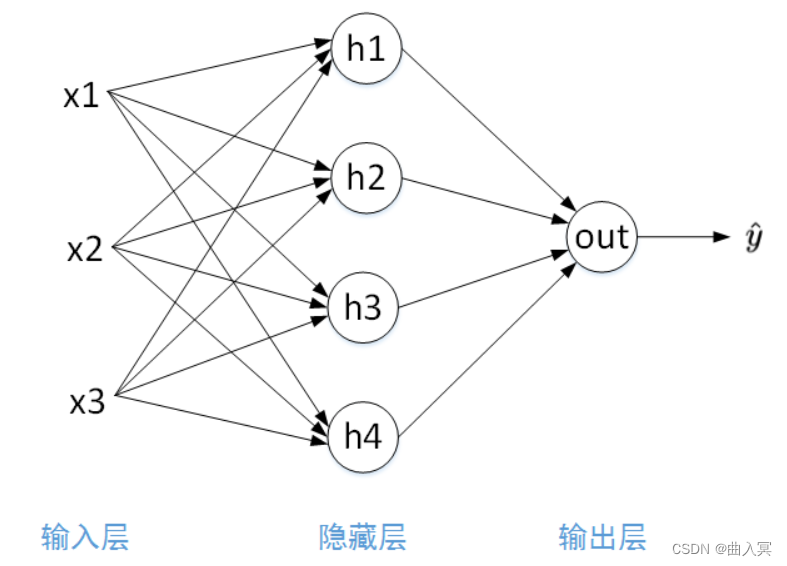
最简单的神经网络模型由输入层(Input Layer)、隐藏层(Hidden Layer)、输出层(Output Layer)组成,我们称之为2层神经网络。隐藏层和输出层都由个数不一的神经元组成。如上图所示,输入层有3个输入:x1、x2、x3,分别代表不同的输入特征。例如一张图片所有的像素值(当然不止3个)。一般地,输入层不标注 ◯ \bigcirc ◯,表示没有神经元。该神经网络模型隐藏层包含了4个神经元,输出层只有1个神经元。
需要特别注意的是,在解决二分类或者预测问题时,输出层神经元个数为1。如果是多分类问题,输出层就需要多个神经元。这里先介绍最简单的神经网络模型,多分类问题之后再详细介绍。
第1章已经介绍过单个神经元的结构:

单个神经元包含参数 W W W和 b b b,分别称之为权重系数(参数)和常数项。 W W W的维度与输入 x x x的维度相同, b b b是单个元素的标量。神经元整个计算过程分成两部分:线性计算和非线性计算。
我们来看上面的神经网络模型,输入层矩阵 x x x的维度是(3,1)。通常我们习惯把 X X X记为 a [ 0 ] a^{[0]} a[0],上标[0]表示输入层。因为输入层没有神经元计算,所以用0标注。隐藏层有4个神经元,每个神经元均与 a [ 0 ] a^{[0]} a[0] 连接。因此,隐藏层的权重系数 W [ 1 ] W^{[1]} W[1]的维度是(4,3),注意这里的上标[1]表示隐藏层。隐藏层的常数项 b [ 1 ] b^{[1]} b[1]的维度是(4,1)。输出层只有1个神经元,与4个隐藏层神经元相连接。因此,输出层的权重
数 W [ 2 ] W^{[2]} W[2]的维度是(1,4),上标[2]表示输出层。同理,输出层常数项 b [ 2 ] b^{[2]} b[2]的维度是(1,1),即只有一个元素。
神经网络每次迭代训练由正向传播和反向传播两部分组成。正向传播就是训练样本数据通过输入层–>隐藏层–>输出层,经过各层神经元计算后得到预测值,预测值与真实样本标签误差产生损失函数。然后,再进行反向传播。为了让损失函数减小,利用梯度下降算法,更新权重系数 W W W和常数项 b b b。这样就完成了一次迭代训练。经过多次的迭代训练之后,通常能使损失函数逐渐减小,最终确定最优化时对应的 W W W和 b b b。这样,整个神经网络的训练过程就结束了。
6.2 神经网络正向传播
知道了输入 x x x,参数 W [ 1 ] W^{[1]} W[1]、 b [ 1 ] b^{[1]} b[1]、 W [ 2 ] W^{[2]} W[2]、 b [ 2 ] b^{[2]} b[2]的维度之后,接下来重点推导一下神经网络的正向传播过程。
6.2.1 网络输出
从输入层到隐藏层,h1、h2、h3、h4神经元计算分为线性部分和非线性部分,整个过程可以写成:
z 1 [ 1 ] = W 1 [ 1 ] x + b 1 [ 1 ] , a 1 [ 1 ] = g ( z 1 [ 1 ] ) z_1^{[1]}=W_1^{[1]}x+b_1^{[1]},\ \ a_1^{[1]}=g(z_1^{[1]}) z1[1]=W1[1]x+b1[1], a1[1]=g(z1[1])
z 2 [ 1 ] = W 2 [ 1 ] x + b 2 [ 1 ] , a 2 [ 1 ] = g ( z 2 [ 1 ] ) z_2^{[1]}=W_2^{[1]}x+b_2^{[1]},\ \ a_2^{[1]}=g(z_2^{[1]}) z2[1]=W2[1]x+b2[1], a2[1]=g(z2[1])
z 3 [ 1 ] = W 3 [ 1 ] x + b 3 [ 1 ] , a 3 [ 1 ] = g ( z 3 [ 1 ] ) z_3^{[1]}=W_3^{[1]}x+b_3^{[1]},\ \ a_3^{[1]}=g(z_3^{[1]}) z3[1]=W3[1]x+b3[1], a3[1]=g(z3[1])
z 4 [ 1 ] = W 4 [ 1 ] x + b 4 [ 1 ] , a 4 [ 1 ] = g ( z 4 [ 1 ] ) z_4^{[1]}=W_4^{[1]}x+b_4^{[1]},\ \ a_4^{[1]}=g(z_4^{[1]}) z4[1]=W4[1]x+b4[1], a4[1]=g(z4[1])
其中,下标表示第几个神经元。例如 z j [ l ] z_j^{[l]} zj[l]就表示第 l l l层的第 j j j个神经元。注意, j j j从1开始, l l l从0开始。 z j [ l ] z_j^{[l]} zj[l]是线性输出, a j [ l ] a_j^{[l]} aj[l]是非线性输出, g ( ⋅ ) g(\cdot) g(⋅)表示激活函数。关于激活函数,稍后详细介绍。
从隐藏层到输出层,只有一个out神经元。注意此时神经元的输入不是 x x x,而是隐藏层的输出 a [ 1 ] a^{[1]} a[1]。整个过程为:
z 1 [ 2 ] = W 1 [ 2 ] a [ 1 ] + b 1 [ 2 ] , a 1 [ 2 ] = g ( z 1 [ 2 ] ) z_1^{[2]}=W_1^{[2]}a^{[1]}+b_1^{[2]},\ \ a_1^{[2]}=g(z_1^{[2]}) z1[2]=W1[2]a[1]+b1[2], a1[2]=g(z1[2])
为了提高程序运算速度,我们利用之前介绍的向量化思想,将上述表达式转换成矩阵运算的形式:
z [ 1 ] = W [ 1 ] x + b [ 1 ] z^{[1]}=W^{[1]}x+b^{[1]} z[1]=W[1]x+b[1]
a [ 1 ] = g ( z [ 1 ] ) a^{[1]}=g(z^{[1]}) a[1]=g(z[1])
z [ 2 ] = W [ 2 ] a [ 1 ] + b [ 2 ] z^{[2]}=W^{[2]}a^{[1]}+b^{[2]} z[2]=W[2]a[1]+b[2]
a [ 2 ] = g ( z [ 2 ] ) a^{[2]}=g(z^{[2]}) a[2]=g(z[2])
以上介绍的是单个样本的正向传输过程,如果有m个样本,则输入X的维度为(3,m)。最简单的可以使用for循环来计算其正向输出。这里,我们用上标(i)表示第i个样本。过程如下:
for i=1 to m:
Z [ 1 ] ( i ) = W [ 1 ] X ( i ) + b [ 1 ] Z^{[1](i)}=W^{[1]}X^{(i)}+b^{[1]} Z[1](i)=W[1]X(i)+b[1]
A [ 1 ] ( i ) = g ( Z [ 1 ] ( i ) ) A^{[1](i)}=g(Z^{[1](i)}) A[1](i)=g(Z[1](i))
Z [ 2 ] ( i ) = W [ 2 ] A [ 1 ] ( i ) + b [ 2 ] Z^{[2](i)}=W^{[2]}A^{[1](i)}+b^{[2]} Z[2](i)=W[2]A[1](i)+b[2]
A [ 2 ] ( i ) = g ( Z [ 2 ] ( i ) ) A^{[2](i)}=g(Z^{[2](i)}) A[2](i)=g(Z[2](i))
这里,X、Z、A都采用大写的形式,表示矩阵。 Z [ 1 ] Z^{[1]} Z[1]和 A [ 1 ] A^{[1]} A[1]的维度为(4,m), Z [ 2 ] Z^{[2]} Z[2]和 A [ 2 ] A^{[2]} A[2]的维度为(1,m)。对这四个矩阵均可以这样理解:行表示第几个神经元,列表示样本数目m。
不使用for循环,直接采用矩阵运算的形式,可得:
Z [ 1 ] = W [ 1 ] X + b [ 1 ] Z^{[1]}=W^{[1]}X+b^{[1]} Z[1]=W[1]X+b[1]
A [ 1 ] = g ( Z [ 1 ] ) A^{[1]}=g(Z^{[1]}) A[1]=g(Z[1])
Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]} Z[2]=W[2]A[1]+b[2]
A [ 2 ] = g ( Z [ 2 ] ) A^{[2]}=g(Z^{[2]}) A[2]=g(Z[2])
这样,我们就完整地计算了神经网络模型的正向传播过程。有时候,为了便于理解, X X X也可以用 A [ 0 ] A^{[0]} A[0]表示。
6.2.2 激活函数
神经网络每个神经元都需要激活函数(Activation Function)来进行非线性运算。在上一篇中介绍的逻辑回归模型使用的Sigmoid函数,也是一种激活函数。下面重点介绍几个神经网络常用的激活函数 g ( x ) g(x) g(x),并作简单比较。
(1)Sigmoid函数

函数表达式为:
a = 1 1 + e − z a=\frac{1}{1+e^{-z}} a=1+e−z1
(2)tanh函数

函数表达式为:
a = e z − e − z e z + e − z a=\frac{e^z-e^{-z}}{e^z+e^{-z}} a=ez+e−zez−e−z
(3)ReLU函数

函数表达式为:
a = m a x ( 0 , z ) a = max(0,z) a=max(0,z)
(4)Leaky ReLU函数
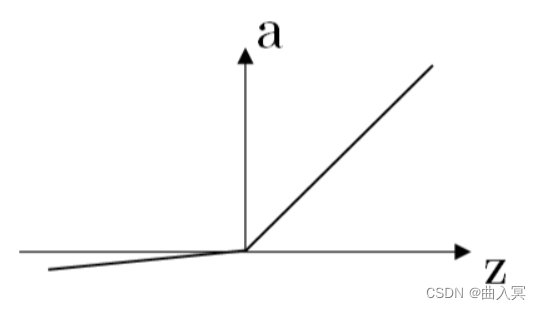
函数表达式为:
a = { λ z , z ⩽ 0 z , z > 0 a=\left\{\begin{array}{cc} \lambda z, & z\leqslant0\\ z, & z> 0 \end{array}\right. a={λz,z,z⩽0z>0
其中, λ \lambda λ为可变参数,一般 λ ∈ ( 0 , 1 ) \lambda\in(0,1) λ∈(0,1),例如 λ = 0.01 \lambda=0.01 λ=0.01。
介绍完了这些常用的激活函数之后,考虑如何选择合适的激活函数呢?首先我们来比较Sigmoid函数和tanh函数。对于隐藏层的激活函数,一般来说,tanh函数要比Sigmoid函数表现更好一些。因为tanh函数的取值范围在(-1,+1),即隐藏层的输出被限定在(-1,+1)之间,可以看成是在0值附近分布,均值为0。这样从隐藏层到输出层,数据起到了归一化(均值为0)的效果。因此,隐藏层的激活函数,tanh比Sigmoid更好一些。而对于输出层的激活函数,因为二分类问题的输出取值为[0, 1]之间,所以一般会选择Sigmoid作为激活函数。
观察Sigmoid函数和tanh函数,我们发现有这样一个问题,就是当 ∣ z ∣ |z| ∣z∣很大的时候,激活函数的斜率(梯度)很小。因此,在这个区域内,梯度下降算法会运行得比较慢。在实际应用中,应尽量避免使z落在这个区域,使 ∣ z ∣ |z| ∣z∣尽可能限定在零值附近,从而提高梯度下降算法运算速度。
为了弥补Sigmoid函数和tanh函数的这个缺陷,就出现了ReLU激活函数。ReLU激活函数在 z z z大于零时梯度始终为1;在 z z z小于零时梯度始终为0; z z z等于零时的梯度可以当成1也可以当成0,实际应用中并不影响。对于隐藏层,选择ReLU作为激活函数能够保证 z z z大于零时梯度始终为1,从而提高神经网络梯度下降算法运算速度。但当 z z z小于零时,存在梯度为0的缺点。实际应用中,这个缺点影响不是很大,但为了弥补这个缺点,出现了Leaky ReLU激活函数,能够保证 z z z小于零时梯度不为0。
值得注意的是,如果是二分类问题,输出层可以使用Sigmoid激活函数。如果是预测问题,输出层则可以不需要使用激活函数,因为预测值一般在整个实数范围之间。又或者,如果输出值总是正数,例如房价预测问题,则可以使用ReLU激活函数。
因此,是否使用激活函数,使用哪个激活函数,并不是固定不变的,需要根据问题本身进行考量和判断,做到活学活用,真正理解。本文为了简化内容,仅仅以二分类为例,介绍神经网络的基本模型。更复杂的情况,后面的章节将会详细介绍。
有的人可能会有疑问:为什么每个神经元需要非线性单元,需要激活函数?以上面这个神经网络模型为例,我们来看如果没有激活函数,模型最后的输出是什么。
假设没有激活函数,则有 A = Z A = Z A=Z。那么,神经网络的各层输出为:
Z [ 1 ] = W [ 1 ] X + b [ 1 ] Z^{[1]}=W^{[1]}X+b^{[1]} Z[1]=W[1]X+b[1]
A [ 1 ] = Z [ 1 ] A^{[1]}=Z^{[1]} A[1]=Z[1]
Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]} Z[2]=W[2]A[1]+b[2]
A [ 2 ] = Z [ 2 ] A^{[2]}=Z^{[2]} A[2]=Z[2]
直接对 A [ 2 ] A^{[2]} A[2]表达式展开:
A [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] = W [ 2 ] ( W [ 1 ] X + b [ 1 ] ) + b [ 2 ] = ( W [ 2 ] W [ 1 ] X ) + ( W [ 2 ] b [ 1 ] + b [ 2 ] ) = W ′ X + b ′ A^{[2]}=W^{[2]}A^{[1]}+b^{[2]}=W^{[2]}(W^{[1]}X+b^{[1]})+b^{[2]}\\=(W^{[2]}W^{[1]}X)+(W^{[2]}b^{[1]}+b^{[2]})=W'X+b' A[2]=W[2]A[1]+b[2]=W[2](W[1]X+b[1])+b[2]=(W[2]W[1]X)+(W[2]b[1]+b[2])=W′X+b′
经过推导,发现 A [ 2 ] A^{[2]} A[2]仍是输入变量 X X X的线性组合。这表明,使用神经网络与直接使用线性模型的效果并没有什么两样。即便是包含多层隐藏层的神经网络,如果不使用非线性激活函数,最终的输出仍然是输入 X X X的线性模型。这样的话神经网络就没有任何作用了。另外,如果只有输出层使用非线性激活函数,那么整个神经网络的结构就类似于一个简单的逻辑回归模型,而失去了神经网络模型本身的优势和价值。因此,隐藏层一般必须使用非线性激活函数。
6.3 神经网络反向传播
神经网络正向传播最终得到的输出 Y ^ = A [ 2 ] \hat Y=A^{[2]} Y^=A[2]。因为是二分类问题,其损失函数与逻辑回归模型一样,在上一篇已经推导过逻辑回归模型的损失函数:
L = − [ y l o g y ^ + ( 1 − y ) l o g ( 1 − y ^ ) ] L=-[ylog\hat y+(1-y)log(1-\hat y)] L=−[ylogy^+(1−y)log(1−y^)]
对于 m m m个样本的损失函数为:
J = − 1 m ∑ i = 1 m y ( i ) l o g y ^ ( i ) + ( 1 − y ( i ) ) l o g ( 1 − y ^ ( i ) ) J=-\frac{1}{m}\sum_{i=1}^my^{(i)}log\hat y^{(i)}+(1-y^{(i)})log(1-\hat y^{(i)}) J=−m1i=1∑my(i)logy^(i)+(1−y(i))log(1−y^(i))
接下来,我们来计算损失函数 J J J对各个变量 A [ 2 ] A^{[2]} A[2], Z [ 2 ] Z^{[2]} Z[2], W [ 2 ] W^{[2]} W[2], b [ 2 ] b^{[2]} b[2], A [ 1 ] A^{[1]} A[1], Z [ 1 ] Z^{[1]} Z[1], W [ 1 ] W^{[1]} W[1], b [ 1 ] b^{[1]} b[1]的偏导数。
J J J对 A [ 2 ] A^{[2]} A[2]求偏导数:
d A [ 2 ] = ∂ J ∂ A [ 2 ] = A [ 2 ] − Y A [ 2 ] ( 1 − A [ 2 ] ) dA^{[2]}=\frac{\partial J}{\partial A^{[2]}}=\frac{A^{[2]}-Y}{A^{[2]}(1-A^{[2]})} dA[2]=∂A[2]∂J=A[2](1−A[2])A[2]−Y
J J J对 Z [ 2 ] Z^{[2]} Z[2]求偏导数:
d Z [ 2 ] = d A [ 2 ] ⋅ ∂ A [ 2 ] ∂ Z [ 2 ] dZ^{[2]}=dA^{[2]}\cdot\frac{\partial A^{[2]}}{\partial Z^{[2]}} dZ[2]=dA[2]⋅∂Z[2]∂A[2]
这里,若使用Sigmoid激活函数,它的导数为:
g ( z ) ′ = a ( 1 − a ) g(z)'=a(1-a) g(z)′=a(1−a)
则有:
∂ A [ 2 ] ∂ Z [ 2 ] = A [ 2 ] ( 1 − A [ 2 ] ) \frac{\partial A^{[2]}}{\partial Z^{[2]}}=A^{[2]}(1-A^{[2]}) ∂Z[2]∂A[2]=A[2](1−A[2])
将其带入 d Z [ 2 ] dZ^{[2]} dZ[2]中,得:
d Z [ 2 ] = A [ 2 ] − Y A [ 2 ] ( 1 − A [ 2 ] ) ⋅ A [ 2 ] ( 1 − A [ 2 ] ) = A [ 2 ] − Y dZ^{[2]}=\frac{A^{[2]}-Y}{A^{[2]}(1-A^{[2]})}\cdot A^{[2]}(1-A^{[2]})=A^{[2]}-Y dZ[2]=A[2](1−A[2])A[2]−Y⋅A[2](1−A[2])=A[2]−Y
发现 d Z [ 2 ] dZ^{[2]} dZ[2]的表达式是不是很简单呢?
J 对 W [ 2 ] J对W^{[2]} J对W[2]求偏导数:
d W [ 2 ] = 1 m d Z [ 2 ] ⋅ ∂ Z [ 2 ] ∂ W [ 2 ] = 1 m d Z [ 2 ] ⋅ A [ 1 ] T dW^{[2]}=\frac1m dZ^{[2]}\cdot\frac{\partial Z^{[2]}}{\partial W^{[2]}}=\frac1m dZ^{[2]}\cdot A^{[1]T} dW[2]=m1dZ[2]⋅∂W[2]∂Z[2]=m1dZ[2]⋅A[1]T
其中, A [ 1 ] T A^{[1]T} A[1]T表示 A [ 1 ] A^{[1]} A[1]的转置。
J 对 b [ 2 ] J对b^{[2]} J对b[2] 求偏导数:
d b [ 2 ] = 1 m n p . s u m ( d Z [ 2 ] , a x i s = 1 ) db^{[2]}=\frac1mnp.sum(dZ^{[2]},\ \ axis=1) db[2]=m1np.sum(dZ[2], axis=1)
这里的np.sum()是Python Numpy中的求和函数,参数axis = 0表示矩阵行相加,axis = 1表示矩阵列相加。
J J J对 A [ 1 ] A^{[1]} A[1]求偏导数:
d A [ 1 ] = d Z [ 2 ] ⋅ ∂ Z [ 2 ] ∂ A [ 1 ] = W [ 2 ] T ⋅ d Z [ 2 ] dA^{[1]}=dZ^{[2]}\cdot\frac{\partial Z^{[2]}}{\partial A^{[1]}}=W^{[2]T}\cdot dZ^{[2]} dA[1]=dZ[2]⋅∂A[1]∂Z[2]=W[2]T⋅dZ[2]
J 对 Z [ 1 ] J对Z^{[1]} J对Z[1]求偏导数:
d Z [ 1 ] = d A [ 1 ] ⋅ ∂ A [ 1 ] ∂ Z [ 1 ] = d A [ 1 ] ∗ g [ 1 ] ′ ( Z [ 1 ] ) = W [ 2 ] T ⋅ d Z [ 2 ] ∗ g [ 1 ] ′ ( Z [ 1 ] ) dZ^{[1]}=dA^{[1]}\cdot\frac{\partial A^{[1]}}{\partial Z^{[1]}}=dA^{[1]}*g^{[1]'}(Z^{[1]})=W^{[2]T}\cdot dZ^{[2]}*g^{[1]'}(Z^{[1]}) dZ[1]=dA[1]⋅∂Z[1]∂A[1]=dA[1]∗g[1]′(Z[1])=W[2]T⋅dZ[2]∗g[1]′(Z[1])
其中, g [ 1 ] ′ ( Z [ 1 ] ) g^{[1]'}(Z^{[1]}) g[1]′(Z[1])表示 A [ 1 ] A^{[1]} A[1]对 Z [ 1 ] Z^{[1]} Z[1]的导数。上式中的*号表示两个矩阵对应元素相乘, ⋅ \cdot ⋅表示矩阵相乘。
J J J对 W [ 1 ] W^{[1]} W[1]求偏导数:
d W [ 1 ] = d Z [ 1 ] ⋅ ∂ Z [ 1 ] ∂ W [ 1 ] = 1 m d Z [ 1 ] ⋅ A [ 0 ] T dW^{[1]}=dZ^{[1]}\cdot\frac{\partial Z^{[1]}}{\partial W^{[1]}}=\frac1mdZ^{[1]}\cdot A^{[0]T} dW[1]=dZ[1]⋅∂W[1]∂Z[1]=m1dZ[1]⋅A[0]T
J J J对 b [ 1 ] b^{[1]} b[1]求偏导数:
d b [ 1 ] = 1 m n p . s u m ( d Z [ 1 ] , a x i s = 1 ) db^{[1]}=\frac1mnp.sum(dZ^{[1]},\ \ axis=1) db[1]=m1np.sum(dZ[1], axis=1)
好了,我们已经完整地推导了神经网络反向传播过程。
我把正向传播和反向传播涉及的公式全都整理出来,以供查阅:

计算完 W W W和 b b b的导数之后,利用上一篇介绍过的梯度下降算法,更新 W W W和 b b b:
W [ 1 ] = W [ 1 ] − η ⋅ d W [ 1 ] W^{[1]}=W^{[1]}-\eta\cdot dW^{[1]} W[1]=W[1]−η⋅dW[1]
b [ 1 ] = b [ 1 ] − η ⋅ d b [ 1 ] b^{[1]}=b^{[1]}-\eta\cdot db^{[1]} b[1]=b[1]−η⋅db[1]
W [ 2 ] = W [ 2 ] − η ⋅ d W [ 2 ] W^{[2]}=W^{[2]}-\eta\cdot dW^{[2]} W[2]=W[2]−η⋅dW[2]
b [ 2 ] = b [ 2 ] − η ⋅ d b [ 2 ] b^{[2]}=b^{[2]}-\eta\cdot db^{[2]} b[2]=b[2]−η⋅db[2]
其中, η \eta η是学习因子。
6.4 W和b的初始化
神经网络模型在开始训练时需要对各层权重系数 W W W和常数项 b b b进行初始化赋值。初始化赋值时, b b b一般全部初始化为0即可,但是 W W W不能全部初始化为0。接下来我们来分析一下原因。
还是上面的神经网络模型,如果 W [ 1 ] W^{[1]} W[1]和 W [ 2 ] W^{[2]} W[2]全部初始化为0,即:
W [ 1 ] = [ 0 0 0 0 0 0 0 0 0 0 0 0 ] W^{[1]}= \left[ \begin{matrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{matrix} \right] W[1]= 000000000000
W [ 2 ] = [ 0 0 0 0 ] W^{[2]}= \left[ \begin{matrix} 0 & 0 & 0 & 0 \end{matrix} \right] W[2]=[0000]
这样使得隐藏层四个神经元的输出都相同,即:
A 1 [ 1 ] = A 2 [ 1 ] = A 3 [ 1 ] = A 4 [ 1 ] A_1^{[1]}=A_2^{[1]}=A_3^{[1]}=A_4^{[1]} A1[1]=A2[1]=A3[1]=A4[1]
经过推导得到:
d Z 1 [ 1 ] = d Z 2 [ 1 ] = d Z 3 [ 1 ] = d Z 4 [ 1 ] dZ_1^{[1]}=dZ_2^{[1]}=dZ_3^{[1]}=dZ_4^{[1]} dZ1[1]=dZ2[1]=dZ3[1]=dZ4[1]
以及:
d W 1 [ 1 ] = d W 2 [ 1 ] = d W 3 [ 1 ] = d W 4 [ 1 ] dW_1^{[1]}=dW_2^{[1]}=dW_3^{[1]}=dW_4^{[1]} dW1[1]=dW2[1]=dW3[1]=dW4[1]
因此,隐藏层四个神经元对应的权重行向量 W 1 [ 1 ] W_1^{[1]} W1[1]、 W 2 [ 1 ] W_2^{[1]} W2[1]、 W 3 [ 1 ] W_3^{[1]} W3[1]、 W 4 [ 1 ] W_4^{[1]} W4[1]每次迭代更新都会得到完全相同的结果。也就是说,始终有:
W 1 [ 1 ] = W 2 [ 1 ] = W 3 [ 1 ] = W 4 [ 1 ] W_1^{[1]}=W_2^{[1]}=W_3^{[1]}=W_4^{[1]} W1[1]=W2[1]=W3[1]=W4[1]
这样隐藏层设置多个神经元就没有任何意义了。
所以,一般对 W W W进行随机初始化。相应的Python语句为:
W1 = np.random.randn((4,3))*0.01
b1 = np.zero((4,1))
W2 = np.random.randn((1,4))*0.01
b2 = 0
值得注意的是,W1和W2都习惯性地乘以0.01。究其原因,是因为如果使用Sigmoid或者tanh作为激活函数的话, W W W比较小,得到的 ∣ Z ∣ |Z| ∣Z∣也比较小(零点附近),而零点附近区域的梯度比较大,这样能大大提高梯度下降算法的更新速度,尽快找到全局最优解。如果 W W W较大,得到的 ∣ Z ∣ |Z| ∣Z∣也比较大,接近曲线平缓区域,梯度很小,更新速度慢,训练过程也会慢很多。当然,如果使用ReLU或者Leaky ReLU,则可以不乘以0.01。
6.5 总结
本文主要介绍了最简单的2层神经网络模型,详细推导其正向传播过程和反向传播过程,得到了各权重系数W和常数项b的导数表达式。我们也列举了常见的四种激活函数,分析各自的优缺点。最后,简单解释了参数初始化的方法和注意事项。
这篇关于深度学习——第6章 浅层神经网络(NN)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




