计算机图形学实验二-实现圆的中点算法、椭圆的中点算法

1、圆的中点算法说明

算法说明：

（1）圆的中点算法主要思想是将绘图区域分成八个部分，利用圆的对称性，只要画出一个部分的弧线即可将整个圆形绘出，这里借用老师上课ppt中的一个图片，如下图所示，白色区域的点针对其他七个部分都有对称的点的坐标，所以利用圆的8对称性，只须讨论1/8圆：第一象限内x∈[0,R/2^(1/2)]的1/8圆弧即可。

1. 下面对绘制白色区域的弧线的算法进行说明，构造函数：F（X，Y）=X2  +  Y2 -  R2，则F(X，Y)= 0：（X，Y）在圆周上；F(X，Y)< 0：（X，Y）在圆内；F(X，Y)> 0：（X，Y）在圆外。如果dM<0，表示下一中点M在圆内，选择T点，∆dMT= dMT - dM=2xp+3；如果dM>0，表示下一中点M在圆外，选择B点，且：∆dMB= dMB - dM=2xp-2yp +5 ，d的初值是dM0=1.25-R，为了优化算法，这里将dM0=1-R，判断其是否小于0即可。

算法实现及测试：

从上图可以看出我在初始化画布之前有具体算法的选择，后面的两个后续讲解，选择绘制圆形之后，可以由用户自定义圆的半径，由于我这里给出的画布大小是400×400的，所以为了避免圆无法完整显示的情况，输出提示信息提示用户输入圆的半径的范围。

1. 椭圆的中点算法说明

算法说明：椭圆跟圆形有相似之处也有不同之处，圆形是八对称性，而椭圆是四对称性，所以这里只考虑第一象限的弧线绘制即可。设出椭圆的隐函数方程F(x,y)之后进行判断，F(X,Y) = 0 ：(X,Y) 在椭圆上；F(X,Y) < 0 ：(X,Y) 在椭圆内；F(X,Y) > 0 ：(X,Y) 在椭圆外，这里还有一个特别注意的点，椭圆有上下两部分，而划分依据是(b^2)*x≥(a^2)*y与否，所以针对两个不同的部分，适时调整xy坐标，即当(b^2)*x≥(a^2)*y的时候，进行x坐标和y坐标的交换，这样就可继续使用设计的算法，原来的算法不会有太大的改动。

算法的实现和测试：

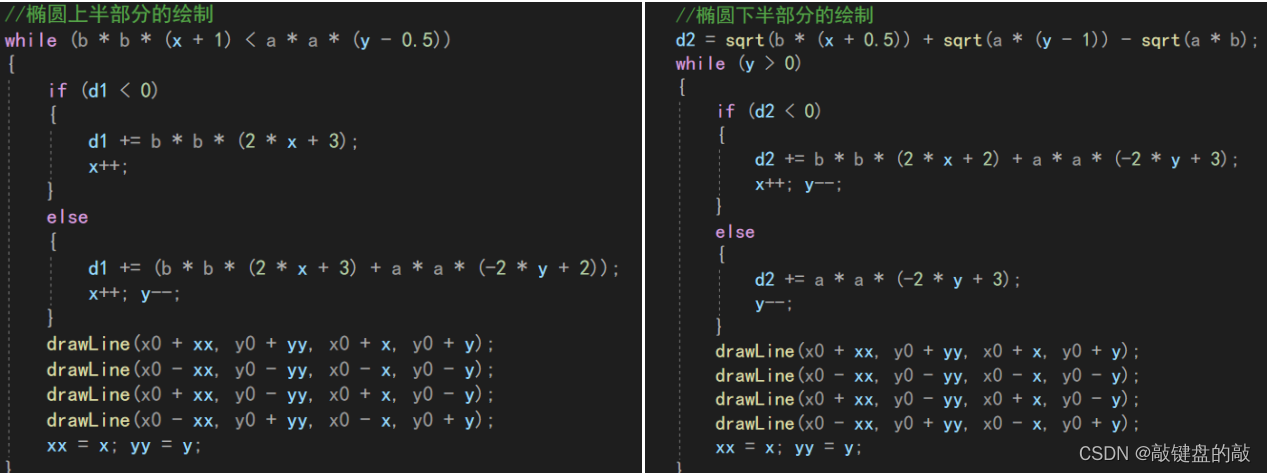
左图是椭圆上半部分的绘制，右图是椭圆下半部分的绘制，drawLine函数是绘制对应四个象限的弧线，针对不同的d1/d2，进行不同的x坐标和y坐标的增量。

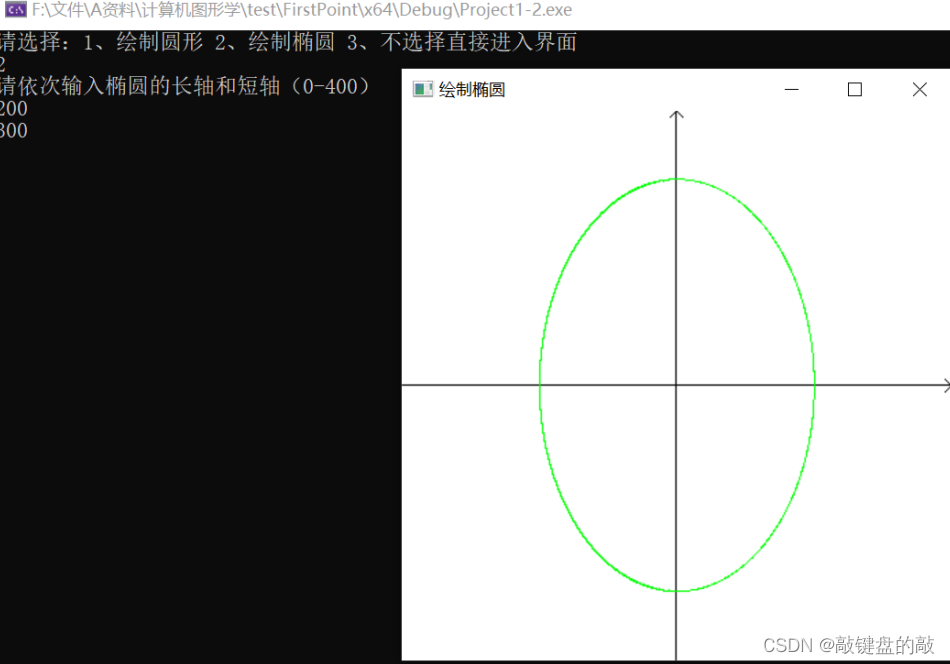
上图即为算法测试结果，同样先由用户选择绘制椭圆算法，然后依次输入椭圆的长轴和短轴长度，同时这里为了避免绘制图形出界问题规定了长轴和短轴的范围。

1. 鼠标的交互

前面两种算法的实现是基于用户在控制台的输入（圆的半径或者椭圆的长短轴），在实现两种算法的同时，我加入了鼠标的交互，即用户选择3（或者输入非1、2的字符），直接进入空白页面，鼠标右键点击弹出选择菜单，选择Circle是绘制圆形，选择Oval是绘制椭圆，即用户可以在进入画布之后，自由选择圆或者椭圆的绘制。

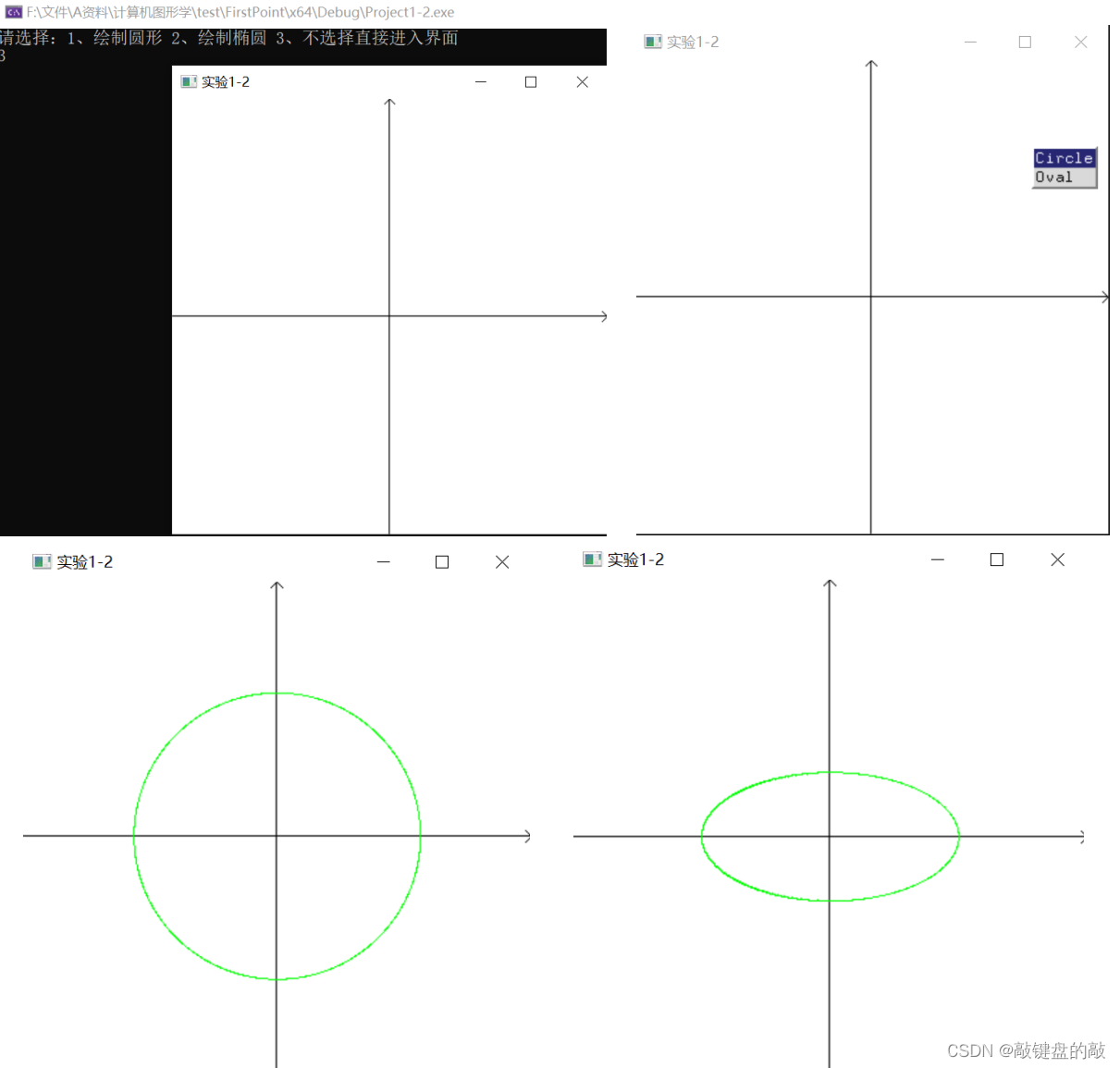
3.2 实验总结和收获

本次实验是利用中点画线算法实现圆和椭圆的绘制，在实现基本的绘制之后，我加入了用户自定义选择选项和由用户自定义圆的半径和椭圆的长短轴选择，此外，若用户不想输入操作，则直接进入画布，在画布中点击鼠标右键即可自由选择绘制圆形或者椭圆形。这里我分析了两者的优缺点，前者优点是用户可以自己选择绘制的圆和椭圆的大小，缺点是需要用户输入数据之后才能看到图形绘制出来的样子并且用户启动一次程序，只能选择绘制圆形或者椭圆形，过程不可逆；后者优点是用户进入画布后可以重复性自由选择绘制圆形还是椭圆形，启动一次程序即可，缺点是不能自由设定圆形或者椭圆形的大小。

详细代码见链接：https://download.csdn.net/download/weixin_53249260/88218026