先手和后手零和博弈拿值，请问谁最后得分高，得多少分

先手和后手零和博弈拿值，请问谁最后得分高？得多少分？

提示：DP2：从L--R范围上的尝试模型

文章目录

• 先手和后手零和博弈拿值，请问谁最后得分高？得多少分？
• • @[TOC](文章目录)
• 题目
• 一、审题
• 二、解题
• 根据暴力递归改动态规划填表的代码
• 还有一种暴力递归改动态规划的填表方法，斜着来
• 总结

题目

先手，和后手，
先手先在数组arr上拿值，可以从左边拿，也可以从右边拿
但是先手后手是零和博弈，也就是，任何人，我目前拿一个值，有利于我自己得分高，同时也要想办法让对手下次拿的得分低。
请问，先手后手谁拿的分高？最高是多少？

一、审题

示例1：
arr= 3 100 7 10
（1）先手先拿，不管如何，先手要拿一个对自己有利的，但是也让对收下次拿尽量少，所以先手不能拿3，因为对手下次能拿100，于是先手选择拿10
arr=3 100 7
（2）后手拿，后手也要拿一个更大的值，但是希望对手不要拿到更好的，没什么办法，后手只能拿7
arr=3 100
（3）先手拿，先手要拿更大的，让对手拿一个最小的，拿走100
arr=3
（4）后手拿，就一个值，自己拿了3
所以先手赢了，综合10+100=110

示例2：
arr= 3 100 7
（1）先手先拿，不管如何，先手要拿一个对自己有利的，但是也让对收下次拿尽量少，所以先手不能拿3，选择拿10
arr= 3 100
（2）后手拿，拿更大的，让对手拿小的，拿走100
arr=3
（3）先手拿，就一个值，自己拿了3
所以后手赢了，综合100

二、解题

涉及到零和博弈：
从arr的0–N-1范围上，先手拿
从arr的0–N-1范围上，后手拿
轮番拿，看谁的得分更大？

事情是这样的，先手拿完一个值，可以选arr中的L，或者R，我希望拿最大值，然后先手立马就变后手了，
变后手了以后，只能拿最小的【因为零和博弈，对手绝对不会给我留大的数！】

所以，我们定义一个函数，f(arr,L,R) 是先手从L–R范围内拿，拿到的最大得分。
（1）那么我们f(arr,L,R)内部咋处理呢？
——如果L=R，则就一个数，先手直接拿了，返回arr[L]
刚刚说了，先手自由选L或者R，然后作为后手去拿剩下的部分；
——不妨设我先手先拿了L，此后就只能以后手的身份去L+1–R上拿了。得分是p1 = arr[L]+second(arr,L+1,R)

——不妨设，先手先拿了R，则此后，先手只能以后手的身份去拿L–R-1了，得分是p2 = arr[R]+second(arr,L,R-1)

究竟先手拿左边更好呢？还是拿右边更好呢？
很简单，选max（p1，p2）返回即可；

对于后手呢？后手从L–R上拿，自己的最大得分是多少？
（2）定义为：second(arr,L,R)
——如果L=R，则就一个数，先手肯定直接拿了，既然我此刻是后手，那很不好意思，我没有啥可以拿，得分为0；惨
——如果先手拿了L，那我现在的身份就是先手了，但是我的对手（先手），刚刚绝不会给我留下好结果的，所以我只能拿差的结果，
但不管如何，我此刻以先手的身份去拿，尽量还是拿一个最好的值：s1 = f(arr,L+1,R）

——如果先手拿走了R，那后手此刻以先手的身份去拿L–R-1上的，尽量拿对我后手更好的结果：s2=f(arr,L,R-1)

只不过，不管人先手曾经拿了L还是拿了R，我后手，现在以先手的身份拿，绝对只能拿到刚刚先手留给我的最差结果，因为规则就是零和博弈！！！
于是我后手拿最好的结果，其实也是先手留给我的最差结果，返回：
min（s1，s2）；

看见了没？
先手返回就是max（p1，p2），而后手就是min（s1，s2）
为啥呢？先手先拿，当然拿走最好的，但是这个先手留给后手的结果只能是最差的，这就是零和博弈的本质！所以
即使后手拿的时候，以先手的身份拿，但是后手就是拿最小值，因为先手不会给后手留好的结果。
——一定要把这个逻辑捋清楚，先手先拿，必定拿最好，留给后手的结果必定最差。——零和博弈

好，知道了这个情况，咱们就可以撸代码了
（1）先手先拿得分的代码：

//复习：//我们定义一个函数，**f(arr,L,R)**是先手从L--R范围内拿，拿到的最大得分。public static int f(int[] arr, int L, int R){//（1）那么我们f(arr,L,R)内部咋处理呢？//——如果L=R，则就一个数，先手直接拿了，返回arr[L]if (L == R) return arr[L];//刚刚说了，先手自由选L或者R，然后作为后手去拿剩下的部分；//——不妨设我先手先拿了L，此后就只能以后手的身份去L+1--R上拿了。得分是p1 = arr[L]+**second(arr,L+1,R)**int p1 = arr[L] + g(arr, L + 1, R);//——不妨设，先手先拿了R，则此后，先手只能以后手的身份去拿L--R-1了，得分是p2 = arr[R]+**second(arr,L,R-1)**int p2 = arr[R] + g(arr, L, R - 1);//究竟先手拿左边更好呢？还是拿右边更好呢？//很简单，选**max**（p1，p2）返回即可；return Math.max(p1, p2);}

（2）后手后拿得分的代码：

//（2）定义为：**second(arr,L,R)**public static int g(int[] arr, int L, int R) {//——如果L=R，则就一个数，先手肯定直接拿了，既然我此刻是后手，那很不好意思，我没有啥可以拿，得分为0；惨if (L == R) return 0;//——如果先手拿了L，那我现在的身份就是先手了，但是我的对手（先手），刚刚绝不会给我留下好结果的，所以我只能拿差的结果，//但不管如何，我此刻以先手的身份去拿，尽量还是拿一个最好的值：**s1 = f(arr,L+1,R）**int s1 = f(arr,L + 1, R);//——如果先手拿走了R，那后手此刻以先手的身份去拿L--R-1上的，尽量拿对我后手更好的结果：**s2=f(arr,L,R-1)**int s2 = f(arr, L, R - 1);//只不过，不管人先手曾经拿了L还是拿了R，我后手，现在以先手的身份拿，**绝对只能拿到刚刚先手留给我的最差结果**，因为规则就是零和博弈！！！//于是我后手拿最好的结果，其实也是先手留给我的最差结果，返回：**min**（s1，s2）；return Math.min(s2, s1);}

OK，任意数组，就像案例1和案例2，可能先手还会输呢？究竟鹿死谁手？
咱们这样做，直接对比先手拿，和后手拿，看看谁更大就得了呗。

//主函数调用public static int maxScore(int[] arr){if (arr == null || arr.length == 0) return 0;int N = arr.length;//左边先手拿，后边后手拿，反正都是arr整体范围上去拿就行，看看谁赢？return Math.max(f(arr, 0, N - 1), g(arr, 0,  N - 1));}

用案例测试一把：

数组1：
3 100 7 10 
110数组2：
3 100 7 
100

是不是很完美？

根据暴力递归改动态规划填表的代码

上面的暴力递归，2个函数f和g，每个函数都是有L和R俩变量，自然需要填2个表，都是2维的信息表

针对这个题，先手和后手都是L–R范围上去拿，这种动态规划的类型是从L–R范围上的尝试模型
有固定的的填表套路的，正常情况下L<=R，L>R是不可能的

比如，针对先手得分的暴力递归函数：f(int[] arr, int L, int R)
L和R都可以取0–N-1范围
则就是一个二维表dpf，每个格子dpf[L][R]:代表每一种L和R取值下，先手从L–R范围上拿值，得到的最大得分是多少？
（0）看图中五角星那个格子，dpf[0][N-1]=f(arr,0, N-1)就代表我们要的结果，先手从0–N-1范围上拿值，最大得分是？
（1）当L>R不可能，所以表格的左下角部分，都不用填哦！！！
（2）当L=R就是表中的主对角线，自然dpf[L][R] = arr[L]，这是根据暴力递归中的代码来改的
（3）当R=L+1就是表中的副对角线，自然看L和R谁大，取谁，dpf[L][R] = max(arr[L],arr[R])，你想想是不是，就俩值，先手肯定拿走最大的呗。

（4）任意位置dpf[L][R] 怎么填？
咱们从最后N-2那行开始，每次从表格中蓝色圈1开始填，然后一行一行往上推，
行起点是L=N-3行一直到0行，列起点R=N-1列即R就是L+2，一直到N-1列；这样按顺序填表
咋填一会说

先看后手的表格怎么填写？
针对后手得分的暴力递归函数：g(int[] arr, int L, int R)
L和R都可以取0–N-1范围
则就是一个二维表dps，每个格子dps[L][R]:代表每一种L和R取值下，后手从L–R范围上拿值，得到的最大得分是多少？
由于是后手，肯定不会得到啥好结果的
（2-0）看图中五角星那个格子，dps[0][N-1]=g(arr,0, N-1)就代表我们要的结果，后手从0–N-1范围上拿值，最大得分是？
（2-1）当L>R不可能，所以表格的左下角部分，都不用填哦！！！
（2-2）当L=R就是表中的主对角线，自然dps[L][R] = 0，这是根据暴力递归中的代码来改的，先手拿走了，后手没得拿，惨！
（2-3）当R=L+1就是表中的副对角线，自然看L和R谁小，取谁，dps[L][R] = min(arr[L],arr[R])，你想想是不是，就俩值，先手肯定拿走最大的呗，后手只能拿最小的！

（2-4）任意位置dps[L][R] 怎么填？
咱们从最后N-2那行开始，每次从表格中蓝色圈1开始填，然后一行一行往上推，
行起点是L=N-3行一直到0行，列起点R=N-1列即R就是L+2，一直到N-1列；这样按顺序填表

发现了吗？这个填表顺序竟然和先手一样的顺序
而且，先手暴力递归代码中，有这些：

int p1 = arr[L] + g(arr, L + 1, R);
int p2 = arr[R] + g(arr, L, R - 1);

转化为dpf格子就是这样的

int p1 = arr[L] + dps[L + 1][R];
int p2 = arr[R] + dps[L][R - 1];

先手的格子，依赖后手的格子dps！！！
同样，后手的格子依赖先手的格子dpf！！！
后手暴力递归的代码中有这俩：

int s1 = f(arr,L + 1, R);
int s2 = f(arr, L, R - 1);

转化为填表的格子是这样的

int s1 = dpf[L + 1][R];
int s2 = dpf[L][R - 1];

相互依赖，那咱们用在同一个宏观调度下，填上面蓝色圈1–圈6中

//然后倒回来填表--固定模式
咱们从最后N-2那行开始，每次从表格中蓝色圈1开始填，然后一行一行往上推，
行起点是L=N-3行一直到0行，列起点R=N-1列即R就是L+2，一直到N-1列；这样按顺序填表for (int i = N - 2; i >= 0; i--) {for (int j = i + 2; j < N; j++) {在这里面去填写剩下的格子，按照顺序

整体我们决定谁回赢呢？？
那就要看两个表中五角星那个格子，谁更大？
下面的i=L， j=R，不必疑惑！

//复习：根据暴力递归改动态规划填表的代码public static int getMaxValue3DP(int[] arr){if (arr == null || arr.length == 0) return 0;int N = arr.length;int[][] dpf = new int[N][N];//造表--默认全0int[][] dps = new int[N][N];//造表--默认全0//根据终止条件，填写对角线for (int i = 0; i < N; i++) {dpf[i][i] = arr[i];//s表，全0}//填写副对角for (int i = 0; i <= N - 2; i++) {//i控制行dpf[i][i + 1] = Math.max(arr[i], arr[i + 1]);dps[i][i + 1] = Math.min(arr[i], arr[i + 1]);}//然后倒回来填表--固定模式for (int i = N - 2; i >= 0; i--) {for (int j = i + 2; j < N; j++) {//咱们从最后N-2那行开始，每次从表格中蓝色圈1开始填，然后一行一行往上推，//行起点是L=N-3行一直到0行，列起点R=N-1列即R就是L+2，一直到N-1列；这样按顺序填表//根据暴力递归来--先手先拿//拿左边int p1 = arr[i] + dps[i + 1][j];//拿右边int p2 = arr[j] + dps[i][j - 1];//是更大，先手要谁？dpf[i][j] = Math.max(p1, p2);//我一定拿最好的//然后才能轮到后手拿——自然拿最差的结果，零和博弈//如果先手拿走了Lint p3 = dpf[i + 1][j];//如果先手拿走了Rint p4 = dpf[i][j - 1];//咋赵我都只能拿最次的dps[i][j] = Math.min(p3, p4);}}//先手后手都拿自己的五角星那个格子，对比谁大，谁赢了。return Math.max(dpf[0][N - 1], dps[0][N - 1]);//最终返回的最值}public static void test2(){int[] arr = {3, 100, 7, 10};int[] arr2 = {3, 100, 7};System.out.println("\n数组1：");for(Integer i : arr) System.out.print(i +" ");System.out.println();System.out.println(getMaxValue3DP(arr));System.out.println("\n数组2：");for(Integer i : arr2) System.out.print(i +" ");System.out.println();System.out.println(getMaxValue3DP(arr2));}public static void main(String[] args) {
//        test();test2();}

结果：

数组1：
3 100 7 10 
110数组2：
3 100 7 
100

你就说牛不牛吧！！！
这个题目，先手后手谁赢的动态规划代码，无非就是填写两个表格，而且俩表填写的时候，相互依赖的！
根据宏观调度，我们最后一个填写五角星那个格子，比较谁大，谁就行了。

还有一种暴力递归改动态规划的填表方法，斜着来

上面一节，咱们讲的是非常标准的一种动态规划填表法，你见了一定要学会

下面这种可以了解，但是很有趣，咱们啊，不用从蓝色圈1–6填
咱们愣是给他斜着填也行呀
只不过i和j要同时++

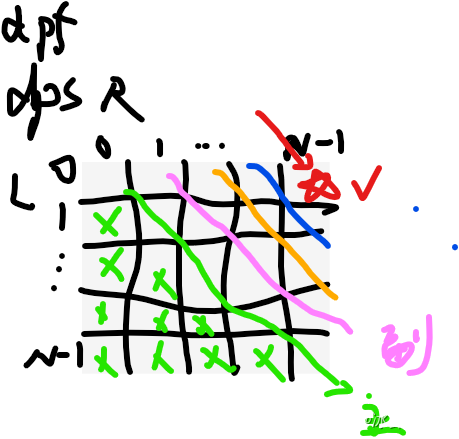
（1）最开始，咱们只填写主对角线，即可

//根据终止条件，填写对角线for (int i = 0; i < N; i++) {f[i][i] = arr[i];//s表，全0}

（2）然后从粉色，橘色，蓝色，红色依次斜着填表！
行从1行到N-1行，列的话，从j=1–N-1列不断递增
每次填格子都是L++,R++，这样保证斜着走！

//然后从副对角开始推理for (int j = 1; j < N; j++) {int L = 0;//行int R = j;//这样代表挨个操作副对角线--一会L++,R++//这种操作对角线的模式，学一下while (L < N && R < N) {

整体填表就是这样的代码：

//既然是俩递归函数，显然就是要填写两个表f,和s//而且，两个表的递归是相互推理的，那就是表之间相互推理，//怎么推，还得画个图，看笔记//根据终止条件，我们能得到第一批值，那就是对角线，一个是arr[L],一个是全0//表是一个矩阵，L*R的矩阵，L从0--N，R，从0--N//最后要求的其实是max（f[0][N-1],s[0][N-1])//然后f表往往还得看s表，由递归函数可知，假设我点在L,R处// 往往f表由s的L+1，或者R-1来推理，也就是我一个点的下边一个点，// 或者我一点的左边一个点，也就是我们填表，只需要考虑对角线右边那些//直到我们填写结束，拿到f[0][N-1],和s[0][N-1],求取最大值public static int getMaxValue2(int[] arr){if (arr == null || arr.length == 0) return 0;int N = arr.length;int[][] f = new int[N][N];//造表--默认全0int[][] s = new int[N][N];//造表--默认全0//根据终止条件，填写对角线for (int i = 0; i < N; i++) {f[i][i] = arr[i];//s表，全0}//然后从副对角开始推理for (int j = 1; j < N; j++) {int L = 0;//行int R = j;//这样代表挨个操作副对角线--一会L++,R++//这种操作对角线的模式，学一下while (L < N && R < N) {//对于所有副对角线元素//根据暴力递归来--先手先拿//拿左边int p1 = arr[L] + s[L + 1][R];//拿右边int p2 = arr[R] + s[L][R - 1];f[L][R] = Math.max(p1, p2);//我一定拿最好的//然后后手拿//如果先手拿走了Lint p3 = f[L + 1][R];//如果先手拿走了Rint p4 = f[L][R - 1];//咋招我都只能拿最次的s[L][R] = Math.min(p3, p4);L++;R++;//都递增就是去副对角线一侧，斜着走}}return Math.max(f[0][N - 1], s[0][N - 1]);//最终返回的最值}

测试一下：

    public static void test2(){int[] arr = {3, 100, 7, 10};int[] arr2 = {3, 100, 7};System.out.println("\n数组1：");for(Integer i : arr) System.out.print(i +" ");System.out.println();System.out.println(getMaxValue3DP(arr));System.out.println(getMaxValue2(arr));System.out.println("\n数组2：");for(Integer i : arr2) System.out.print(i +" ");System.out.println();System.out.println(getMaxValue3DP(arr2));System.out.println(getMaxValue2(arr2));}public static void main(String[] args) {
//        test();test2();}

结果：

数组1：
3 100 7 10 
110
110数组2：
3 100 7 
100
100

看见没？
斜着填表也行，只不过没有横着填来得方便和直接，但是也是最优解！！！
好好了解一下哦

总结

提示：重要经验：

1）暴力递归DP2：从L–R范围上的尝试模型，考虑L或R位置的情况，然后返回各自情况下的最好答案
2）从暴力递归修改为动态规划的代码，就是填表，这里是范围上的填表方式，有固定的的套路，先主对角，副对角，然后倒回来填，有时候，两个表相互依赖，怎么依赖，完全看暴力递归的代码来改写！
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。