两种折线的等距离分割方法（折线等分点）的python源码实现与比较 比例单元法与分步法

之前写过比例单元分割，现在修改如下getSplitXY，返回不含原来折点折线等分点数组与含原来折点的两个数组。经过比较检验，比例单元法与分步法的时间效率与N,n有关，见注释，分步法只返回包含原来折点的等分数组，可自行优化。代码如下：

import math
import time
import randomimport matplotlib.pyplot as plt# 与N n定有关，但还有其他因素，有时候第一种快，有时候第二种快 表面看有第一种性能更好；但因为前者有些不够完善，有影响，因此两种方法均可行
N = random.randint(5, 60)  # 第二种考虑因素多，某些情况会更加直观得出结果，因此有时候快，但是数据量越大，不确定因素越大，因此时间差距拉开
# 时间计算  N-n差值越大，用分步法，N-n越小，用比例法，正常情况差不多
line_coords = [[0, 0]]
print(f'N原始分段数值取：{N}')
while N >= 0:dx = random.randint(-1, 5)dy = random.randint(-1, 5)x = line_coords[len(line_coords) - 1][0] + dxy = line_coords[len(line_coords) - 1][1] + dyline_coords.insert(len(line_coords), [x, y])N = N - 1
n = random.randint(5,20)# 100段分1000以上会快一点
print(f'n目标等量分割值取：{n}')
# 总注释：比例单元分割法   不带详细注释版
print(f'原始坐标：{line_coords}')
t0 = time.time()# 分步法
def split_line(line_coords, n):# 计算折线总长度total_len = 0for i in range(len(line_coords) - 1):total_len += ((line_coords[i][0] - line_coords[i + 1][0]) ** 2 + (line_coords[i][1] - line_coords[i + 1][1]) ** 2) ** 0.5# 计算等分长度dis = total_len / n# 初始化等分点数组split_points = [line_coords[0]]# 计算等分点坐标i = 0while i < len(line_coords) - 1:# 计算当前线段长度cur_len = ((line_coords[i][0] - line_coords[i + 1][0]) ** 2 + (line_coords[i][1] - line_coords[i + 1][1]) ** 2) ** 0.5if cur_len < dis:# 如果当前线段长度小于等分长度，则跳过该线段dis -= cur_leni += 1else:# 计算等分点坐标ratio = dis / cur_lenx = line_coords[i][0] + ratio * (line_coords[i + 1][0] - line_coords[i][0])y = line_coords[i][1] + ratio * (line_coords[i + 1][1] - line_coords[i][1])split_points.append([x, y])line_coords.insert(i + 1, [x, y])dis = total_len / ni += 1# 确保最后一个点是折线的最后一个点if split_points[-1] != line_coords[-1]:split_points.append(line_coords[-1])return split_points# 比例归元法
def getSplitXY(array_xy,n):# 直角坐标距离计算 可以模拟经纬度距离 经过检验，不影响经纬度结果，这里使用直角坐标系距离计算# 提示：网络文章计算根据经纬度计算距离的函数方法可能有误，请自行检测def getDisArrDxy(array_xy):disArr = []dxy = []i = 0while i < len(array_xy) - 1:dx = array_xy[i + 1][0] - array_xy[i][0]dy = array_xy[i + 1][1] - array_xy[i][1]dis = (dx * dx + dy * dy) ** 0.5dxy.insert(i, [dx, dy])disArr.insert(i, dis)i = i + 1if i == len(array_xy) - 1:breakreturn disArr, dxyDisDxy = getDisArrDxy(array_xy)newdisArr = DisDxy[0]newDxy = DisDxy[1]# print(newDxy)# 等距离分隔值 分割常量dis = sum(newdisArr) / ndef IsEqual(x, y):IsEqual = FalseN1 = abs(x - y)if N1 < 0.000000001:IsEqual = Truereturn IsEqualdef IsInt(x):IsInt = FalseN1 = math.ceil(x) - xN2 = x - math.floor(x)if N1 < 0.000000001:x = math.ceil(x)return xif N2 < 0.000000001:x = math.floor(x)return xelse:return IsInt# 获取与分隔值比例数组 ArrDis 各分段Dis[i]/Dis# 比例初步整化 核心1def getIntRes(arrArr, array_xy):insert_xy = array_xy.copy()scale = arrArr.copy()# 剩余dis remanent 每一段最后一个取点位置 参考起点首个def getremanSc(scale):res = []sum = 0float = 0nn = 1  # 第1段开始取 目标段for i in range(0, len(scale)):sum = sum + scale[i]sc = sum / disif sc <= nn:  # 可插点的索引float = 1else:nn = math.ceil(sc)float = (scale[i] - (sum % dis)) / scale[i]res.insert(len(res), float)return resremanSc = getremanSc(scale)# 每一段第一个取点位置 参考起点首个def getFirst(scale):res = []sum = 0float = 0nn = 1  # 第1段开始取 目标段for i in range(0, len(scale)):sum = sum + scale[i]sc = sum / disif sc < nn:  # 可插点的索引float = 1else:nn = math.ceil(sc)float = 1 - (scale[i] - (sum % dis)) / scale[i]res.insert(len(res), float)return res#  每一段第一个取点位置  、参考起点尾scale.reverse()intSC = getFirst(scale)intSC.reverse()equalPts=[]# 整数化 比例分割def getIntSc(insert_xy, newDxy, intSC, remanSc):res = insert_xy.copy()j = 0for i in range(0, len(insert_xy) - 1):x0 = insert_xy[i][0] + newDxy[i][0] * intSC[i]y0 = insert_xy[i][1] + newDxy[i][1] * intSC[i]x1 = insert_xy[i][0] + newDxy[i][0] * remanSc[i]y1 = insert_xy[i][1] + newDxy[i][1] * remanSc[i]if IsEqual(insert_xy[i][0], x0) == True and IsEqual(insert_xy[i][1], y0) == True:res.insert(i + j + 1, [x1, y1])j = j + 1elif IsEqual(insert_xy[i+1][0], x1) == True and IsEqual(insert_xy[i+1][1], y1)==True:continueelse:if IsEqual(x0, x1) == True and IsEqual(y0, y1) == True:res.insert(i + j + 1, [x1, y1])j = j + 1else:res.insert(i + j + 1, [x0, y0])j = j + 1res.insert(i + j + 1, [x1, y1])j = j + 1return res# ("整数化 比例分割")res = getIntSc(insert_xy, newDxy, intSC, remanSc)return resgetIntxy = getIntRes(newdisArr, array_xy)resxy = getDisArrDxy(getIntxy)# cell单元化def getresxy(Intxy, intDisXY):rexy = Intxy.copy()j = 0for i in range(0, len(Intxy) - 1):if intDisXY[0][i] > dis:nn = (intDisXY[0][i] / dis)nn = IsInt(nn)ii = 1while ii < nn:x = Intxy[i][0] + ((((ii) * dis)) / intDisXY[0][i]) * intDisXY[1][i][0]y = Intxy[i][1] + ((((ii) * dis)) / intDisXY[0][i]) * intDisXY[1][i][1]if IsEqual(x,Intxy[i+1][0])==True and IsEqual(y,Intxy[i+1][1])==True:breakelse:rexy.insert(i + j + 1, [x, y])j = j + 1ii = ii + 1return rexyres_xy = getresxy(getIntxy, resxy)#print(res_xy)# cell 不含原折点坐标eqXY = [i for i in res_xy if i not in array_xy]#print(eqXY)return eqXY,res_xycellres = getSplitXY(line_coords, n)[0]
print(f'getSlitXY花费时间:{time.time() - t0:.11f}s')
print(cellres)
t1 = time.time()
xy = split_line(line_coords, n)
print(f'split_line花费时间:{time.time() - t1:.11f}s')
print(xy)
# 画出坐标系和折线
fig, ax = plt.subplots()
x_coords = [coord[0] for coord in line_coords]
y_coords = [coord[1] for coord in line_coords]
ax.plot(x_coords, y_coords)
# 计算折线长度# 画出等分点
x_coords = [coord[0] for coord in cellres]
y_coords = [coord[1] for coord in cellres]
ax.plot(x_coords, y_coords, 'ro')
# x_coord = [coord[0] for coord in xy]
# y_coord = [coord[1] for coord in xy]
# ax.plot(x_coord, y_coord, 'ro')plt.show()

getSplitXY的【0】示意图：

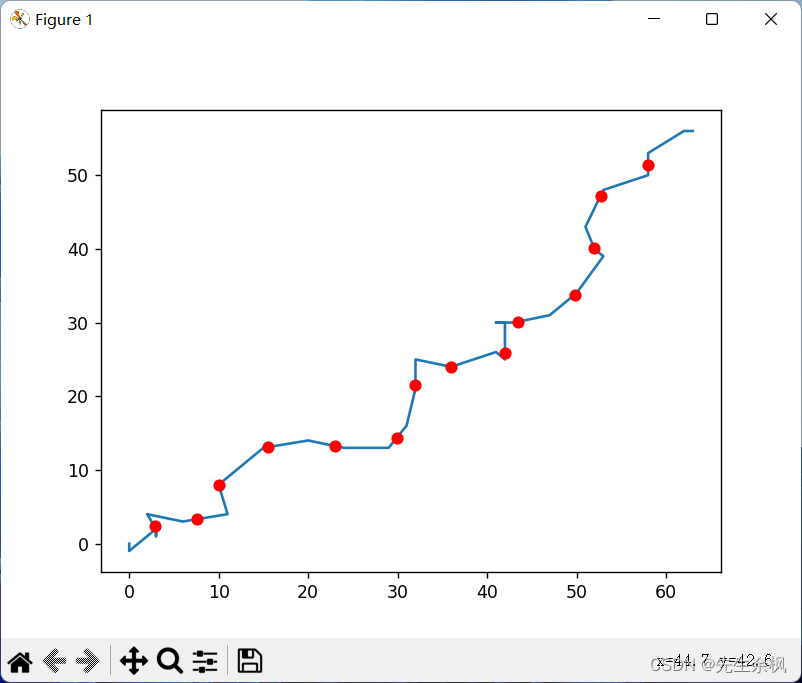
split_line函数目前只有一个小问题，就是每一段最后一个点实际与折线端点可能一样，但是不影响结果，可以用。

getSplitXY函数已经得到优化，相比于之前，大幅减少转化，原理参考上一篇文章。

split_line，getSlitXY的处理能力各有长处。一般情况都可以使用，大量数据的时候参考N,n差值