左神算法基础class3—题目9在行列都排好序的矩阵中找数

本文主要是介绍左神算法基础class3—题目9在行列都排好序的矩阵中找数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

左神算法基础class3—题目9在行列都排好序的矩阵中找数

1.题目
2.分析
3.核心代码
4.完整代码
5.输出结果

1.题目

【题目】给定一个有M*N的整型矩阵matrix和一个整数num，matrix的每一行和每一列都是排好序的。实现一个函数，判断K是否在matrix中。例如：{{1,3,5,6},{2,5,7,9},{4,6,8,10}} 如果num为7，返回true；如果K为11，返回false。
【要求】时间复杂度为O(N+M)，额外空间复杂度为O(1)。

2.分析

一般情况下对于从一组数中查找一个数不能达到复杂度只有O(N+M)，那么需要从题设的数据状况和问法出发找到解决思路。
本题可从数据状况出发，已知每一行每一列都是排好的，那么可以省去部分不必要的遍历。如下图所示，假设从右上角开始遍历，6>4，由于6所在的行和列都是排好序的，所以6下侧的9,10不可能找到4，因为他们比6大，自然大于4。这样就省去了不必要的过程。
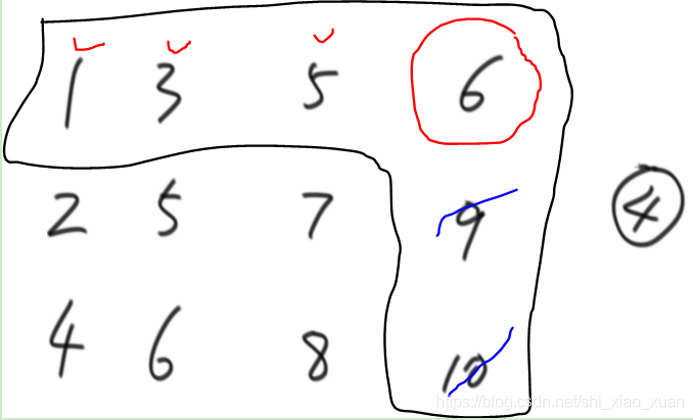
在这里插入图片描述

那么本题的思路如下：
（1）从右上角开始查找，如果当前数大于num，当前数左移继续查找；如果当前数小于num，当前数下移继续查找。如果当前数等于return true；
（2）由于查找只会向下方和左方前进，那么遍历的条件是当前数的范围在整个矩阵内，从右上角开始的话，条件是cur_col >= 0 && cur_row <= M -1

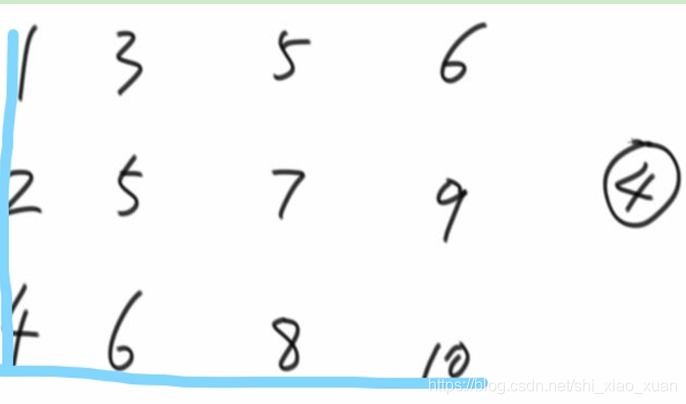
在这里插入图片描述

3.核心代码

在arr中查找num，cur_col 是纵向，cur_row是横向的坐标。

bool findnum(int arr[][N],int num)
{int cur_col = N - 1;int cur_row = 0;while(cur_col >= 0 && cur_row <= M -1){if(arr[cur_row][cur_col] < num){cur_row++;}else if(arr[cur_row][cur_col] > num){cur_col--;}elsereturn true;}return false;}

4.完整代码

#include<iostream>
#define M 3
#define N 4
using namespace std;bool findnum(int arr[][N],int num)
{int cur_col = N - 1;int cur_row = 0;while(cur_col >= 0 && cur_row <= M -1){if(arr[cur_row][cur_col] < num){cur_row++;}else if(arr[cur_row][cur_col] > num){cur_col--;}elsereturn true;}return false;}int main()
{int arr[M][N] = {{1,3,5,6},{2,5,7,9},{4,6,8,10}};cout<<findnum(arr,4)<<endl;system("pause");return 0;
}