PAT甲级1043 Is It a Binary Search Tree ：[C++题解]判断二叉搜索树BST、给定前序序列和中序序列

本文主要是介绍PAT甲级1043 Is It a Binary Search Tree ：[C++题解]判断二叉搜索树BST、给定前序序列和中序序列，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目分析

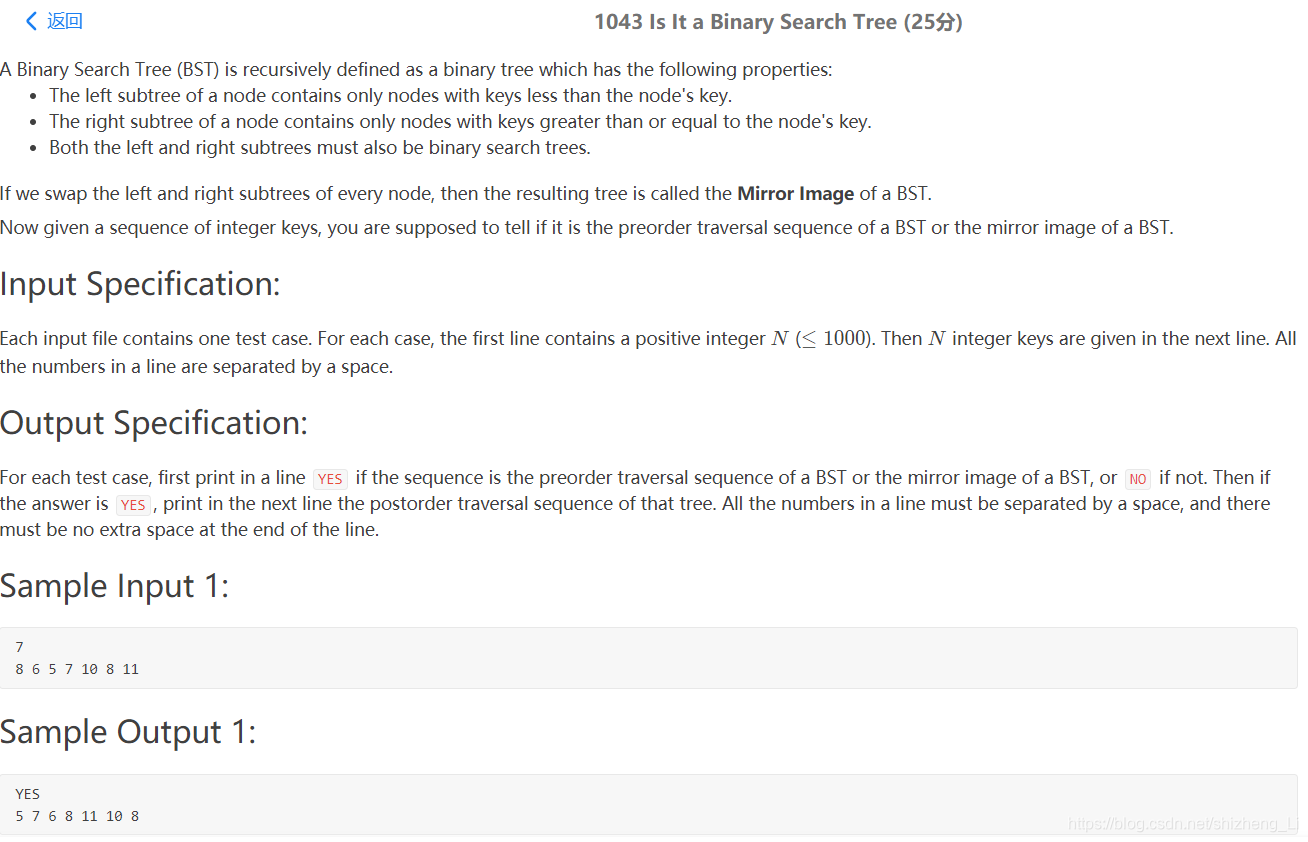
二叉搜索树（BST）：左子树小于根结点，右子树大于等于根结点。

二叉搜索树的中序遍历一定是有序序列。所谓中序遍历：先访问左子树，再访问根结点，最后访问右子树。

所以只要给定一棵BST，那么它的中序遍历序列就是一定的，从小到大有序。

现在本题给出一个序列，让判断是否是BST的前序序列，如果是，求出后序遍历。这相当于给了BST的前序遍历和中序遍历，让求后序遍历。

这道题就是前面做过的树的遍历那道题，PAT甲级1020 Tree Traversals：[C++题解]树的遍历、由中序序列和后序序列递归建树

思路是一样的， 先在前序遍历中找到根结点，然后把中序序列分成左子树和右子树。然后递归地找左子树的根结点和右子树的根结点。

这题稍微复杂一点，还需要判断一下是不是满足镜像BST，其实代码差不多。这里同时写进了函数bool build(int il ,int ir , int pl ,int pr,int type)中，依靠type来判断是原BST 还是镜像 BST

ac代码

#include<bits/stdc++.h>
using namespace std;const int N =1010;
int preorder[N] , inorder[N],postorder[N];
int cnt;bool build(int il ,int ir , int pl ,int pr,int type){//这个边界怎么确定的？ 为什么不是  il>= irif( il > ir) return true;int root = preorder[pl];int k ;if(type == 0){ //原树for(k =il;k<=ir; k++)if(inorder[k]==root)  break;if(k>ir) return false;}else{ //镜像树for(k=ir;k>=il;k--)if(root == inorder[k]) break;if(k<il) return false;}bool res =true;//若建左子树失败if( !build(il,k-1,pl+1, pl+1+(k-1-il),type) )  res =false;//若建右子树失败if( !build(k+1,ir,pr-(ir-k-1) ,pr,type) )      res =false;//由于是输出后序遍历，所以 postorder放在 两个递归后面；//如果是输出中序遍历，则需要把postorder放在两个递归中间。postorder[cnt++] = root;return res;}int main(){int n;cin>> n;for(int i=0;i <n ;i++){cin>>preorder[i];   inorder[i] =preorder[i];}//排序，就是中序遍历sort(inorder,inorder+n);//type == 0 表示原BST树if(build(0,n-1, 0,n-1, 0)){cout<<"YES"<<endl;cout<<postorder[0];for(int i=1;i<n;i++) cout<<" "<<postorder[i];cout<<endl;}else{  //否则type==1，表示镜像BST树reverse(inorder,inorder+n); //中序遍历就是逆置一下cnt=0; //这句cnt 清零必须加，因为这是从上一个if过来的，上面的cnt已经变了if(build(0,n-1,0,n-1,1)){ //镜像树是BSTcout<<"YES"<<endl;cout<<postorder[0];for(int i=1;i<n;i++) cout<<" "<<postorder[i];cout<<endl;} //不是BST，也不是镜像BST，则输出NOelse cout<<"NO"<<endl;}
}

题目链接

PAT甲级1043 Is It a Binary Search Tree

这篇关于PAT甲级1043 Is It a Binary Search Tree ：[C++题解]判断二叉搜索树BST、给定前序序列和中序序列的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---