本文主要是介绍【VRP问题】基于企鹅优化算法求解冷链配送物流车辆调度优化研究(Matlab代码实现),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1 概述
2 帝国企优化算法
3 运行结果
4 参考文献
5 Matlab代码实现
🎁专栏目录链接:
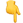
| 🌈🌈🌈 | 🌟🌟🌟 |
| 电气代码 | 智能算法及其应用 |
| 路径规划 | 神经网络预测 |
| 优化调度 | 图像处理 |
| 车间调度 | 信号处理 |
| 浪漫的她 | 我的哲思 |
| 数学建模 |
1 概述
在互联网的带动下,农产品冷链物流需求越来越大,而成本一直是制约冷链牧流发展的关键因素,如何有效降低冷链物流成本成为国家、企业和消费者共同关注的热点话题。与此同时,冷链物流市场的扩大以及消费者对服务品质的要求提升促使企业不得不提升自身服务质量,提高满意度来增加顾客黏性,在竞争激烈的场中占据一席之地。因此,本文的研究旨在通过合理的车辆调度和路径优化,在保证满意度处于高水平的情况下,使综合成本最低,为冷链物流企业的日常调度工作作提供依据。本文突破了仅考虑运输成本及单配送中心来优化冷链物流路径的局限性克服了传统遗传算法在求解VRP(Vehicle Routing Problem)问题的不足,提出了基于帝国企鹅优化算法求解冷链配送物流车辆调度优化研究,因而具有重要的理论和现实意义。
2 帝国企优化算法
自2018年Gaurav等[4提出帝企鹅优化算法以来,学者对初始帝企鹅优化算法进行研究并且寻求其进一步改进,希望可以将其用于不同类型的优化问题求解中。Jia等[6⒁I在帝企鹅优化算法的基础上,利用Masi嫡作为目标函数,提出一种改进帝企鹅优化算法,实验结果证明所提出的算法更适合于高维复杂卫星图像的分割。Kumar等使用基于量子的多目标帝企鹅优化算法进行自动聚类,以及应用于图像分割中。Santos等提出了多目标版本的帝企鹅优化算法,并且将提出的算法用于最佳特征选择与癌症分类。Baliarsingh 等[I将社会工程优化的莫因算法嵌入帝企鹅优化算法,增强了EPO算法的开发能力,成功的将医疗数据进行分类。Gaurav等[7]提出一个新的二元帝企鹅优化算法(BEPO)进行自动特征选择。Tang等对原始帝企鹅优化算法改进,提出一种改进EPO算法,用以优化住址建筑。Gaurav等!?"结合了多目标斑点鬣狗算法、樽海鞘群算法和帝企鹅优化算法的特征,提出新的混合多目标元启发式算法求解工程设计问题。Shrivastava将帝企鹅优化算法应用于限制使用无线电传感器网络污染的城市交通管理。
3 运行结果
这里仅展现部分图。
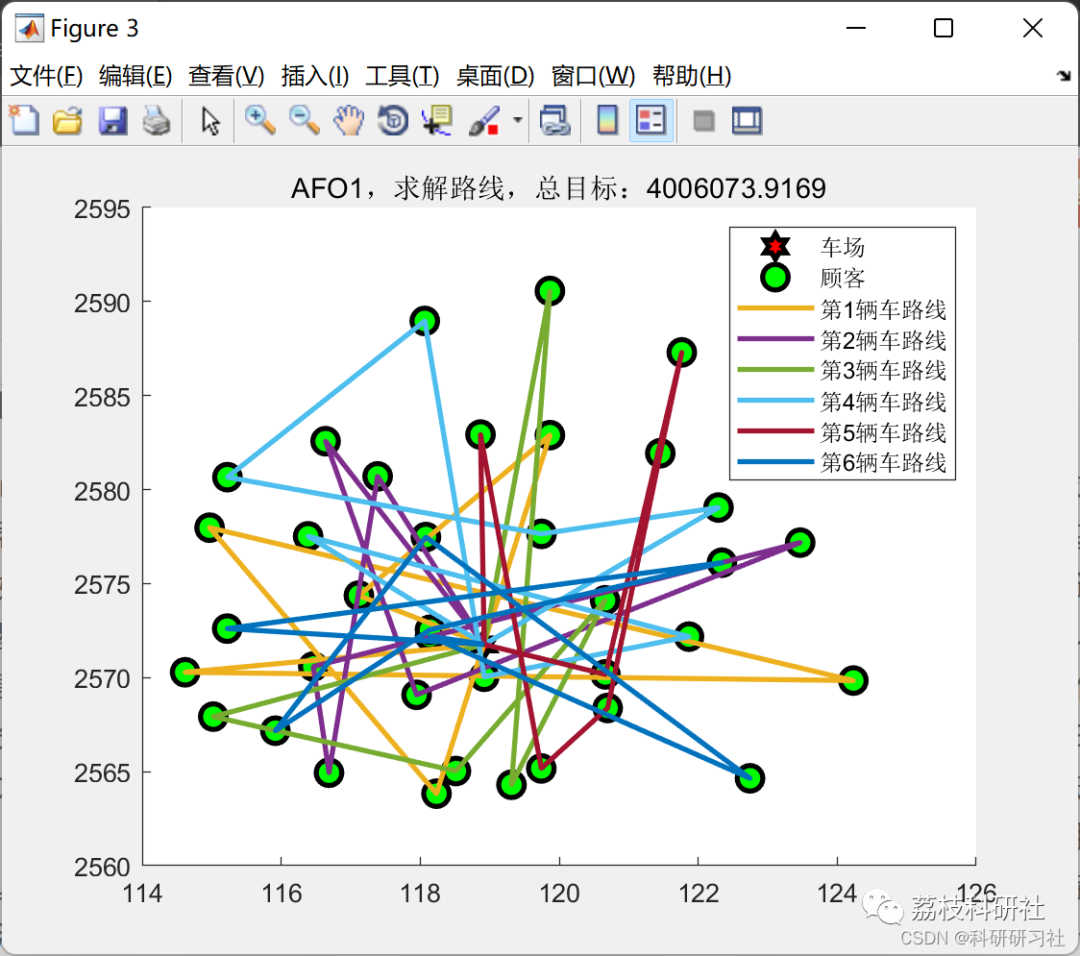
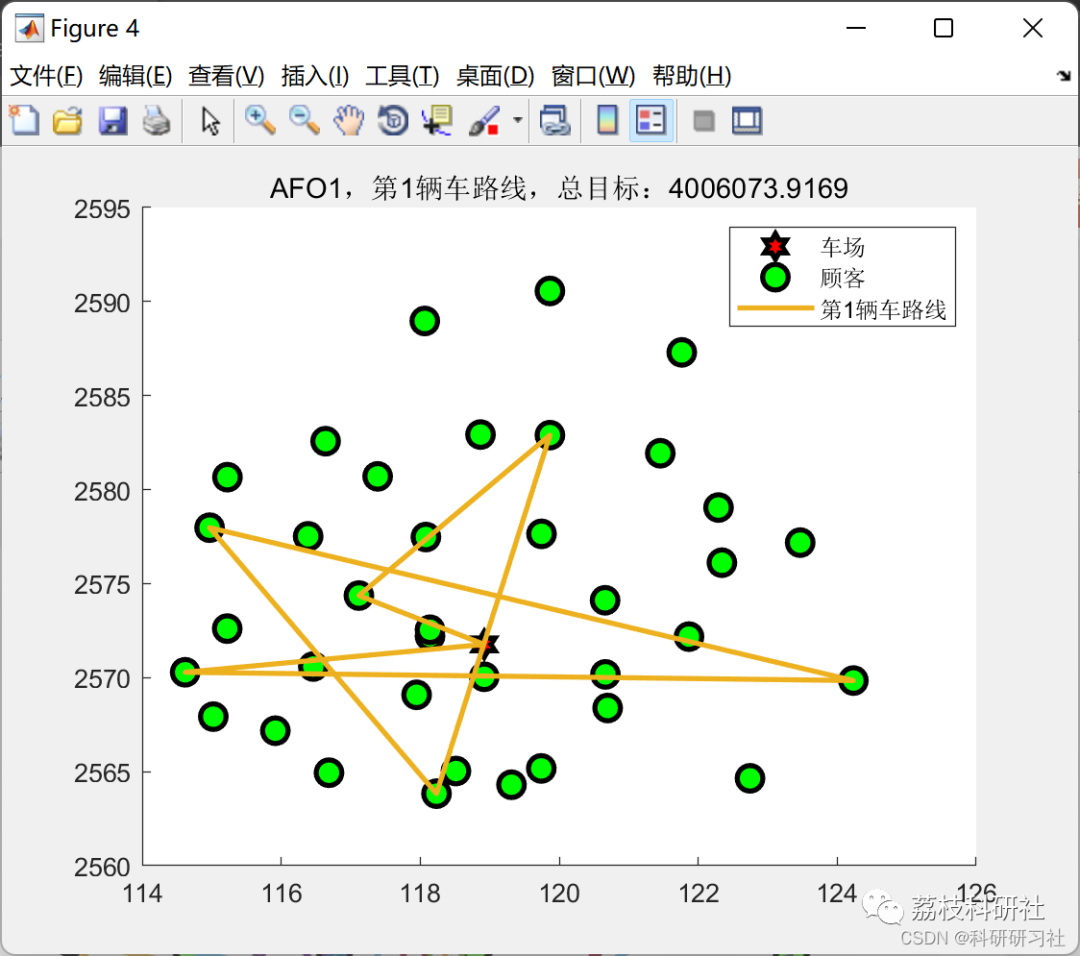

部分代码:
function drawPc(result1,option,data,str)figurehold onlegendStr=[{'车场'},{'顾客'}];plot(data.node(data.noCenter,2),data.node(data.noCenter,3),'h','LineWidth',2,...'MarkerEdgeColor','k',...'MarkerFaceColor','r',...'MarkerSize',10);plot(data.node(data.noNode,2),data.node(data.noNode,3),'o','LineWidth',2,...'MarkerEdgeColor','k',...'MarkerFaceColor','g',...'MarkerSize',10);for i=1:length(result1.recording.Path)path=[result1.recording.Path{i}(:,1);1];plot(data.node(path,2),data.node(path,3),'-','LineWidth',2);legendStr=[legendStr,{['第',num2str(i),'辆车路线']}];endlegend(legendStr);title([str,',求解路线,总目标:',num2str(result1.fit)]);for i=1:length(result1.recording.Path)figurehold onlegendStr=[{'车场'},{'顾客'}];plot(data.node(data.noCenter,2),data.node(data.noCenter,3),'h','LineWidth',2,...'MarkerEdgeColor','k',...'MarkerFaceColor','r',...'MarkerSize',10);plot(data.node(data.noNode,2),data.node(data.noNode,3),'o','LineWidth',2,...'MarkerEdgeColor','k',...'MarkerFaceColor','g',...'MarkerSize',10);path=[result1.recording.Path{i}(:,1);1];plot(data.node(path,2),data.node(path,3),'-','LineWidth',2);legendStr=[legendStr,{['第',num2str(i),'辆车路线']}];legend(legendStr);title([str,',第',num2str(i),'辆车路线,总目标:',num2str(result1.fit)]);endend
function drawPc(result1,option,data,str) figure hold on legendStr=[{'车场'},{'顾客'}]; plot(data.node(data.noCenter,2),data.node(data.noCenter,3),'h','LineWidth',2,... 'MarkerEdgeColor','k',... 'MarkerFaceColor','r',... 'MarkerSize',10); plot(data.node(data.noNode,2),data.node(data.noNode,3),'o','LineWidth',2,... 'MarkerEdgeColor','k',... 'MarkerFaceColor','g',... 'MarkerSize',10); for i=1:length(result1.recording.Path) path=[result1.recording.Path{i}(:,1);1]; plot(data.node(path,2),data.node(path,3),'-','LineWidth',2); legendStr=[legendStr,{['第',num2str(i),'辆车路线']}]; end legend(legendStr); title([str,',求解路线,总目标:',num2str(result1.fit)]); for i=1:length(result1.recording.Path) figure hold on legendStr=[{'车场'},{'顾客'}]; plot(data.node(data.noCenter,2),data.node(data.noCenter,3),'h','LineWidth',2,... 'MarkerEdgeColor','k',... 'MarkerFaceColor','r',... 'MarkerSize',10); plot(data.node(data.noNode,2),data.node(data.noNode,3),'o','LineWidth',2,... 'MarkerEdgeColor','k',... 'MarkerFaceColor','g',... 'MarkerSize',10); path=[result1.recording.Path{i}(:,1);1]; plot(data.node(path,2),data.node(path,3),'-','LineWidth',2); legendStr=[legendStr,{['第',num2str(i),'辆车路线']}]; legend(legendStr); title([str,',第',num2str(i),'辆车路线,总目标:',num2str(result1.fit)]); endend
4 参考文献
部分理论来源于网络文献,如有侵权联系删除。
[1]李娜. 单亲遗传算法的冷链物流车辆路径问题(VRP)优化研究[D].燕山大学,2016.
5 Matlab代码实现
这篇关于【VRP问题】基于企鹅优化算法求解冷链配送物流车辆调度优化研究(Matlab代码实现)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


