MPC模型预测控制理论与实践

本文主要是介绍MPC模型预测控制理论与实践，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、基本概念

最有控制的动机是在约束条件下达到最优的系统表现。

模型预测控制（MPC，Model Predictive Control）是通过模型来预测系统在某一未来时间段内的表现来进行优化控制，多用于数位控制，通常用离散型状态空间表达。主要有三个主要部分构成，1模型；2预测；3控制（做决策）。模型，模型可以是机理模型，也可以是一个基于数据的模型。（例如深度学习训练得到的模型）预测，建立一个模型目的主要是用来做预测。控制（做决策），控制就是需要做出动作了，控制就是采取行动执行动作。

MPC主要有三步：

在k时刻：

1、估计/测量读取当前系统状态；

2、基于来进行最优化，离散系统代价函数为

3、只取作为控制输入施加在系统上。

在下一时刻重复以上三步，在下一步进行预测时使用的就是下一步的状态值，即滚动优化控制。

二、理论原理

1、二次规划的一般形式：

二次规划问题目前的优化理论提供了较完整的求解方法，可以利用诸多工具进行求解。这里的MPC问题最后能够归结为求解一个二次规划问题，即最小化代价函数。

2、MPC代价函数

对于一个离散系统

在k时刻进行观测，预测从k到N时刻的状态为：

输入为：

离散系统的代价函数为：

我们需要求解的是系统的输入，这就需要我们把状态项给消除掉。可以通过传感器或者状态估计得到系统当前的状态值，利用系统初始条件，以及上述离散状态方程，可以得到所有状态量用输入和初始值表达的形式：

令，，则有

代价函数可以化简为：

即

进一步可以化简为

其中。

该代价函数可以利用二次规划进行优化。

三、代码实践

问题：

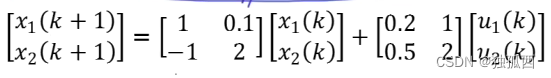
1、MPC_Test.m

%% 清屏clear ; close all; clc;%% 加载 optim package,若使用matlab，则注释掉此行pkg load optim;%%%%%%%%%%%%%%%%%%%%%%%%%%%% 第一步，定义状态空间矩阵%% 定义状态矩阵 A, n x n 矩阵A = [1 0.1; -1 2];n= size (A,1);%% 定义输入矩阵 B, n x p 矩阵B = [ 0.2 1; 0.5 2];p = size(B,2);%% 定义Q矩阵，n x n 矩阵Q=[100 0;0 1];%% 定义F矩阵，n x n 矩阵F=[100 0;0 1];%% 定义R矩阵，p x p 矩阵R=[1 0 ;0 .1];%% 定义step数量kk_steps=100; %% 定义矩阵 X_K， n x k 矩 阵X_K = zeros(n,k_steps);%% 初始状态变量值， n x 1 向量X_K(:,1) =[20;-20];%% 定义输入矩阵 U_K， p x k 矩阵U_K=zeros(p,k_steps);%% 定义预测区间KN=5;%% Call MPC_Matrices 函数 求得 E,H矩阵 [E,H]=MPC_Matrices(A,B,Q,R,F,N);%% 计算每一步的状态变量的值for k = 1 : k_steps %% 求得U_K(:,k)U_K(:,k) = Prediction(X_K(:,k),E,H,N,p);%% 计算第k+1步时状态变量的值X_K(:,k+1)=(A*X_K(:,k)+B*U_K(:,k));end%% 绘制状态变量和输入的变化subplot  (2, 1, 1);hold;for i =1 :size (X_K,1)plot (X_K(i,:));endlegend("x1","x2")hold off;subplot (2, 1, 2);hold;for i =1 : size (U_K,1)plot (U_K(i,:));endlegend("u1","u2")

2、MPC_Matrices.m

function  [E , H]=MPC_Matrices(A,B,Q,R,F,N)n=size(A,1);   % A 是 n x n 矩阵, 得到 np=size(B,2);   % B 是 n x p 矩阵, 得到 p%%%%%%%%%%%%M=[eye(n);zeros(N*n,n)]; % 初始化 M 矩阵. M 矩阵是 (N+1)n x n的， % 它上面是 n x n 个 "I", 这一步先把下半部% 分写成 0 C=zeros((N+1)*n,N*p); % 初始化 C 矩阵, 这一步令它有 (N+1)n x NP 个 0% 定义M 和 C tmp=eye(n);  %定义一个n x n 的 I 矩阵%　更新Ｍ和Cfor i=1:N % 循环，i 从 1到 Nrows =i*n+(1:n); %定义当前行数，从i x n开始，共n行 C(rows,:)=[tmp*B,C(rows-n, 1:end-p)]; %将c矩阵填满tmp= A*tmp; %每一次将tmp左乘一次AM(rows,:)=tmp; %将M矩阵写满end % 定义Q_bar和R_barQ_bar = kron(eye(N),Q);Q_bar = blkdiag(Q_bar,F);R_bar = kron(eye(N),R); % 计算G, E, HG=M'*Q_bar*M; % G: n x nE=C'*Q_bar*M; % E: NP x nH=C'*Q_bar*C+R_bar; % NP x NP end

3、Prediction.m

function u_k= Prediction(x_k,E,H,N,p)U_k = zeros(N*p,1); % NP x 1U_k = quadprog(H,E*x_k);u_k = U_k(1:p,1); % 取第一个结果end

四、应用总结

模型预测控制(Model Predictive Control, MPC)是一种先进的闭环控制算法，它通过建立系统的数学模型，预测未来一定时间内的系统状态，并基于优化算法计算出最优控制信号。MPC具有以下优缺点：

优点：

1. 高精度控制：除了考虑当前系统状态外，还能预测未来一段时间的系统状态，因此可以更精确地控制系统；

2. 鲁棒性强：MPC可以通过修改控制器优化问题的约束来应对外部干扰和不确定性，提高控制系统的鲁棒性；

3. 可处理复杂系统：MPC可以建立各种复杂系统的数学模型，并通过计算机算法进行优化，适用于多变量、非线性系统等；

4. 可满足控制要求：MPC可以将多个控制要求统一优化，因此可以满足多个控制目标同时达到。

缺点：

1. 计算复杂：MPC优化问题通常是一个非凸、非线性的问题，要求大量的计算资源和高效的算法，导致计算复杂度很高；

2. 运行速度慢：由于计算复杂度高，MPC的运行速度相比其他控制算法要慢很多，因此只能应用于响应速度要求不高的稳态控制系统；

3. 受模型误差影响：MPC算法是基于系统模型来进行优化的，因此系统模型误差会直接影响算法控制效果。因此，建立准确的系统模型是MPC算法应用的关键。

MPC主要还是应用在控制领域，在自动驾驶、无人机飞行控制、平衡车的控制、四足控制中有着广泛的应用。MPC这种将优化与控制结合的思想也许可以用在更多领域。

参考资料：

【【MPC模型预测控制器】1_最优化控制和基本概念】 https://www.bilibili.com/video/BV1cL411n7KV/?share_source=copy_web&vd_source=24db73a73cddacddda48febd1ffc28ef

网络资料等。

这篇关于MPC模型预测控制理论与实践的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---