机器学习：VAE(Variational Autoencoder) 模型

本文主要是介绍机器学习：VAE(Variational Autoencoder) 模型，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

VAE 模型是一种有趣的生成模型，与GAN相比，VAE 有更加完备的数学理论（引入了隐变量），理论推导更加显性，训练相对来说更加容易。

VAE 可以从神经网络的角度或者概率图模型的角度来解释。

VAE 全名叫 变分自编码器，是从之前的 auto-encoder 演变过来的，auto-encoder 也就是自编码器，自编码器，顾名思义，就是可以自己对自己进行编码，重构。所以 AE 模型一般都由两部分的网络构成，一部分称为 encoder, 从一个高维的输入映射到一个低维的隐变量上，另外一部分称为 decoder, 从低维的隐变量再映射回高维的输入：

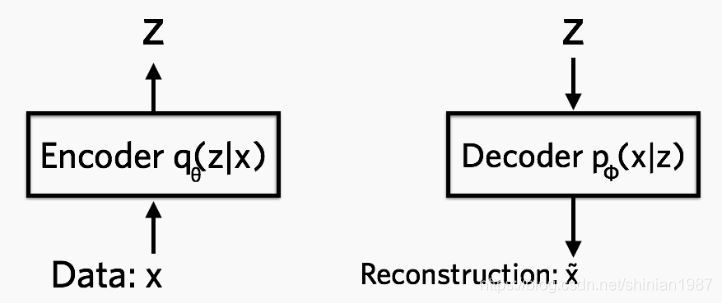
VAE模型

如上图所示，encoder 网络中的参数为 $\theta$, decoder 中网络中的参数为 $\varphi$，$\theta$ 就是让网络从 $x$ 到 $z$ 的映射，而 $\varphi$ 可以让网络完成从 $z$ 到 $x$ 的重构，encoder 可以表示成 $q_{\theta }(z|x)$，decoder 可以表示成 $p_{\varphi }(x|z)$，基于这个，可以构造如下的损失函数：

$$l_i(\theta ,\varphi )=-E_{z\sim q_{\theta }(z|x_i)}[log(p_{\varphi }(x_i|z))]+KL(q_{\theta }(z|x_i)||p(z))$$

上面的第一部分，可以看做是重建 loss，就是从 $x\sim z\sim x$ 的这样一个过程，可以表示成上面的熵的形式，也可以表示成最小二乘的形式，这个取决于$x$本身的分布。后面的 KL 可以看做是正则项，$q_{\theta }(z|x)$ 可以看成是根据$x$推导出来的$z$的一个后验分布，$p(z)$可以看成是$z$的一个先验分布，我们希望这两个的分布尽可能的拟合，所以这一点是VAE与GAN的最大不同之处，VAE对隐变量$z$是有一个假设的，而GAN里面并没有这种假设。 一般来说，$p(z)$都假设是均值为0，方差为1的高斯分布 $\mathcal{N}(0,1)$。

如果没有 KL 项，那VAE就退化成一个普通的AE模型，无法做生成，VAE中的隐变量是一个分布，或者说近似高斯的分布，通过对这个概率分布采样，然后再通过decoder网络，VAE可以生成不同的数据，这样VAE模型也可以被称为生成模型。

下面看看每个部分的代码实现：

如果只是基于 MLP 的VAE，就是普通的全连接网络：

import tensorflow as tf
from tensorflow.contrib import layers## encoder 模块
def fc_encoder(x, latent_dim, activation=None):e = layers.fully_connected(x, 500, scope='fc-01')e = layers.fully_connected(e, 200, scope='fc-02')output = layers.fully_connected(e, 2 * latent_dim, activation_fn=activation,scope='fc-final')return output## decoder 模块
def fc_decoder(z, observation_dim, activation=tf.sigmoid):x = layers.fully_connected(z, 200, scope='fc-01')x = layers.fully_connected(x, 500, scope='fc-02')output = layers.fully_connected(x, observation_dim, activation_fn=activation,scope='fc-final')return output

关于这几个 loss 的计算：

   ## KL lossdef _kl_diagnormal_stdnormal(mu, log_var):var = tf.exp(log_var)kl = 0.5 * tf.reduce_sum(tf.square(mu) + var - 1. - log_var)return kl## 基于高斯分布的重建lossdef gaussian_log_likelihood(targets, mean, std):se = 0.5 * tf.reduce_sum(tf.square(targets - mean)) / (2*tf.square(std)) + tf.log(std)return se## 基于伯努利分布的重建lossdef bernoulli_log_likelihood(targets, outputs, eps=1e-8):log_like = -tf.reduce_sum(targets * tf.log(outputs + eps)+ (1. - targets) * tf.log((1. - outputs) + eps))return log_like

可以看到，重建loss，如果是高斯分布，就是最小二乘，如果是伯努利分布，就是交叉熵，关于高斯分布的 KL loss 的详细推导，可以看下面这个帖子：

https://zhuanlan.zhihu.com/p/22464760

过程很复杂，结果很简单。如果有两个高斯分布 ${\mathcal{N}}_1\sim ({\mu }_1,{\sigma }_1^2)$，${\mathcal{N}}_2\sim ({\mu }_2,{\sigma }_2^2)$，最后这两个分布的 KL 散度是：

$$KL(N_1||N_2)=log(\frac{{\sigma }_2}{{\sigma }_1})+\frac{{\sigma }_1^2+({\mu }_1-{\mu }_2{)}^2}{2{\sigma }_2^2}-\frac{1}{2}$$

VAE 中，我们已经假设 $z$ 的先验分布是$\mathcal{N}(0,1)$，所以 ${\mu }_2=0,{\sigma }_2^2=1$，代入上面的公式，可以得到：

$$los{s}_{KL}=-log({\sigma }_1)+\frac{{\sigma }_1^2+{\mu }_1^2}{2}-\frac{1}{2}$$

参考：

https://jaan.io/what-is-variational-autoencoder-vae-tutorial/
https://github.com/wuga214/IMPLEMENTATION_Variational-Auto-Encoder

这篇关于机器学习：VAE(Variational Autoencoder) 模型的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---