本文主要是介绍【MVP矩阵】裁剪空间、NDC空间、屏幕空间,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
裁剪空间概述
裁剪空间是一个顶点乘以MVP矩阵之后所在的空间,Vertex Shader的输出就是在裁剪空间上(划重点)
NDC空间概述
接上面,由GPU自己做透视除法将顶点转到NDC空间
两者的转换
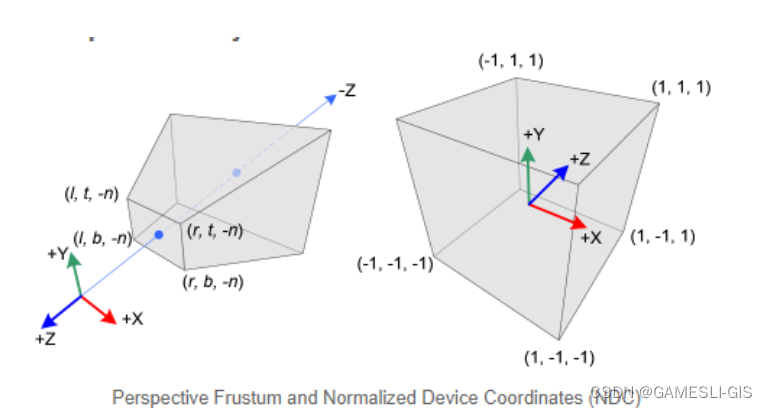
透视除法将Clip Space顶点的4个分量都除以w分量,就从Clip Space转换到了NDC了。
而NDC是一个长宽高取值范围为[-1,1]的立方体,超过这个范围的顶点,会被GPU剪裁。

屏幕空间
Vertex Shader的输出在Clip Space,那Fragment Shader的输入在什么空间?不是NDC,而是屏幕空间Screen Space。
我们前面说到Vertex Shader的输出在Clip Space,接着GPU会做透视除法变到NDC。这之后GPU还有一步,应用视口变换,转换到Window Space(Screen Space),输入给Fragment Shader:
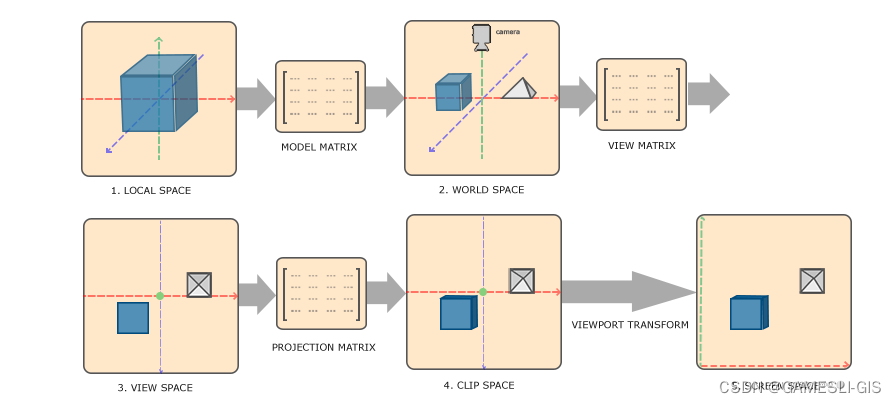
坐标系转换流程:
(Vertex Shader MVP) => Clip Space => (透视除法(GPU自己完成)) => NDC => (视口变换(GPU自己完成)) => Window Space => (Fragment Shader)
前面提到了Fragment Shader的输入是经过视口变换后的坐标,Shader中访问的方法是:OpenGL中通过gl_FragCoord来访问
此输入参数的xy分量表示Screen Space的坐标,z表示写入到深度缓冲中的值,那么w分量表示什么呢?OpenGL中gl_FragCoord来说,存的是1/w
备注
参考
https://sites.cs.ucsb.edu/~lingqi/teaching/games101.htm
这篇关于【MVP矩阵】裁剪空间、NDC空间、屏幕空间的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






