本文主要是介绍中国剩余定理Chinese remainder theorem(CRT),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
中国剩余定理
孙子定理, Chinese remainder theorem(CRT)
参考 : 百度百科-中国剩余定理
有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
x=2mod3
x=3mod5
x=2mod7
// 求解得: x = 23
模算术和数论有相关算法可以解决这个问题,参考资料:《密码学原理与实践第三版》5.2章节 更多数论知识
1. Euclidean欧几里得算法
Euclidean算法的基本形式,可以给出两个正整数a、b的最大公因子Greatest Common Divisor(GCD)。

举例计算 : g c d ( 99 , 63 ) gcd(99,63) gcd(99,63)
99 = 1 ⋅ 63 + 36 99 = 1 · 63 + 36 99=1⋅63+36
63 = 1 ⋅ 36 + 27 63 = 1 · 36 + 27 63=1⋅36+27
36 = 1 ⋅ 27 + 9 36 = 1 · 27 + 9 36=1⋅27+9
27 = 3 ⋅ 9 + 0 27 = 3 · 9 + 0 27=3⋅9+0
g c d ( 99 , 63 ) = ( 63 , 36 ) = ( 36 , 27 ) = ( 27 , 9 ) = 9 gcd(99, 63) = (63, 36) = (36, 27) = (27, 9) = 9 gcd(99,63)=(63,36)=(36,27)=(27,9)=9
2. 扩展欧几里得算法,求模乘逆: b − 1 ( m o d a ) b^{-1}\pmod a b−1(moda)
-
是否存在整数s,t,使得 s a + t b = ( a , b ) sa+tb=(a,b) sa+tb=(a,b)?
如果存在, 且 ( a , b ) = 1 (a,b)=1 (a,b)=1,则有 s a + t b = 1 sa+tb=1 sa+tb=1
两边模a之后,得到 t b ≡ 1 ( m o d a ) tb\equiv 1\pmod a tb≡1(moda),即
t = b − 1 ( m o d a ) t=b^{-1}\pmod a t=b−1(moda) -
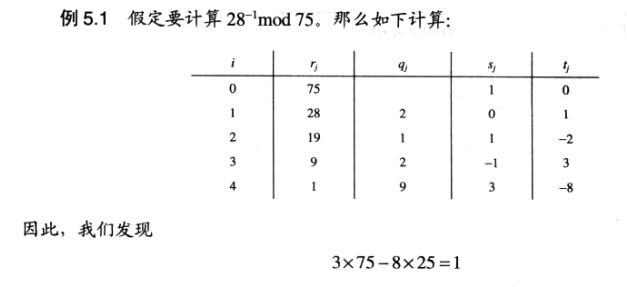
书上例5.1计算 2 8 − 1 ( m o d 75 ) 28^{-1}\pmod{75} 28−1(mod75),如何计算s、t?
定义 t j = { 0 , if j = 0 ; 1 , if j = 1 ; t j − 2 − q i − 1 t j − 1 , if j ≥ 2 ; t_j = \begin{cases} 0, &\text{if } j=0; \\ 1, &\text{if } j=1; \\ t_{j-2}-q_{i-1}t_{j-1}, &\text{if } j\ge 2; \end{cases} tj=⎩⎪⎨⎪⎧0,1,tj−2−qi−1tj−1,if j=0;if j=1;if j≥2;定义 s j = { 1 , if j = 0 ; 0 , if j = 1 ; s j − 2 − q i − 1 s j − 1 , if j ≥ 2 ; s_j = \begin{cases} 1, &\text{if } j=0; \\ 0, &\text{if } j=1; \\ s_{j-2}-q_{i-1}s_{j-1}, &\text{if } j\ge 2; \end{cases} sj=⎩⎪⎨⎪⎧1,0,sj−2−qi−1sj−1,if j=0;if j=1;if j≥2;
-
书上模乘逆算法

-
Js版本模乘逆算法
题目:利用求逆算法,计算 104729 8 − 1 ( m o d 15484863 ) = 6926637 1047298^{-1}\pmod{15484863} = 6926637 1047298−1(mod15484863)=6926637
function MultiplicativeInverse(a, b) {let a0 = alet b0 = blet t0 = 0let t = 1let q = Math.floor(a0 / b0)let r = a0 - q * b0let j = 0// console.log("j", "rj", "qj", "tj")// console.log(j, a0, "-", t0)let qtemp = qwhile (r > 0) {const temp = (t0 - q * t) % at0 = tt = tempa0 = b0b0 = rq = Math.floor(a0 / b0)r = a0 - q * b0j++console.log(j, a0, qtemp, t0)qtemp = q}if (b0 !== 1) {return false} else {console.log(j + 1, b0, a0, t)return t}
}- 测试结果
console.log(MultiplicativeInverse(75, 28))
j rj qj tj
0 75 - 0
1 28 2 1
2 19 1 -2
3 9 2 3
4 1 9 -8
-8
console.log(MultiplicativeInverse(15485863, 104729))
j rj qj tj
0 15485863 - 0
1 104729 147 1
2 90700 1 -147
3 14029 6 148
4 6526 2 -1035
5 977 6 2218
6 664 1 -14343
7 313 2 16561
8 38 8 -47465
9 9 4 396281
10 2 4 -1632589
11 1 2 6926637
6926637
3. 求解同余方程组
中国剩余定理,是求解以下的一元线性同余方程组的过程:
x ≡ a 1 ( m o d m 1 ) x\equiv a_1\pmod {m_1} x≡a1(modm1)
x ≡ a 2 ( m o d m 2 ) x\equiv a_2\pmod {m_2} x≡a2(modm2)
⋮ \vdots ⋮
x ≡ a 1 ( m o d m 1 ) x\equiv a_1\pmod {m_1} x≡a1(modm1)
中国剩余定理断言这个方程组有模 M = m 1 × m 2 × . . . × m r M=m_1\times m_2\times ...\times m_r M=m1×m2×...×mr的唯一解, 其解为:
x = ∑ i = 1 r a i M i y i ( m o d M ) x=\displaystyle\sum_{i=1}^ra_iM_iy_i \pmod M x=i=1∑raiMiyi(modM)
其中 M i = M / m i , y i = m i − 1 ( m o d m i ) , 1 ≤ i ≤ r M_i = M/m_i, y_i=m_i^{-1}\pmod{m_i}, 1\le i\le r Mi=M/mi,yi=mi−1(modmi),1≤i≤r

现在求解:有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
- M = 3 ∗ 5 ∗ 7 = 105 , M 1 = 5 ∗ 7 = 35 , M 2 = 3 ∗ 7 = 21 , M 3 = 3 ∗ 5 = 15 M=3*5*7=105,M_1=5*7=35,M_2=3*7=21,M_3=3*5=15 M=3∗5∗7=105,M1=5∗7=35,M2=3∗7=21,M3=3∗5=15
- y 1 = M 1 逆 模 m 1 = 35 逆 模 3 = 2 , y 2 = 21 逆 模 5 = 1 , y 3 = 15 逆 模 7 = 1 y_1=M_1逆模m_1=35逆模3=2,y_2=21逆模5=1,y_3=15逆模7=1 y1=M1逆模m1=35逆模3=2,y2=21逆模5=1,y3=15逆模7=1
- x = ( a 1 M 1 y 1 + a 2 M 2 y 2 + a 3 M 3 y 3 ) m o d M = ( 2 ∗ 35 ∗ 2 + 3 ∗ 21 ∗ 1 + 2 ∗ 15 ∗ 1 ) ( m o d 105 ) = 23 x=( a_1M_1y_1+a_2M_2y_2+a_3M_3y_3 )modM = (2*35*2+3*21*1+2*15*1) \pmod{105} = 23 x=(a1M1y1+a2M2y2+a3M3y3)modM=(2∗35∗2+3∗21∗1+2∗15∗1)(mod105)=23
JS算法:
// 输入:[[2,3],[3,5],[2,7]]
function CRT(array) {let x = 0,M = 1for (let i = 0; i < array.length; i++) {const element = array[i]; // [2,3]M = M * element[1]}for (let i = 0; i < array.length; i++) {const element = array[i]; // [2,3]let Mi = M / element[1]let yi = MultiplicativeInverse(element[1], Mi)if (yi < 0) {yi = element[1] + yi}console.log(element[0], Mi, yi)x = x + element[0] * Mi * yi}console.log(x + "mod" + M + "=" + x % M)return x % M
}
书上习题5.6:求解同余方程组
{ x ≡ 12 ( m o d 25 ) , x ≡ 9 ( m o d 26 ) , x ≡ 23 ( m o d 27 ) , \begin{cases} x\equiv12\pmod{25}, \\ x\equiv 9\pmod{26}, \\ x\equiv 23\pmod{27}, \\ \end{cases} ⎩⎪⎨⎪⎧x≡12(mod25),x≡9(mod26),x≡23(mod27),
答案:14387。 测试结果:
console.log(CRT([[2, 3],[3, 5],[2, 7]
]))
result:
2 35 2
3 21 1
2 15 1
233mod105=23
23console.log(CRT([[12, 25],[9, 26],[23, 27]
]))
result:
12 702 13
9 675 25
23 650 14
470687mod17550=14387
14387
——End——
这篇关于中国剩余定理Chinese remainder theorem(CRT)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!