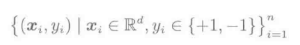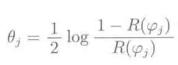有监督分类：集成分类（Bagging Boosting RandomForest）

本文主要是介绍有监督分类：集成分类（Bagging Boosting RandomForest），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.前言

集成学习（Ensemble），是指把性能较低的多种弱学习器，通过适当组合形成高性能的强学习器的方法。“三个臭皮匠顶个诸葛亮”这句谚语用来形容集成分类器最合适不过了。这几年，关于集成分类的研究一直是机器学习领域的一个热点问题。在这里，只分析了两个我比较熟悉的集成分类方法。

对多个弱学习器独立进行学习的Bagging学习法
对多个弱学习器依次进行学习的Boosting学习法

虽然目前集成学习的思维方式适用于回归、分类等各种类型的机器学习任务，但这里之谈分类问题。

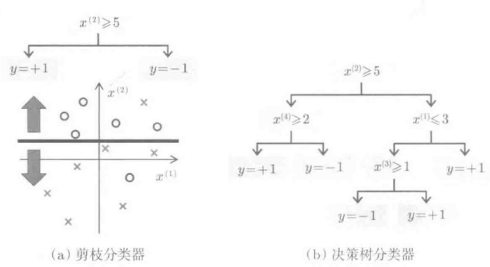
2.剪枝分类方法

剪枝分类是属于弱分类器的一种单纯分类器。剪枝分类是指，对于d次维的输入变量：

任意选定其中的一维，通过将其值与给定的与之相比较来进行分类的线性分类器。即以输入空间内的坐标轴于朝平面进行正交的方式对模式进行分类，原理如下所示：

剪枝分类器中的“枝”是从树上剪下来的枝节

剪枝分类器通过一层一层的积累形成树状结构成为决策树分类器

剪枝分类器的自由度很低，怎么都称不上是优秀的分类器，但是他确实具有计算成本低的优点。具体而言，对于n各训练样本，首先根据所选取的维度的数值进行分类。然后，对于i=1,...,n-1，计算顺序为i何i+1的训练样本在分类时的误差，使分类误差最小，从而决定分类边界。也就是说，剪枝分类器候补解最多只有n-1个，所以通过对所有可能的解进行分类误差的计算并确定最小值，由此就可以得到最终的解。

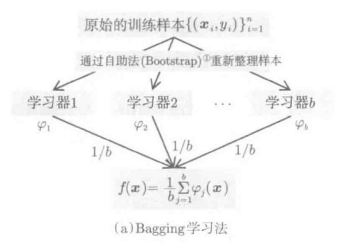
3.Bagging学习法

Bagging = Bootstrap Aggregation

Bootstrap是指从n个训练样本中随机选取n个，允许重复，生成与原始的训练样本集有些许差异的样本集的方法。

Aggregation：聚集、集成。

在Bagging学习中，首先经过由自助生成虚拟的训练样本，并对这些样本进行学习，然后，反反复复这一过程，对得到的多个分类器的输出求平均值。具体算法流程如下图所示：

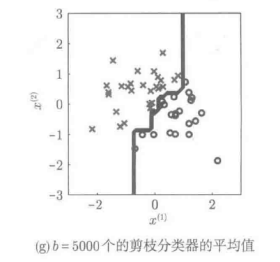
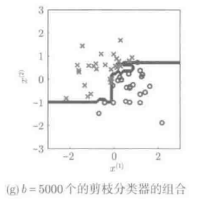
通过上述方法，就可以从大量略有不同的训练样本集合，得到多个稍微不同的弱分类器，然后在对这些分类器加以统合，就可以得到稳定可靠的分类器。

下图展示的是，利用剪枝分类器进行Bagging的实例：

对剪枝分类器进行Bagging学习实例（5000）

Bagging学习中，通过单一的剪枝分类器的组合，可以获得复杂的分类边界。

一般而言，像剪枝分类器这样非常单一的弱分类器，对其进行学习很少会发生过拟合现象，因此Bagging学习的重复次数设置为较大值是比较好的选择。在这种情况下，因为多个分类器的学习是个并列的过程，因此可以使用多台计算机并行处理，会使计算效率得到巨大的提升。

剪枝分类器不断地生长、积累，形成多层级的模型，该模型就称为“决策器分类器”（如山所述）。对决策树分类器进行Bagging学习的时候，通过随机选择输入变量中某个维度进行学习，可以大幅度提高分类器的性能，这种方法有个更熟悉的名字：随机森林学习。

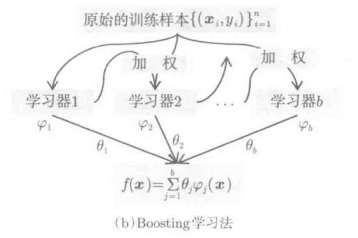
4.Boosting学习法

Boosting学习，首先使用一个原始的学习算法，对训练样本：

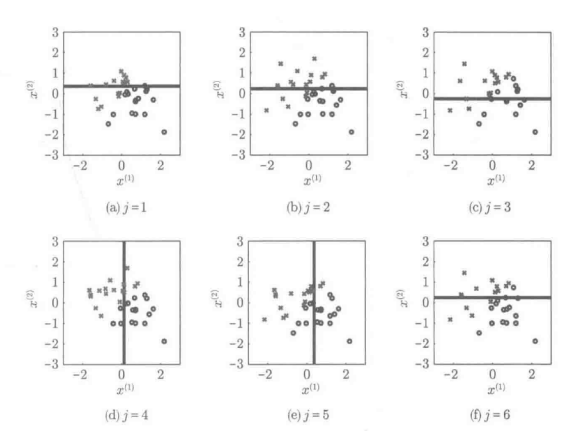
进行普通分类器学习。如果这个原始的学习算法性能不高，就不能对所有训练样本进行正确的分类。因此，对于不能正确分类的困难样本，就加大其权重（反之，对于能正确分类的简单样本则减少其权重），再重新进行学习。这样再次得到的分类器，对原本没能正确分类的样本，应该也能在一定程度上进行正确的分类了。然后，在循环多次进行加权学习，慢慢地就可以对所有训练样本都进行正确的分类了。

然而另一方面，在进行加权过程中，最开始就能够正常分类的样本的权重会慢慢变小，有可能造成建大的样本反而不能正确分类的情况。因此，Boosting学习应该边学习边更新样本的权重，并把学习过程中得到的所有分类器放在一起，对其可信度进行平均后训练得到强分类器。

样本的加权方法多种多样，最为标准的就是AdaBoost算法，如下图所示：

Adaboosting学习算法

可以分析一下决定分类器的权重Θj的式子：

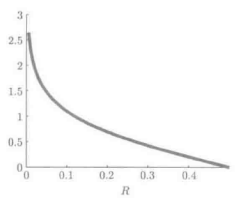
根据该式，加权的误分类率R()越小，其权重Θ就越大，如下图所示：

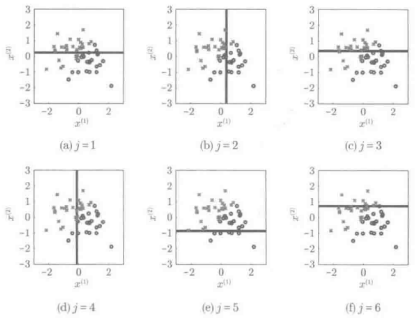
Adaboosting学习中，基于加权误分类率R来确定分类器的权重Θ

下面是对剪枝分类器进行Adaboosting学习的一个例子：

对剪枝分类器进行Adaboosting学习（b=50000）