4. 无向图的各连通分支

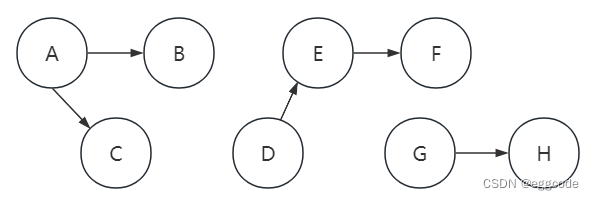
本文主要是介绍4. 无向图的各连通分支，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

求解无向图的各连通分支

输入：

第一行为图的节点数n（节点编号0至n-1，0<n<=10）
从第二行开始列出图的边，-1表示输入结束

输出：
输出每个连通分支的广度优先搜索序列（从连通分支的最小编号开始），不同分支以最小编号递增顺序列出

sample：
input:
8
0 5
5 2
4 5
5 6
6 2
3 7
-1

output：
0-5-2-4-6
1
3-7

C++代码

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>using namespace std;// 广度优先搜索函数
void bfs(int start, vector<bool>& visited, const vector<vector<int>>& adjList) {queue<int> q;q.push(start);visited[start] = true;while (!q.empty()) {int current = q.front();q.pop();cout << current;  // 输出当前节点// 获取当前节点的所有相邻节点// 如果相邻节点未被访问过，则标记为已访问并加入队列for (int adj : adjList[current]) {if (!visited[adj]) {visited[adj] = true;q.push(adj);}}if (q.size()>0) cout << '-';}
}int main() {int n;cin >> n;  // 读取节点数vector<vector<int>> adjList(n);  // 邻接表vector<bool> visited(n, false);  // 访问标记int u, v;while (true) {cin >> u;if (u == -1) break;cin >> v;adjList[u].push_back(v);  // 添加边adjList[v].push_back(u);  // 假设图是无向图，添加另一条边}// 对所有节点的邻接列表进行排序，以确保按节点编号升序搜索for (auto& edges : adjList) {sort(edges.begin(), edges.end());}// 对每个连通分支执行广度优先搜索for (int i = 0; i < n; ++i) {if (!visited[i]) {bfs(i, visited, adjList);  // 执行广度优先搜索cout << endl;}}return 0;
}

这篇关于4. 无向图的各连通分支的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---