本文主要是介绍matlab 列主元 三角分解法 解线性方程组 数值分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
%MtriangleDecomposition
%带列主元法的三角分解%input输入矩阵,包括系数和参数
%inputC 用于分解LU矩阵的合成矩阵
%oringinData保留的初始矩阵
%output 输出答案,对应X的各个值
%Toutput:修正顺序后的答案,对应输入数据的X顺序
%rememberdet:行列变化中介值
%remember:行列变化记录矩阵
%xnum,ynum 输入矩阵的尺寸
%Lneed 消元中,主式需要乘的变量
%keepnum 保留小数位数
%contrastFrom(各个多项式的误差)
%deltanum:矩阵中变化的最大值
%Ldet:分解出来的下矩阵
%Udet:分解出来的上矩阵%%注意,元素中不能有为零的数
clear all%启用模块化后需要注释该句input=[0,2,0,1,0;2,2,3,2,-2;4,-3,0,1,-7;6,1,-6,-5,6];%输入矩阵
oringinData=input;error1='the condition are not meet for using this algorithm' ;%format short%设置精度 short为精确到小数点后3位 数值型 roundn(A,3)保留3位小数keepnum=-20;%设置保留n位小数,记得加负号表示小数位
[ynum,xnum]=size(input);%获取输入矩阵大小Ldet=zeros(ynum);
Udet=zeros(ynum);%创建LU的背景矩阵
inputC=input;
[Ldet,Udet]=lu(input);%开始解方程组
%回代
for i=1:ynum%这里计算出结果output(ynum+1-i,1)=roundn(Udet(ynum+1-i,xnum),keepnum)/roundn(Udet(ynum+1-i,xnum-i),keepnum)%output为输出结果for j=i+1:ynum%回代结果到多项式中,将其他值消除if i<ynumUdet(ynum+1-j,xnum)=roundn(Udet(ynum+1-j,xnum),keepnum)-roundn(Udet(ynum+1-j,xnum-i)*output(ynum+1-i,1),keepnum);Udet(ynum+1-j,xnum-i)=0;endendend

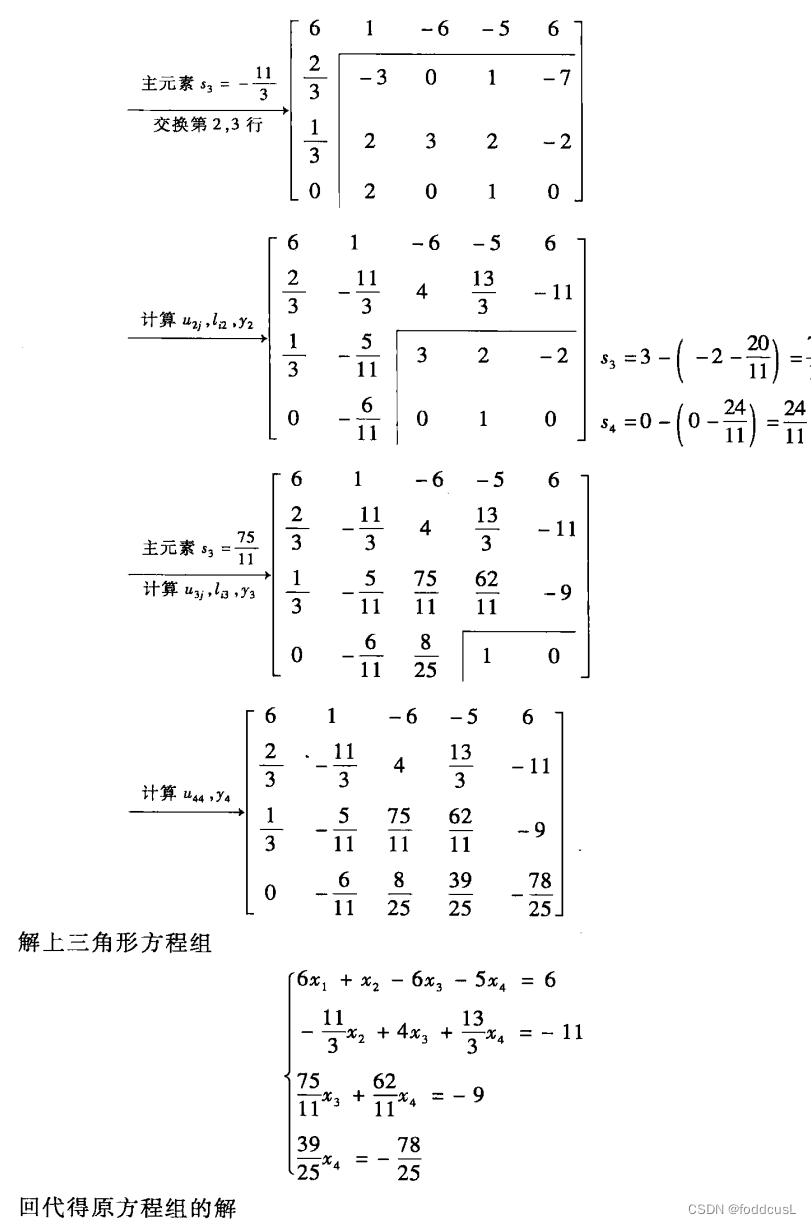
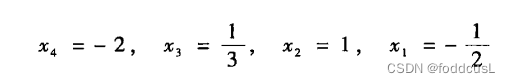
这篇关于matlab 列主元 三角分解法 解线性方程组 数值分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






