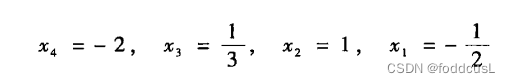以下是一个使用高斯消元法和列主元消去法求解线性方程组的示例： 假设我们要解决以下线性方程组： 4x + 2y + z = 8 -2x + y - 3z = -11 3x - 2y + 4z = 10 首先，我们可以将该线性方程组表示为增广矩阵的形式： [4 2 1 | 8] [-2 1 -3 | -11] [3 -2 4 | 10] 使用高斯消元法，我们可以进行以下操作： 将第一个方程

L: lower triangular 下三角 U: upper triangular 上三角 LU 分解，顾名思义，为 把一个 矩阵 分成 一个下三角矩阵 乘上一个上三角矩阵的形式。 Example 为什么可以这样 几个基本的初等行变换，可以自己验算一下，等式的左边与右边是相等的 用上面这几个等式，重新看一下 第一个例子， 对A进行了三次行变换，得到上三角矩阵U， 两边同时左乘初等

%MtriangleDecomposition%带列主元法的三角分解%input输入矩阵，包括系数和参数%inputC 用于分解LU矩阵的合成矩阵%oringinData保留的初始矩阵%output 输出答案，对应X的各个值%Toutput：修正顺序后的答案，对应输入数据的X顺序%rememberdet：行列变化中介值%remember：行列变化记录矩阵%xnum,ynum 输入矩