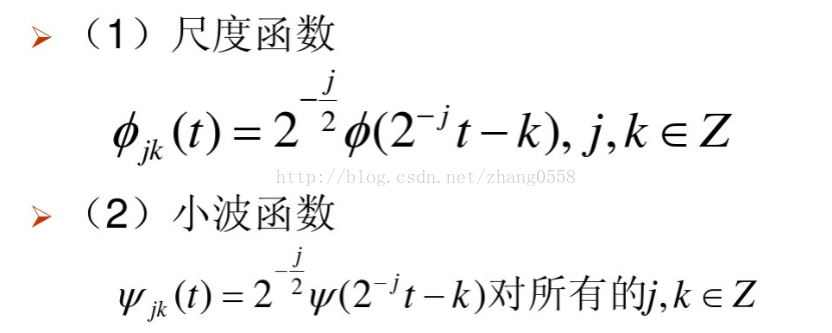小波变换的前因后果（二）

上一章介绍了为什么要小波变换，是篇启发文。分别是解决傅里叶对局部信息不敏感、对时刻时频分析能力欠缺，衍生出来小波变换。又简单知道了小波变换的公式：尺度因子决定小波伸缩(频率)、时移因子决定滑动平移。下面开始详细介绍什么是小波变换，即CWT、DWT两种形式。

一、小波变换

小波变换是一种信号的时间——尺度（时间——频率）分析方法，它具有多分辨分析的特点，而且在时频两域都具有表征信号局部特征的能力，是一种窗口大小固定不变但其形状可改变，时间窗和频率窗都可以改变的时频局部化分析方法。即在低频部分具有较低的时间分辨率和较高的频率分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，很适合于分析非平稳的信号和提取信号的局部特征，所以小波变换被誉为分析处理信号的显微镜。

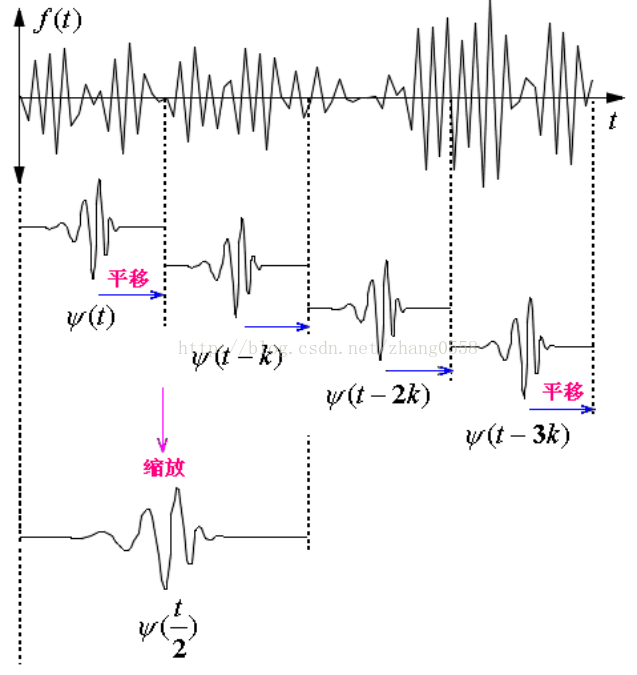
傅里叶是将信号分解成一系列不同频率的正余弦函数的叠加，同样小波变换是将信号分解为一系列的小波函数的叠加(或者说不同尺度、时间的小波函数拟合)，而这些小波函数都是一个母小波经过平移和尺度伸缩得来的，如下图。

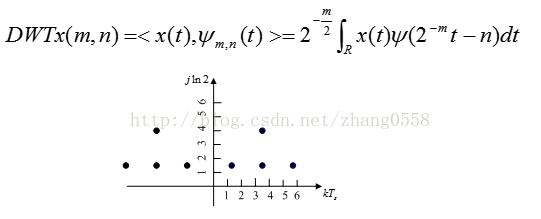
小波变换常见的形式有连续小波变换(CWT)、离散小波变换(DWT)等。连续小波变换是在尺度基础上连续变换的，做信号的小波分析得到的是幅值，a时间的三维图，对应的a值所截得的曲线即为该尺度的小波图形。而离散小波变换常用的是二进小波变换，对尺度和时间进行离散化处理。

1、CWT连续小波变换

CWT步骤：

（1）首先选择一个小波基函数，固定一个尺度因子，将它与信号的初始段进行比较；

（2）通过CWT的计算公式计算小波系数（反映了当前尺度下的小波与所对应的信号段的相似程度）；

（3）改变平移因子，使小波沿时间轴位移，重复上述两个步骤完成一次分析；

（4）增加尺度因子，重复上述三个步骤进行第二次分析；

（5）循环执行上述四个步骤，直到满足分析要求为止。

连续小波变换是在尺度基础上连续变换的，做信号的小波分析得到的是幅值，a时间的三维图，对应的a值所截得的曲线即为该尺度的小波图形。而集散小波变换常用的是二进小波变换。

但是，cwt的结果都相当于DWT中的细节信息（即所谓DWT中的高频信息。虽然越向后频率越低，有时已不能用“高频”来形容了，但这时的高频是相对概念，是相对于同阶逼近信息还是高的），只是其尺度是连续的尺度越大频率越低，一直低下去。

morlet等小波只能做CWT，有些是因为没法儿构造尺度函数，有些是根本就没有逆变换（只有满足某些条件，CWT才存在逆变换，这与小波基有关），有些是如何离散化也不能构成正交或双正交基，甚至按照二进制的离散化不能构成紧支的框架，所以它们通常不能做DWT，也就没有逆变换、重构一说了。

2、DWT离散小波变换

离散小波变换DWT对尺度参数按幂级数进行离散化处理，对时间进行均匀离散化取值如二进制离散化尺度时间为2,4,6,8...2n（要求采样率满足尼奎斯特采样定理），常用于信号的多分辨分析、信号分解重构。

多分辨分析也称为多尺度分析，是建立在函数空间概念上的理论。在不同的尺度和时间下，分别构造了尺度函数向量组合小波函数向量组，也即是尺度函数向量空间V与小波函数向量空间W，在一定层次下，信号在尺度空间做卷积所得到的是信号的近似、低频信息，信号在小波空间W做卷积所得到的是信号的细节、高频信息。(注意：尺度与分解层数不是一个概念，尺度与频率成反比的，分解层数是对频率的范围进行一定的划分)。

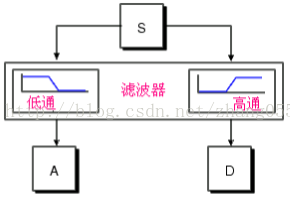
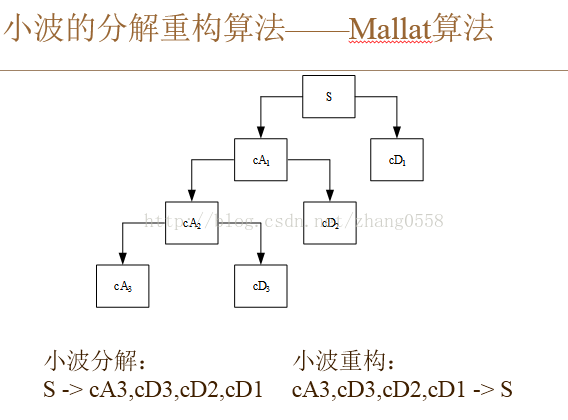
在多分辨分析中，如正交小波变换可以等效为一组镜像滤波的过程，即信号通过一个分解高通滤波器和分解低通滤波器，高通自然的滤波器输出对应的信号的高频分量部分，称为细节分量，低通滤波器输出对应了信号的相对较低的频率分量部分，称为近似分量。对应的快速算法称为Mallat算法。（后面章节就讲述） 

小波分解重构过程（其中CA为低频信息、近似分量，CD为高频、细节分量）：

后见小波变换的前因后果(三)