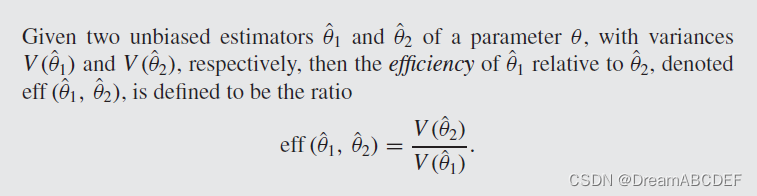点估计的性质和估计方法 Properties of Point Estimators and Methods of Estimation

本文主要是介绍点估计的性质和估计方法 Properties of Point Estimators and Methods of Estimation，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

9.1 Introduction

9.2 Relative Efficiency

定义：

9.3 Consistency

定义：

定理：

9.4 Sufficiency

Sufficient 定义：

Likelihood 定义：

定理：

9.5 The Rao–Blackwell Theorem and Minimum-Variance Unbiased Estimation

Rao-Blackwell 定义：

MVUE 定义：

例题：

9.6 The Method of Moments

定义：

例题：

总结：

9.7 The Method of Maximum Likelihood

定义：

9.8 Some Large-Sample Properties of Maximum-Likelihood Estimators (Optional)

9.1 Introduction
9.2 Relative Efficiency
- 定义：
9.3 Consistency
- 定义：
- 定理：
9.4 Sufficiency
- Sufficient 定义：
- Likelihood 定义：
- 定理：
9.5 The Rao–Blackwell Theorem and Minimum-Variance Unbiased Estimation
- Rao-Blackwell 定义：
  - 提供了一个 sufficient statistic 和 unbiased estimator 之间的连接
  - 一个是θ的非偏估计，然后U是的sufficient statistic，那么U的一个函数也是θ的非偏估计，且U的方差更小。因此我们可以通过这个定理得到θ的更优非偏估计。
    - 具体步骤：1. 求出sufficient statistic U，2. 寻找h(U)，使得E[h(U)]=θ。
- MVUE 定义：
  - Minimum-variance unbiased estimator 最小方差非偏估计
- 例题：
  - Y1, ..., Yn是伯努利变量，已知P(Yi=1)=p, P(y1=0)=1-p。求p的MVUE。
  - 解：
    - 1. 求sufficient statistic U： $L(y_1, ..., y_n|p)=p(y_1)...p(y_2)=p^{y_1}(1-p)^{1-y_1}...p^{y_n}(1-p)^{1-y_n}=p^{\sum y_i}(1-p)^{n-\sum y_i} \cdot 1=g(\sum y_i, p) \cdot h(y_1, ..., y_n)\\ U=\sum y_i$
    - 2. $E(U)=E(\sum y_i)=np \rightarrow E(U/n)=E(\bar{Y})=p$
    - 所以 $\bar{Y}$ 是p的MVUE。
9.6 The Method of Moments
- 思想很简单，样本的秩应该是总体的秩的一个很好的估计。
  - 随机变量的第k个秩： $\mu'_k=E(Y^k)$
  - 对应的第k个样本秩： $m'_k=\frac{1}{n}\sum_{i=1}^n Y_i^k$
- 定义：
- 例题：
  - Y1, ..., Yn取自（0，θ）区间内的均分分布。θ未知，需要估计θ。
    - $\mu'_1=\mu=\frac{0+\theta}{2}=\frac{\theta}{2}$
    - $m'_1=\frac{1}{n}\sum_{i=1}^nY_i=\bar{Y}$
    - $\mu'_1=m'_1 \rightarrow \frac{\theta}{2}=\bar{Y} \rightarrow \hat{\theta}=2\bar{Y}$
- 总结：
  - 很方便，计算出的估计都是consistent的。但是这些估计通常不是sufficient statistic的函数，所以不是很efficient（会比别的方法算出来的估计拥有更大的方差），有的时候甚至是biased的。
9.7 The Method of Maximum Likelihood
- 定义：
- 一个很好的贴子：🔗
9.8 Some Large-Sample Properties of Maximum-Likelihood Estimators (Optional)