因果推断（四）——后门调整、前门调整、逆概率加权

        在因果推断（三）中，我们介绍了干预的相关概念，在本文中，我们对一些方法进行介绍，这些方法可用于利用干预分析变量之间的因果关系。

在因果推断（三）中，我们得出了调整公式，如上式。假设PA为A节点的所有父节点的集合，则上

式可以修改为

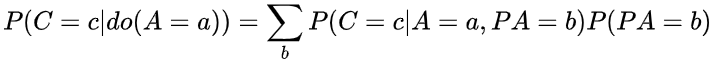
其中b为PA所有可能的取值

后门调整

    回顾后门准则的定义：对于X到Y的路径中，如果Z集合中的节点不是X的后代节点，并且以Z为条件会阻断所有X和Y之间的后门路径，则Z满足（X,Y）的后门准则。如果B满足后门准则，则后门调整公式就是我们在前面所推出的调整公式。通过该公式可以计算出C和A之间的因果关系。

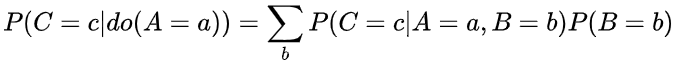
前门调整

• 前门准则的定义

• D阻断了A到C之间的所有路径

• D到C之间的后门路径都被A阻断

• A到D之间没有未阻断的路径

则D满足A到C的前门准则。

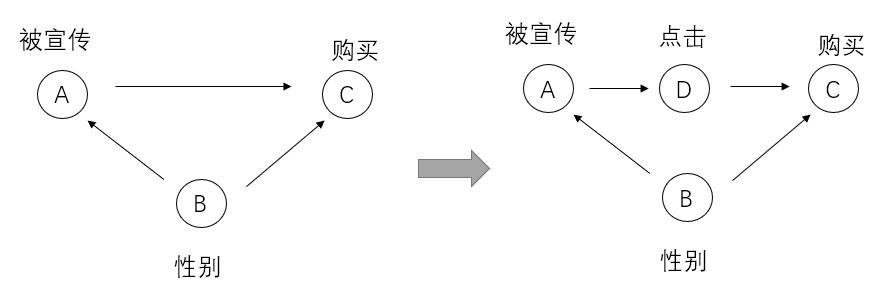
    在因果推断（三）的辛普森悖论中我们用到了小夏开店的例子，其因果图为上图的左子图，现在我们将其修改为右子图。多了一个点击的情况。还是沿用小夏开店的例子，假设我们需要分析被宣传（A）和购买（C）之间的因果关系，那么我们可能会想到后门调整，用到上述的调整公式，但是如果此处我们无法获取性别（B）的相关数据，此时我们就无法采用后门调整了，这里我们可以采用前门调整。

此处我们可以用过A->D，D->C这样一个前向的过程来分析因果关系。

• A对D的因果效应可以表示为

  

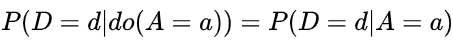
  ，因为这条路径不存在混杂，所以不需要考虑去除混杂的情况。

• D->C的因果效应分析中，存在混杂（A，B）。由于B未知，所以这里采用A来去除混杂，公式如下就是后门调整。

    这里给出混杂的定义，具体例子可以看因果推断（二）。定义：1. E与D相关，2. 以D为条件时，E与C相关，3. E不在D到C的因果关系路径中。则称E为混杂因子。

    得到了A->D和D->C的因果效应后，我们通过前门调整来分析A->C的因果效应。

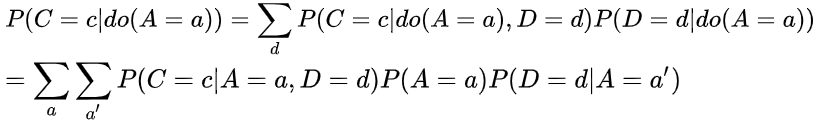
这里可以看成是A->D和D->C这两个过程在不同a的值时的因果效应的乘积

 逆概率加权

仍然以小夏开店为例，以上图的左子图为例

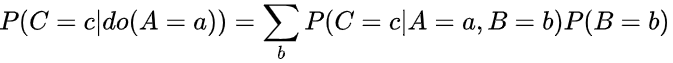
左右同乘P(B|A)得到：

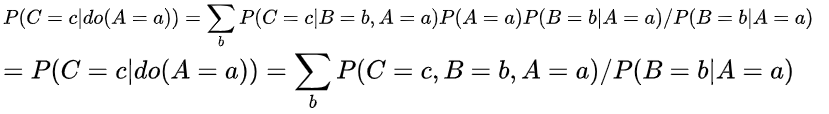
除以这个条件概率，相当于去除了性别（B）导致的偏差，也就相当于去除了混杂，不过这边我们需要知道a,b,c的全概率。

    逆概率加权也是在推荐系统中去除数据偏差的热门方法，后续我们会进行介绍。

 更多内容可以关注我的公众号“秋枫学习笔记”