《Evolving Neural Networks through Augmenting Topologies》by Kenneth O. Stanley and Risto Miikkulainen

 Abstract

要解决的问题：网络的结构和参数一起进化

优势：①提出了一种在不同结构之间交叉的方法；②通过种族（speciation）来保障种群的创新性；③从一个最小的拓扑结构进行进化。

实验：①通过对比实验证明，在加强学习的任务上，增长性的结构比固定结构性能更好；②通过剪切实验证明NEAT算法的各个部分不可或缺。

贡献：①证明GA可以同时优化和复杂化（这里的复杂化应该指的是多样化）解。

 

 

介绍

①神经进化被证明有利于加强学习（Gomez and Miikkulainen 1999; Gruau et al. 1996; Moriarty and Miikkulainen 1997; Potter et al. 1995; Whitley et al. 1993）

原因：父代信息可以有效保存在基因中，因此更有益于解决非马尔科夫问题（需要了解过去的状态来做决策的问题）。

②传统的NE是在一开始就选择了一个固定的拓扑结构（一个输入层和一个输出层，中间一个隐藏层，全连接），然后使用算法优化结构中的参数。但是结果的好坏是和网络的结构也是有关的。

③本篇文章的贡献：证明结构和参数的进化都可以加强神经进化算法的性能。

④解决的问题：1，拓扑结构能有意义地交叉；2，拓扑结构能在优化前不被换掉；3，在进化的过程中最小化结构。

 

 

背景

TWEANN Encoding

TWEANN 全称Topology and Weight Evolving Artificial Neural Network，指结构和参数共同进化的神经网络。

Binary Encoding

传统的编码方式是将每一个节点编码为基因上的一个染色体，假设有n个节点，然后节点之间的连接就用一个n^2的矩阵表示。这个方法的缺陷在于需要人为确定最大节点的值，不能自由地拓展节点的数量。

Graph Encoding

使用更方便的图编码来表示一个网络。例如Pujol and Poli (1997)使用两个染色体来表示网络，一个表示网络的结构，一个线性表示连接。图交叉则使用网格表示，点交叉则使用线性表示。

Non-mating

由于网络结构的交叉会频繁导致性能的变化，因此，一些人放弃了交叉。也有论文GNARL证明TWEANN问题不需要经过交叉。

Indirect Encoding

间接编码是指基因不能直接表示，但是可以通过基因推导出来。

Competing Conventions

Competing Conventions Problem，也称Permutations Problem，是指有多种方式来表示一个神经网络的参数。 

两个染色体在交换后会失去基因信息，例如论文中（A，B，C）和（C，B，A）交叉后的子代。

Protecting Innovatin with Speciationo

一个新的结构形成之后需要经过几代的演化才可以产生好的参数，因此新的结构需要保护。

方案：结构相同的个体划分为同一个物种，同一个物种内进化。

Initial Populations and Topological Innovation

随机初始缺点：①输入输出没有连接；②不利于寻找最简单结构的解，因为会生成许多无用的节点。

最小化网络结构：①将网络的大小加入fitness function。缺点：无法定义网络大小在fitness function中的比例，而且有些问题的解决确实需要大的网络。②从最小的网络开始，如果添加一个节点是有利于找到解的，则增加。

当前TWEANN问题没有从最小网络开始的原因是，最小网络一开始时一个最简单的全连接，在演化的过程中没办法产生复杂的新结构，但是，加入物种这一个概念之后，可以通过物种之间的交叉变异来产生新的结构。

An Integrated Scheme

NEAT就是将以上方法综合在一起

 

NeuroEvolution of Augmenting Topologies (NEAT)

Genetic Encoding

connection genes：每个基因表示两个节点之间的连接

node genes：包含输入节点，隐藏节点，输出节点

connection gene：包含入节点，出节点，节点的参数，是否启用，创新号。

mutation：①mutate add connection 在两个未连接的节点之间添加连接；②mutate add node：在一个连接之间添加一个节点，新节点到旧out节点之间的参数继承旧连接，旧in节点到新节点之间的参数设为1

Tracking Genes through Historical Markings

innovation number的产生：当连接7中间添加一个新的node后，一个连接被切断成两个新的连接，然后命名为8,9。这样产生的innovation number在交叉变异后保持不变。

防止重复innovation number号的产生：如果一个相同的结构经过多次变异后会产生相同的结构，但是会有多个不同的innovation number，为了防止这种情况产生，通过维持一个list of the innovations occurred in the current generation，记录当前种群发生变异。

交叉：通过对应innovation number，然后随机从父代中选择相对应的基因，组成新的基因组。

Protecting Innovation through Speciation

通过把类似的结构划分为一个物种，然后相同的结构在同一个物种之间相互进化。

计算两个网络之间的距离：

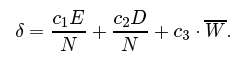
E：两个网络之间节点的数量差

D：两个网络之间innovation number不对应的数量

W：两个网络之间参数的平均值的差

c1，c2，c3是调节权重的参数

将个体根据距离划分为不同的物种：

个体g与每个物种中的代表个体进行比较，距离小于compatibility threshold Æ，则加入物种，若都不相符，则产生新的物种

物种之间的交流：explicit fitness sharing

为了防止某一物种拓展太大，即使物种内的个体都比较优良。需要调整fitness

子物种的大小由fi决定

Minimizing Dimensionality through Incremental Growth from Minimal Structure

NEAT的初始网络从一个最简单的，只包含输入层和输出层的全连接网络，然后在网络上添加节点，添加连接，每次添加的结构都是有用的，最后得到的网络中将没有多余的无用节点，因此是最简网络。

 

Performance Evaluations

解决的问题

①NEAT能够使网络的必要结构得到进化吗？

通过解决XOR问题来回答这个问题

②NEAT的结果是不是能够比其他的算法要优？

通过在cart-pole balance problem上试验来回答这个问题

Parameter Settings

试验的参数设置可以应用到任何问题，因为最终的问题是要形成一个有效的神经网络。而神经网络的权重与超参数是在进化的过程中形成的。

如果一个物种在15代后没有得到进化，则陷入停滞状态。

基因有80%的概率mutate，其中90%概率抖动，10%的几率被赋予一个新的随机值

25%的子代是没有交叉过而只变异产生的

交配的概率是0.001

大种群产生新连接的概率会比小种群的概率高，因为大种群可以容纳更多物种

Verification: Evolving XORs

在结构的扩展过程中，会存在以下问题:

①添加一个新的节点会对结构造成负面影响

②一个局部最优解可能会主导种群

③变化的机构可能导致某些好的连接的参数被弃用

结果的评价标准 fitness function:

(4-sum（每个output与正确结果output的距离))^2

Pole Balancing Comparisons

Ev. Programming：仅仅依靠参数的变异

Conventional NE：使用交叉变异

SANE：固定的网络结构，维护neurons种群和network blueprints种群，两个种群共同组成网络

ESP：SANE的改进，使用一个种群来表示网络不同的隐藏层结构

Double Pole Balancing with Velocities

评判的标准：在100000步内保持杆平衡

杆平衡的标准：角度保持在-36~36度之间

Double Pole Balancing Without Velocities

标准：

①防止杆只是无意义地抖动，采用两个fitness function的加权组合

②最后的结果需要在625种随机初始状态测试中成功200组

 

 

Analysis of NEAT

通过对NEAT各个部分的剔除来比较NEAT的性能