本文主要是介绍机器学习 :李宏毅:线性回归 梯度下降:(goodness of function),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
机器学习:线性回归 笔记记录
机器学习的三步走
1.设计函数模型(构造函数)
设计线性模型: 
x为视频所说的10组数据
w,b为所求的值
y^表示的是通过所构造的函数得到的预测值
2.判断函数的好坏
梯度下降:(goodness of function)
训练数据为十组
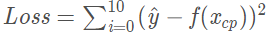
y^ 为预测值,f(x)为10组数据的真实值
Loss越小越好,Loss就是我们判断我们设计的函数模型好坏的工具
3. 选择最好的函数
由于学习过高数知识,我们可以知道 函数的极大值或者极小值存在于该函数的导数等于零的位置。因此我们对Loss 进行偏微分 的到Loss的最小值

接下来我们要使用梯度下降算法:
首先关于李宏毅视频中所讲的初始值的w,b都是随机初始化。

如图所示,进行迭代10000次
η :学习率,一般来讲,在导数固定的情况下,学习率越大,w或b变化也就越大。一般学习率的值为(0.001~ 0.1 ~1)(个人理解)
对于学习速率的理解可以参考视频李宏毅老师所讲。
寻找最小值的过程不是一帆风顺的,我们有可能会遇到学习很慢(导数接近0)、鞍点(导数为0,但是周围还是有下降空间)、局部最小值(导数为0,但是得到的结果不是整体最小值,而是局部最小值)等问题。(暂时略过)
将得到的w,b放如所构造的函数中,和原始值进行比较(做差值)
以上是我个人认为,梯度下降的难理解的地方,图片来源均为哔哩哔哩李宏毅机器学。
这篇关于机器学习 :李宏毅:线性回归 梯度下降:(goodness of function)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





