LUNAR：基于图神经网络统一局部异常检测算法

AAAI 2022上的论文《LUNAR: Unifying Local Outlier Detection Methods via Graph Neural Networks》提出了一种基于图神经网络进行异常检测的框架，统一了常见局部异常检测方法的同时，也一定程度上解决了局部异常检测算法超参数无法学习，难于优化的问题。

研究动机

提到异常检测算法，最常见的思路往往是基于局部近邻距离来判断样本点是否为异常点。这种局部异常检测的方法，比如LOF，DBSCAN，KNN，在基于特征的非结构化的数据集上往往有不错的表现。但是，这些算法普遍缺乏可学习的参数，这使得他们难以适应不同的数据集。同时由于异常检测算法往往是无监督学习，上述算法的超参数，比如KNN和LOF中k值的选取，很难基于表现进行调优，而这些超参数的影响又很大。因此，现有局部异常检测的方法很难在不同数据集中取得同样稳定的表现。

基于神经网络的异常检测方法，由于有标注的异常点数据有限以及其主要是针对如图像数据的高维度结构化数据集的原因，在基于特征的低结构化数据集上的表现始终不尽人意。目前缺乏一种在这一类数据的异常检测中表现优异且稳定的，具有一定可学习参数的算法模型。

解决的问题

作者首先提出了目前的局部异常检测算法在图神经网络(Graph Neural Networks)上的统一框架。之后，基于这个图神经网络的框架，作者提出了LUNAR(Learnable Unified Neighbourhood-based Anomaly Ranking)。凭借更多的可训练参数，LUNAR在多个数据集中的灵活度与适应性要强于现有的局部异常检测算法。在性能上和健壮性上，LUNAR也比传统的异常检测算法以及基于神经网络的异常检测算法表现更好。

所提的方法

引入图神经网络，将现有局部异常检测算法与图模型进行结合，从而得到一个统一的框架。

图神经网络(GNNs)

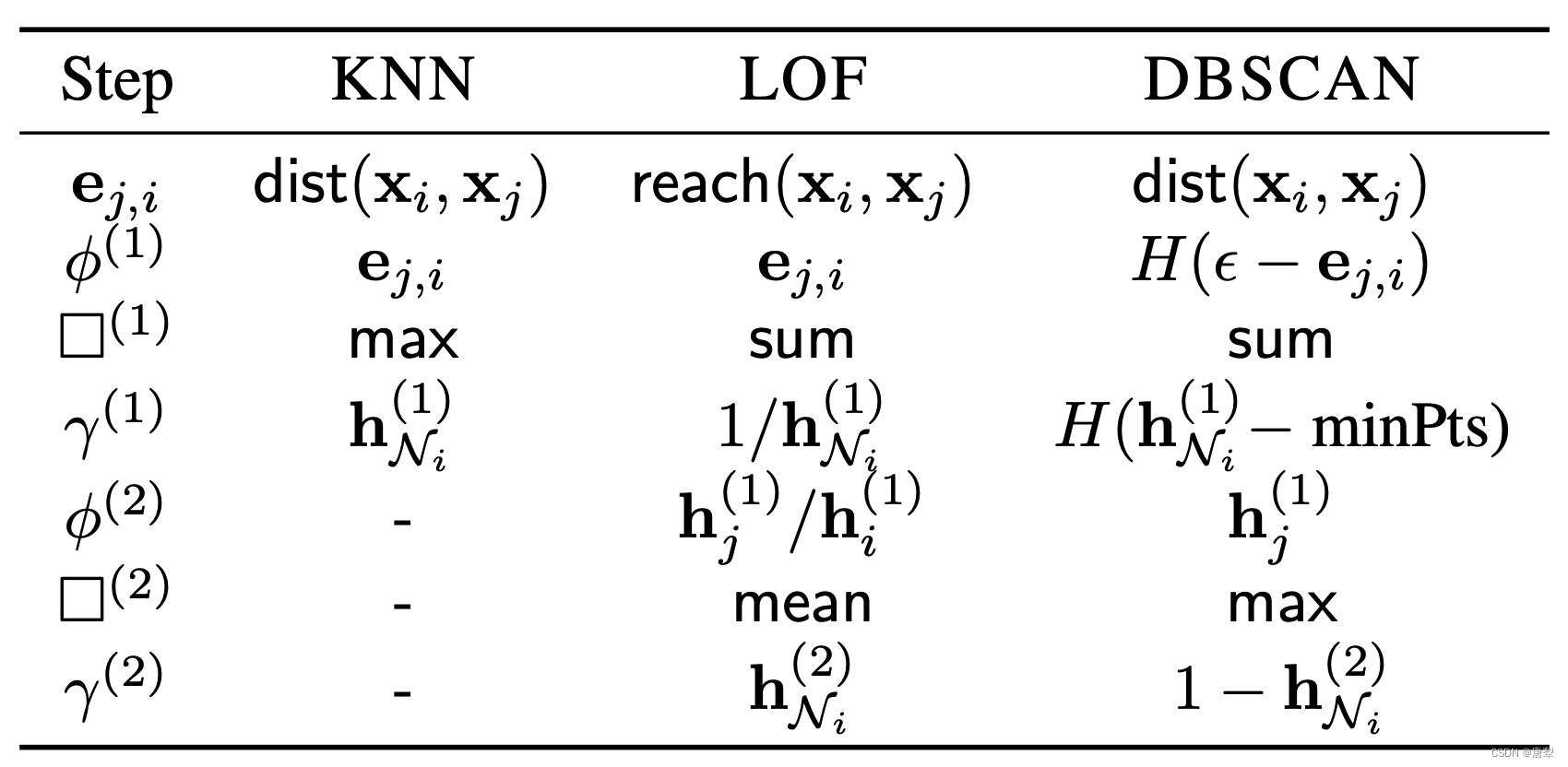
图$G(V,E)$由节点集$V$和边集$E$构成。两个相邻节点$i,j\in V$，其连接的边记作$(j,i)\in E$。边可以是无向的，信息在无向边上可以双向流动。边也可以是有向的，即信息只能由源节点流向目标节点。节点和边都可以具有特征向量，节点$i$的特征向量记作$x_i$，边$(j,i)$的特征向量记做$(e_{j,i})$。

每个节点都具有一个节点向量。依靠一个消息传递方案，GNNs可以基于神经网络为每个节点进行分类。消息传递方案由消息，聚合，和更新三部分构成。消息函数$\varphi$决定了从每个相邻节点发送至当前节点的信息。聚合函数$\square$将这些相邻节点传来的信息汇总为一个信息，比较常见的方式是使用平均或者最大池化。更新函数$\gamma$使用聚合后的信息为当前节点更新其向量。在一个GNN的第k层，节点的向量值计算可以表示为：
$${\text{h}}_{{\mathcal{N}}_i}^{(k)}={\square }_{j\in {\mathcal{N}}_i}{\varphi }^{(k)}({\text{h}}_i^{(k-1)},{\text{h}}_j^{(k-1)},{\text{e}}_{j,i})$$
$${\text{h}}_i^{(k)}={\gamma }^{(k)}({\text{h}}_i^{(k-1)},{\text{h}}_{{\mathcal{N}}_i}^{(k)})$$
其中${\text{h}}_i^{(0)}={\text{x}}_i$，${\mathcal{N}}_i$是节点$i$的相邻节点集合，${\text{h}}_{{\mathcal{N}}_i}^{(k)}$是相邻节点传来的消息的聚合结果。

问题定义

假设我们有$m$个训练样本${\text{x}}_1^{(train)},...,{\text{x}}_m^{(train)}\in {\mathbb{R}}^d$以及$n$个测试样本${\text{x}}_1^{(test)},...,{\text{x}}_n^{(test)}\in {\mathbb{R}}^d$，每个样本都可能是正常的或异常的。算法为每一个测试样本${\text{x}}_i^{(test)}$输出一个异常分$s({\text{x}}_i^{(test)})$，分数高意味着其为异常值，分数低则为正常值。局部异常检测的算法可以被理解为，如何将${\text{x}}_i^{(test)}$到其最近样本的距离用于计算其异常分。

统一框架

局部异常检测的方法是从邻近样本点收集信息，计算出一个统计量，然后根据这个统计量来判断当前样本点是否为异常点。下面以KNN为例，将这一过程结合到GNNs的消息传递框架中。

KNN可以被认为是在一个有向图中，每个节点$i$最近的$k$个近邻节点$j\in N_i$依次与其有一条有向边$(j,i)$，由邻近节点$j$向当前节点$i$传输信息。边的权重$e_{j,i}$等于有向边$(j,i)$的边长，即：
$${\text{e}}_{j,i}=\{\begin{array}{rlr}& \text{dist}({\text{x}}_i,{\text{x}}_j)& \text{if}j\in {\mathcal{N}}_i\\ & 0& \text{otherwise}\end{array}$$
由于$j\in N_i\nRightarrow i\in N_j$，沿有向边$(j,i)$的信息流仅能由源节点$j$发送至目标节点$i$。在这样的图中，KNN可以被等效为以下消息，聚合，更新三部分：

消息：
$${\varphi }^{(1)}:={\text{e}}_{j,i}$$
聚合：
$${\text{h}}_{N_i}^{(1)}:=\underset{j\in N_i}{\max }{\varphi }^{(1)}$$
更新：
$${\gamma }^{(1)}={\text{h}}_{N_i}^{(1)}$$
同样的，使用两层消息传递就可以获得LOF和DBSCAN在图模型上的等效。

可学习的重要性

论文中的实验表明，在选取不同的k值时，LOF的变化相对较大，而LUNAR则有更为健壮的表现。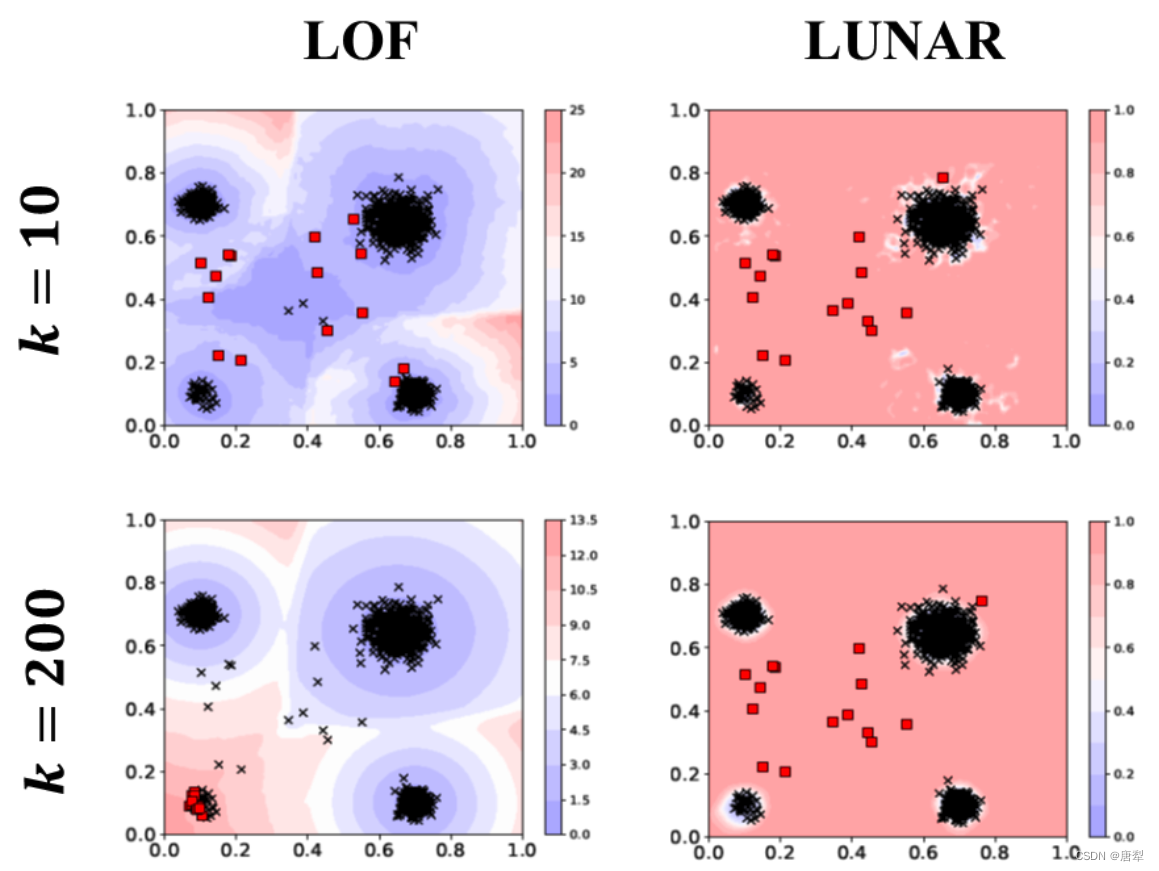

LUNAR

LUNAR首先为数据集构建一个k-NN图，将数据集中的每个样本作为节点，将每个节点的k个近邻与其进行有向连接。消息是有向边的向量，不同于其他GNNs的一点是，LUNAR中的聚合函数是一个可学习的聚合函数。

LUNAR不仅仅可以针对图数据进行建模，同时对于基于特征的结构化数据也可以建模。

模型设计

LUNAR在聚合时，并没有对k个近邻传来的信息采取统一的最大池化将其转化为一个最终信息，而是将这k个信息编码为一个k维的向量，并送入神经网络进行运算，从而通过神经网络的权重更新来实现聚合时的策略的可学习性。

由神经网络运算得到的聚合结果最终用于分类，0为正常样本，1为异常样本。由于训练集中的数据我们认为均是正常样本，因此需要一个合理的异常样本生成策略，使模型学到区分正负样本的分界线。

生成负样本

均匀分布

第一种方法是通过均匀分布生成负样本：
$${\text{x}}^{(negative)}\sim \mathcal{U}(-\epsilon ,1+\epsilon )\in {\mathbb{R}}^d$$
其中$\epsilon$是一个极小的正数，为了方便，原文中所有的实验$\epsilon$均设为0.1。训练数据标准化至的范围。由于异常样本可能距离正常样本距离过远导致模型难以学习到决策边界，因此需要生成一些更靠近正常样本的，分辨难度更高的异常样本。

子空间扰动

第二种方法，是在正常样本的所有特征维度中选取一个子空间，通过向子空间内的特征添加高斯噪声从而生成负样本：
$$\text{z}\sim \mathcal{N}(0,I)\in {\mathbb{R}}^d$$
$${\text{x}}_i^{(negative)}={\text{x}}_i^{(train)}+\text{M}\circ \epsilon \text{z}$$
其中$\epsilon$为一个极小的正整数，$\text{M}\in {\mathbb{R}}^d$是一个二进制随机变量构成的向量，$\text{M}$中的每个元素均有$p$的概率为1，$(1-p)$的概率为0。每个置为1的维度将会受到噪声干扰。原文的所有实验中，$p$均被设为0.3。

关键结果及结论

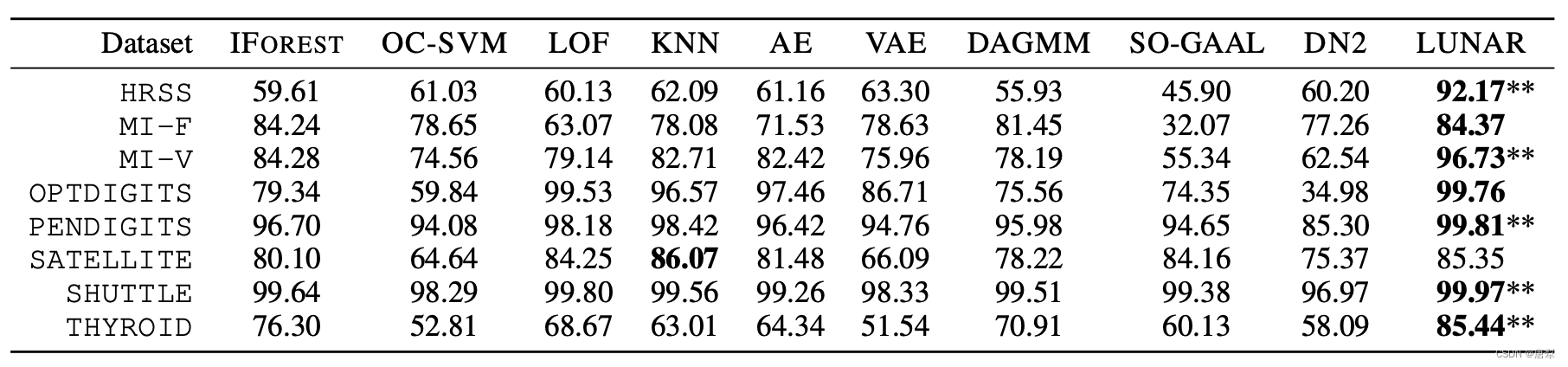
LUNAR在运算速度上明显快于其他深度模型，如HRSS数据集上，LUNAR耗时33.71秒，DAGMM则为55.92秒。这是因为LUNAR在训练时避免了直接训练高维输入特征，而是使用两点之间的距离。

和其他局部异常检测方法一样，LUNAR的思路还是寻找k近邻来解决问题。这在高维空间中，比如在处理图像数据时，很难保证距离是否有意义。

LUNAR的一大贡献在于，它成功统一了包括KNN，LOF，以及DBSCAN在内的局部异常检测方法。在统一框架下，基于其变换一致性，可以不同变换后的异常分。