本文主要是介绍《Enforcing geometric constraints of virtual normal for depth prediction》,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
《深度预测中虚拟法线的几何约束》
摘要
单目深度估计在理解三维场景几何中扮演了重要的角色。尽管最近的方法在评价指标方面取得了令人印象深刻的进展,如像素级的相对误差,但是大多数方法忽略了三维空间中的几何约束。在这项工作中,我们展示了高阶三维几何约束对深度估计的重要性。通过设计一个损失项确定一个简单的几何约束类型,即由重建的三维空间随机采样的三个点所确定的虚拟法线方向,我们可以极大地提高深度估计的准确率。值得注意的是,这种预测深度变得足够精确带来了一个好处,我们现在可以由深度直接恢复良好的场景的三维结构,例如点云和表面法线,消除了像以前一样训练新的子模型的必要性。在两个基准测试上进行了实验:NYU Depth-V2和KITTI表明了我们方法的有效性和先进性能。代码可以由以下网站获得:
1.简介
单目深度估计目的是从一副单目图像预测场景对象和相机之间的距离。对于理解三维场景来说这是一个十分重要的任务,例如识别三维对象和解析一个三维场景。
尽管单目深度估计是一个不适定的问题,因为许多三维场景能够投影到相同的二维图像中,但许多基于深度卷积神经网络(DCNN)的方法通过利用大量标记的数据取得了令人印象深刻的结果,从而利用标记数据的先验知识来解决模糊性。
这些方法通常将优化问题表示为点(point-wise)回归或者分类。也就是说,假设为独立同分布(i.i.d),总体损失是所有所有像素的损失的总和。为了提高性能,研究人员也努力使用除像素级(pixel-wise)项以外的其他约束。例如,使用连续的条件随机场(CRF)进行深度估计,将配对(pair-wise)的信息纳入考虑。其他高阶的几何关系也被采用,例如设计一个针对局部区域的重力约束或者在优化过程中加入深度到表面法线的相互转换。注意到,对于上述的方法来说,几乎所有的几何约束在场景中都是“局部”的,它们都是从二维或三维中的一个小的邻域中获得的。表面发现自然是“局部”的,因为它是由局部切平面定义的。由于大多数数据集的真实深度图像都是由消费级别的传感器(例如Kinect)获得的,深度值可能会有很大的波动。这种噪声的测量结果将不可避免地对这些局部约束地精度和有效性产生不利影响。更进一步,在小邻域上计算的局部约束不能充分使用场景几何的结构信息(这可能提高性能)。
为了处理这些局限性,在这我们从一个全局的视角提出了一个更加稳定的几何约束为深度预测考虑距离更大的邻域的关系,称之为虚拟法线。一些以前的方法已经在深度估计中使用了三维几何信息,几乎所有这些方法都聚焦于使用表面法线。相反地,我们是从估计的深度图中精确地重建三维点云。换句话来说,我们通过将二维图像中地RGB像素提升到与估计深度图中对应的三维坐标来生成三维场景。在这里三维点云是作为一个中间表示。有重建的点云后,我们可以使用许多类型的三维几何信息,不再局限于表面法线。这里我们通过随机采样三个距离较大的不共线的点,来考虑三维空间中较远距离两个像素的相关性(long-range dependency),以形成一个虚拟平面,其法线向量称之为虚拟法线(VN)。真实值和预测的VN之间的方向散度可以作为一个高阶的三维几何损失。由于点的较远距离的采样,深度测量中噪声造成的不利影响相比表面发现的计算大大减小,使得VN更加精确。此外,通过随机采样我们获得了大量的约束,对全局三维几何进行编码。第二,通过将估计的深度图从图像转换为三维点云表示,为将三维点云处理算法纳入二维图像和2.5维深度处理算法提供了更多可能性。在这里我们展示这种可能性的一个例子。
通过将高阶几何监督和像素级的深度监督结合起来,我们的网络不仅能够预测精确的深度图,还能够预测高质量的三维点云,以及其他几何信息,例如表面法线。值得注意的是,我们没有使用一个新模型或者引入网络分支来估计表面法线,而是直接从重建的点云中计算得到。图1的第二行显示了我们结果的一个例子。
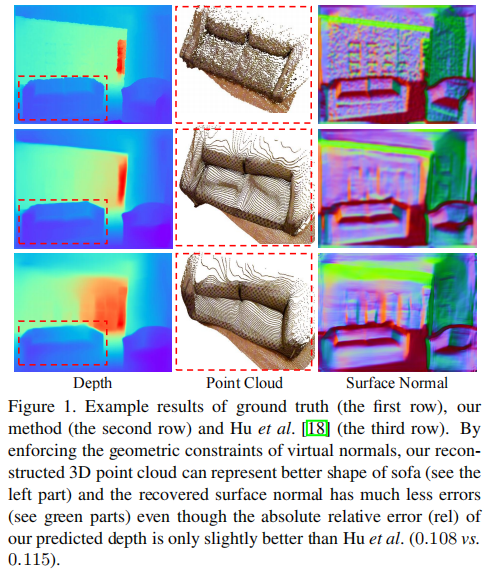
相比之下,尽管之前先进的方法能够以较小的误差预测深度,但是重建的点云结果与原形状相差很大。表面法线也包含很多错误。我们可能是第一个用单个网络达到高质量单目深度和表面法线预测的。
在NYUD-v2和KITTI数据集上的实验结果表明了我们的方法的先进性能。此外,在使用轻量化的网络骨架MobileNetV2训练时,我们的框架能够在网络参数和准确性之间提供一个更好的权衡。我们的方法在相当数量的网络参数下。比其他先进的实时系统性能高29%。此外,从重建的点云中我们能直接计算表面法线,其精度与基于特定DCNN的表面法线估计方法相同。
综上所述,这项工作中我们的主要贡献如下。
- 我们证明了在深度估计任务中,在三维空间中采用高阶几何约束的有效性。这种全局几何信息的实例化与一个简单有效的概念称之为虚拟法线(VN)。通过采用定义在VN上的一个损失,我们证明了三维几何信息在深度估计中的重要性,并设计了一个简单的损失项来使用它。
- 我们的方法可以重建高质量的三维场景点云,从中其他的三维几何特征也能够被计算,例如表面法线。在本质上,我们表明了人们不应该只考虑由深度表示的信息。相反,将深度转换为三维点云并使用三维几何可能对许多任务(包括深度估计)有所改善。
- 在NYUD-v2和KITTI上的实验结果表明我们的方法达到了先进的表现。
1.1Related Work
单目深度估计
从图像中进行深度预测是一个存在已久的问题。之前的工作能够氛围主动方法和被动方法。前者使用辅助光学信息进行预测,例如编码模式,与此同时,后者完全聚焦于图像内容。近期,单目深度估计已经被广泛研究。因为有限的几何信息能够直接从单目图像中进行提取,所以这本质上是一个不适定的问题。最近,由于超深卷积神经网络(如ResNet)得到的结构特征,各种基于DCNN的方法学习用深度CNN特征预测深度。Fu等人提出了一种编解码结构,能够从编码器中提取多尺度特征,并用一种端到端的方式进行训练,不需要迭代细化。他们的方法在一些数据集上达到了先进的性能。Jiao等人提出了一种注意力驱动的损失,其融入了语义先验来提高对不平衡分布数据集的预测准确率。
之前的大多数方法只能采用像素级的深度监督来训练网络。相比来说,Liu等人将连续条件随机场和DCNN合并起来,利用相邻像素的一致性信息。CRF为邻域建立起了一个成对的约束。此外,也研究了一些高阶的约束。Chen等人应用生成对抗训练使网络自动学习感知上下文和块级的损失。注意到,这些方法大多是直接使用深度,而不是在三维空间中工作。
表面法线
表面法线对于三维场景理解来说使一个重要的几何信息。一些数据驱动的方法已经达到了可靠的结果。Eigen等提出了一个有不同输出通道的CNN来直接预测深度图像,表面法线和语义标签。Bansal等提出了一个双线程网络来首先预测表面法线,然后进一步与输入图像一起学习姿态。注意到这些方法大多数将表面法线预测和深度估计预测作为多种不同的任务。
2.我们的方法
我们的方法解决了单目深度预测,同时从预测的深度重建高质量的三维点云。整个流程在图2中展示。
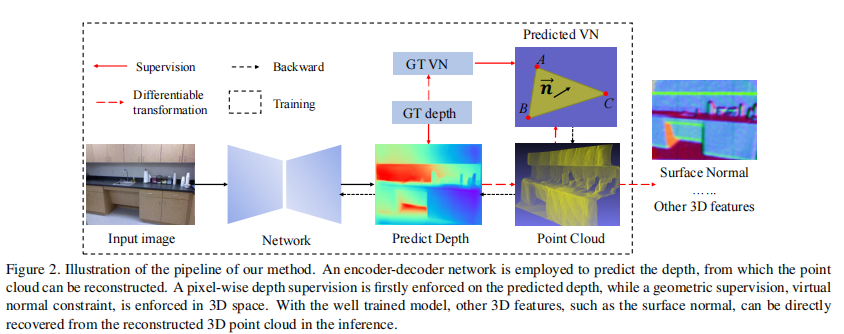
我们将一幅RGB图像作为一个编解码网络的输入图像并预测深度图
。从
中可以重建出三维场景点云
。真实点云
从真实深度图
重建。
我们使用两种监督来训练网络。我们首先跟随标准的单目深度估计方法,利用对
进行像素级深度监督。利用重建的点云,然后我们用提出的虚拟法线对齐
和
之间的空间关系。
当网络训练好时,我们不仅仅能获得精确地深度图,还有高质量的点云。从重建的点云,能够计算其他三维特征,例如表面法线。
2.1高阶几何约束
表面法线
表面法线对于许多基于点云的应用(例如配准和目标检测)来说是一个重要的“局部”特征。这是一个很有希望提高深度预测效果的三维线索。人们可以应用真实值和计算得到的法线之间的角差作为一个几何约束。这种方法的一个主要的问题是,当从一个深度图或者三维点云计算表面法线时,会对噪声很敏感。此外,表面法线仅仅考虑到了小范围内的局部信息。
我们根据[21]计算表面法线。其假设局部三维点都处于相同的平面,其法线向量就是表面法线。实际上真实深度图通常是由有限精度的消费级传感器采集的,所以深度图是被噪声污染的。由于噪声和局部采样块的大小,局部重建的点云会有很大变化。(图3(a))

我们在NYUD-V2数据集上实验测试表面法线计算的鲁棒性。 在目标像素周围使用了五个不同的采样尺寸来采样点,用来计算其表面法线。采样的区域是。计算得到的表面法线之间的均值差异误差(平均)呗估计。从图3(b),我们可以认识到对于不同的采样尺寸,表面法线非常不同。例如,3×3和11×11之间的平均表面法线是22°。这种不稳定的表面法线会对其学习的效果产生消极影响。同样的,其他表明”局部“相对关系的三维几何约束也会遇到这个问题。
虚拟法线
为了在三维空间中得到鲁棒的高阶几何监督,我们提出了虚拟法线(VN)在更大的范围内的区域之间建立三维几何联系。点云能够从基于针孔相机模型的深度进行重建。对于每一个像素,其世界坐标系下的三维位置
可以用透视投影得到。我们将相机坐标系设置为世界坐标系。然后三维坐标系
就能够表示为:

其中是深度,
和
分别是沿着
和
坐标轴的焦距。对应的三维点是
![]()
基于约束,集合中的三个点被限制不共线,
是两个向量之间的夹角。
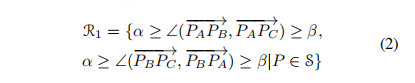
其中,和
是超参数 。在所有的实验中,我们设置
。
为了在三维空间中采样更大范围内有模糊相对位置的点,我们对![]() 中的每一个集合采用大范围约束
中的每一个集合采用大范围约束。
![]()
其中在我们的实验中。
因此,在每个集合中的三个三维点可以建立一个平面。我们通过计算平面的法线向量来编码
集合关系,其可以写作
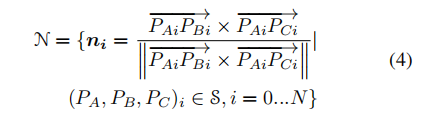
其中是虚拟平面
的法线向量。
对深度噪声的鲁棒性
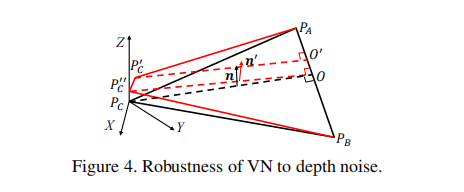
相比于局部表面向量,我们的虚拟法线对噪声更加鲁棒。在图4中,我们采集了三个远距离的三维点。假设和
位于
平面上,
在
轴上。当
变为
,虚拟法线的方向从
变为
。
是平面
和
轴的交点。因为
和
约束,
和
之间的不同通常非常小,其很容易展示:
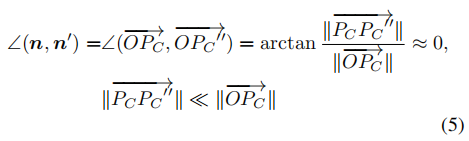
此外,我们进行了一项简单的实验来证明我们提出的虚拟法线对抗数据噪声的鲁棒性。我们构建了一个单位圆,然后添加高斯噪声来模拟理想的无噪声数据和真实噪声数据。如图5(a)。然后我们从含噪声的表面和理想表面采样100K个集合点来分别计算虚拟法线,同时也计算表面法线。对于高斯噪声,我们使用不同的方差来模拟不同的噪声等级,,均值为
。实验的结果展示在图15c。我们可以法线我们提出的虚拟法线相较于表面法线对数据噪声更加鲁棒。其他局部约束也对数据噪声敏感。
大多数“局部”集合约束,例如表面法线,事实上执行的是表面的一阶平滑度,对于深度图预测的帮助很小。相反的,提出的VN在三维空间中建立起了大范围的关系。相较于成对CRFs,VN编码基于三元组的关系,所以是高阶的。
虚拟法线损失
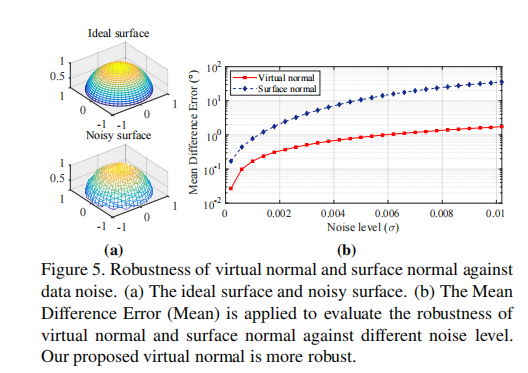
我们可以采样大量的三元组并计算相应的VNs。有了采样的VNs,我们可以计算散度作为虚拟法线(VNL)损失:
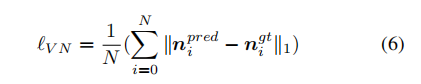
其中是满足
和
的有效的抽样组的数量。在实验中我们采用了在线的困难样本挖掘。
像素级深度监督
我们也使用了一个标准的像素级深度图损失。我们将真实深度值量化并将深度预测表示为一个分类问题,而不是回归问题,并使用交叉熵损失。特别地,我们遵循[2]使用加权的交叉熵损失(WCEL),权重是信息增益。阅读[2]来获取细节。
为了获得精确的深度图并恢复高质量的三维信息,我们将WCEL和VNL组合在一起来对网络输出进行监督。总体损失是:
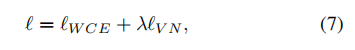
其中是是一个权重,在所有实验中设置为5,使两项的尺度大致相同。
注意到上述总体损失函数是可微的。的梯度能够很容易计算,因为公式4和6都是可微的。
3.实验
在这一节,我们进行了一些实验将我们的方法与先进的方法进行对比。我们在两个数据集上对我们的方法进行了评估,NYUD-V2和KITTI。
3.1数据集
NYUD-V2
NYUD-V2数据集由464个不同的室内场景组成,在后续被分为249个场景用于训练,215个用于测试。我们从训练集中随机采样了29K张图像来形成NYUD-Large。注意到DORN使用的是整个训练集,比我们使用的要大得多。除了整个数据集,官方还标注了1449张图像(NYUD-Small),其中795张图像用于训练,其他的用于测试。在消融实验中,我们使用NYUD-Small数据。
KITTI
KITTI数据集包括了超过93K张室外图像和深度图,分辨率在1240×374左右。所有的图像都是在行驶的汽车上用立体相机和雷达采集的。我们在Eigen等人分割的29个场景中的697张图像上进行测试,在888张图像上验证,并在剩余的32个场景中的23488张图像上训练。
3.2实施细节
在ImageNet上预先训练好的ResNeXt-101(32×4d)模型被用作我们的骨干模型。在梯度下降法中应用了一个多项式衰减方法,基本学习率为0.0001,幂次为0.9。权重衰减和动量分别被设置为0.0005和0.9。在我们的实验中Batch size为8。模型在NYUD-Large和KITTI上训练10个epochs,在消融实验中,在NYUD-Small上训练40个epochs。我们通过下列方法在训练样本上进行数据增强。对于NYUD-V2,RGB图像和深度图用比例[1,0.92,0.86,0.8,0.75,0.7,0.67]随机改变尺寸,在水平方向上随机翻转,最终随机裁剪为尺寸为384×384的NYHUD-V2图像。相似的流程也应用在KITTI上,但是改变尺寸的比例为[1,1.1,1.2,1.3,1.4,1.5],且被裁剪为384×512。注意到深度图也应用对应的调整比例缩放。
3.3评价指标
我们遵循之前的方法[24],基于以下指标定量评价单目深度估计的性能:平均绝对相对误差(rel),平均误差(
),均方根误差(rms),均方根对数误差(rms(log))和阈值下的精度(
![]() )。
)。
3.4与先进方法的对比
在这一节,我们详细的比较了我们的方法和先进方法。
NYUD-V2
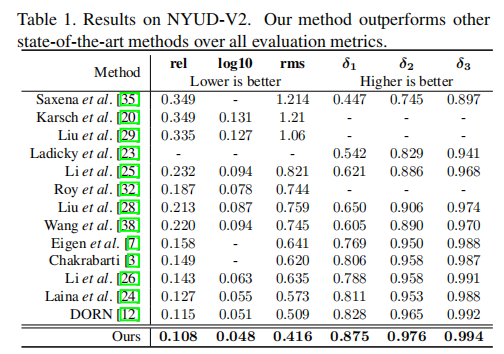
在这个实验中,我们在NYUD-V2数据集上与其他先进方法进行比较。表1展示了我们提出的方法在所有评价指标上都比其他先进方法性能更好。相较于DORN,我们在所有评价指标上将准确率提高了0.2%-18%。
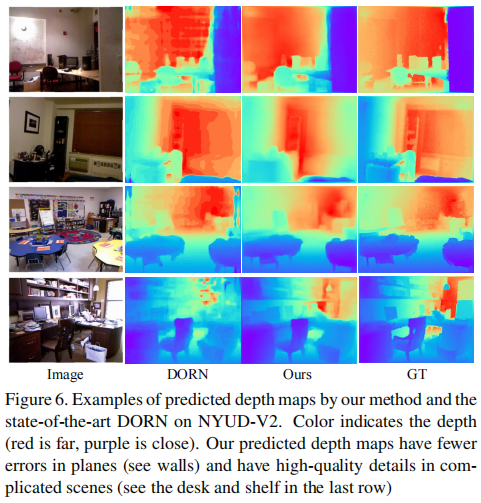
除了量化的比较,我们也在图6中展示了一些我们的方法和先进的DORN之间的可视化结果。可以清楚的看到,所提出的方法预测的深度更加精确。我们的平面更加平滑,并有更少错误(观察红色的墙壁区域没在第一二三行)。此外,图6的最后一行表示在复杂场景中我们预测的深度更加精确。我们在架子和桌子区域有更小的误差。
KITTI
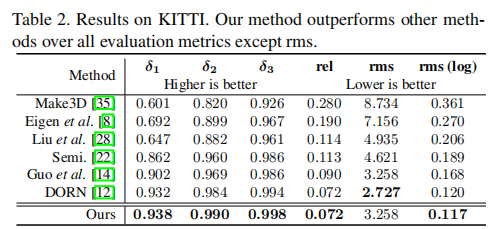
为了表面我们提出的方法在室外场景下也能够达到先进水平,我们在KITTI数据集上测试我们的方法,表2中的结果表示我们的方法在所有评价指标(除了均方根误差)上都比其他方法性能更好。均方根误差仅仅比DORN落后一点。注意到对于室外场景,均方根对数误差通常是人们感兴趣的指标,而不是均方根误差,在这一点上我们的更好。
3.5消融实验
在这一节中,我们进行了一些消融实验来分析我们方法的细节。
VNL的有效性
在这个实验中,为了证明提出的VNL的有效性,我们将其与两种像素级的深度图监督进行比较,一个是成对的几何监督,一个是高阶的集合监督:1)普通的交叉熵损失(CEL);2)损失(
);3)表面法线损失(SNL);4)成对几何损失(PL)。我们从深度图中重建点云并从点云中恢复表面法线。真实值和恢复的表面法线之间的角差定义为表面法线损失,是三维空间中的一个高阶几何监督。承兑损失是三维中两个向量之间的方向差异,是在真实值和预测的点云中随机采样的成对的点。PL的损失函数如下,
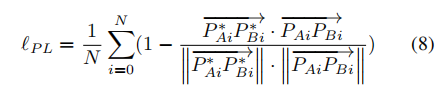
其中![]() 和
和![]() 是从真实点云和预测点云中分别采样得到的成对的点。
是从真实点云和预测点云中分别采样得到的成对的点。是成对点的总数量。
我们也对成对点使用了大范围约束,所以,与VNL类似,PL也能够视为是三维空间中的全局几何监督。其实验结果展示在表3。WCEL是后续所有实验的基线。
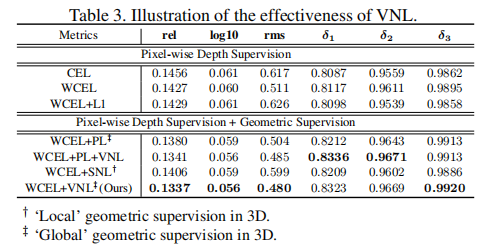
首先,我们分析了像素级深度监督对预测性能的影响。因为WCE在CE损失中使用了权重,所以其性能稍好于CE损失。然而,当我们在深度图上采用两个像素级监督(WCEL+L1)时,性能不再有提高。所以使用两个像素级的损失项没有帮助。
其次,我们分析了补充的三维几何约束(PL,SNL,VNL)的有效性。与基线(WCEL)进行比较,三种补充的三维几何约束能够不同程度地提高网络性能。我们提出的VNL与WCEL相结合具有最好的性能,将基线性能提高了8%。
第三,我们分析了三种几何约束之间的不同。由于SNL只能够应用均匀的局部区域的几何关系,所以其性能在所有评价指标上是三种约束中最差的。相较于SNL,因为PL约束时全局几何关系,其性能明显更好。然而,WCEL+PL的性能不如我们提出的WCEL+VNL的性能好。当我们进一步将我们的VNL添加到WCEL+PL上,精确度会有少许提升,与WCEL+VNL相当。所以,尽管PL是三维空间中的一个全局几何约束,成对的约束不能够像我们提出的VNL一样对更好的几何信息进行编码。
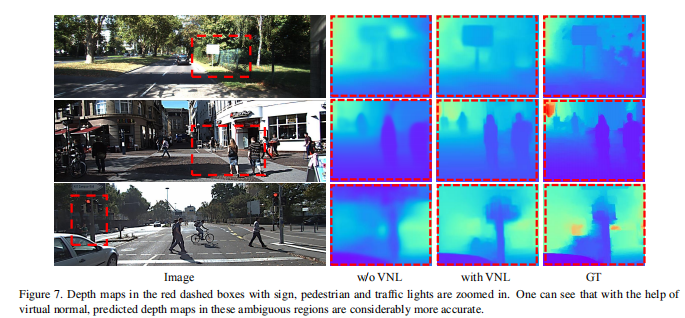
最后,为了进一步显示VNL的有效性,我们分析了在KITTI数据集上进行网络训练时有无VNL监督的结果。可视化的对比结果在图7中进行了展示。可以看出VNL能够在模糊区域能够提高网络的性能。例如,标志(第一行),远处的行人(第二行)和图中最后一行的红绿灯能够表面所提出的VNL的有效性。
综上所述,在三维空间中的几何约束能够显著增强网络的性能。而且三维空间中全局和高阶约束比局部和成对的约束具有更强的监督。
采样数量的影响
前面我们已经证明了VNL的有效性。在这里讨论样本大小对VNL的影响。物品,我们采样了六组不同尺寸的点集合,0K,20K,40K,60K和80K及100K来建立VNL。0K表示模型不用VNL监督进行训练。采用rel进行评估。图8显示,20K点组建立VNL的rel下降了5.6%。然而,当样本数量从20K到100K时,rel仅仅下降了一点。所以,当样本达到一定数量时,样本的多样性足以构建全局几何约束,使样本性能饱和。
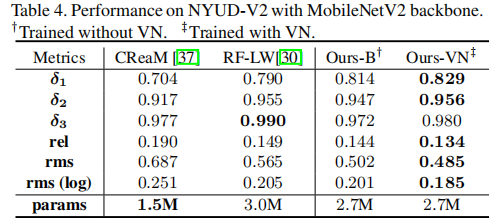
轻量级骨干网络
我们在轻量网络上用MobileNetV2骨干网络来训练网络,以评估提出的几何约束的有效性。我们在NYUD-Large上训练10个epochs。表4中的结果表示提出的VNL可以提高1%-8%的性能。相比于之前先进的方法,我们在所有评价指标上将准确率提高了约29%,在参数和准确率上达到了更好的平衡。
3.6从估计的深度中恢复三维特征
我们已经讨论了,有了三维空间中的几何约束,网络能够得到更加精确的深度和获取更高质量的三维信息。在这里我们展示了恢复的三维点云和表面法线来支持这一点。
三维点云
首先,我们比较我们预测的深度重建的三维点云和DORN重建的三维点云。图9显示了我们的整体质量比他们的有显著的提升。尽管我们预测的深度在评价指标上之比他们稍好一点,但是我们重建得到的墙(见图9的第二行)更加平整且误差更小。床的形状也与真实值更接近。从鸟瞰视角,很难区分他们结果的床的形状。图1中的点云也能得到相似的结论。

表面法线
最后,我们比较了计算出的表面法线和先前先进方法得到的表面法线,并在表5中显示了量化的结果。真实值如[7]所述。我们首先将几何计算的结果和基于DCNN的优化方法进行比较。尽管我们没有优化一个子模型来得到表面法线,但我们的结果优于大多数以前的方法,甚至在30°指标上是最好的。
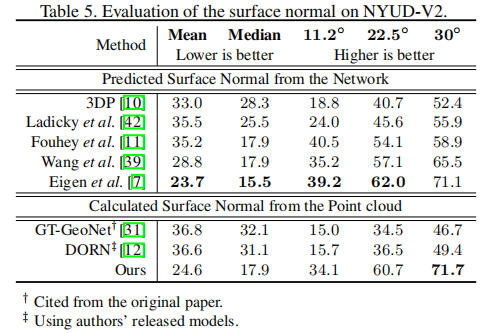
此外,我们将从重建点云直接计算得到的表面法线和DORN和GeoNet得到的进行比较。注意到我们运行已发布的DORN代码和模型来得到深度图,然后从深度图中计算表面法线,而GeoNet的评价指标则引自原论文。在表5中,我们可以看出,在高阶几何监督下,我们的方法的性能大大优于DORN和GeoNet,甚至于直接训练输出法线的特征方法相近。这表明我们的方法可以引导模型从图像中学习形状。
除了量化的比较,图10所显示的可视化的影响表明我们直接计算表面法线的方法不仅仅在平面(第一行)上精确,在复杂的曲面区域上也有更高的质量(第二和最后一行)。

4.总结
在这篇论文中,我们提出了在三维空间中构建一个大范围的几何约束VNL用于单目深度预测。相比于之前在二维空间中仅有像素级深度监督的方法,我们的方法不仅能够获得精确的深度图,也能够恢复高质量的三维特征,例如点云和表面法线,消除了优化一个新的子模型的必要性。相比于其他三维约束,我们提出的VNL对噪声更加鲁棒,能够编码更强的全局约束。在NYUD-V2和KITTI上的实验已经证明了我们的方法的有效性和先进的性能。
特别的,为了证明我们的方法能够生成合理的局部形状,直接从我们方法估计的深度中导出的法线要优于许多近期的深度估计方法,并和那些训练输出法线的方法接近。我们希望我们的方法能够提供一个有用的工具,并刺激洞察力,不仅预测深度,而且从单目图像中预测形状。
5.附录
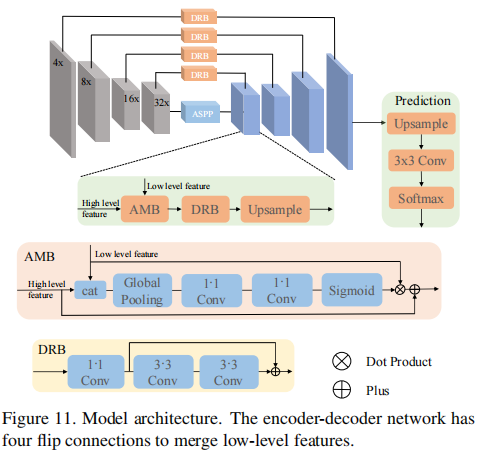
5.1模型
我们模型的一个总体框架如图11所示。网络主要包括两个部分,一个编码器用于从中在不同的尺度建立特征,一个解码器用于重建深度图。受[27]启发,该解码器有几个自适应融合块(AMB)组成,以融合不同尺度的特征,并通过扩张残差块(DRB)来转换特征。为了增强解码器的感受野,我们设置DRB中所有3×3卷积的扩张率为2,并在编码器和解码器之间插入一个空洞空间金字塔(ASPP)模块(扩张率:2,4,8)。此外,我们从不同级别的编码块中建立4个翻转连接来融合更多低级的特征。AMB将会学习融合的参数进行自适应融合。除了最高级别512个通道的特征,其他翻转的特征维度是256。最后,一个预测模块,一个3×3卷积和一个softmax被用于将特征维度从256个通道转换到150深度箱。
在轻量化骨干网络实验中,骨干网络用MobileNetV2网络替代。为了进一步减少参数,四个翻转连接的维度减小到(128,64,64,64)。在预测模块中,特征从64个通道转换到60个深度箱。
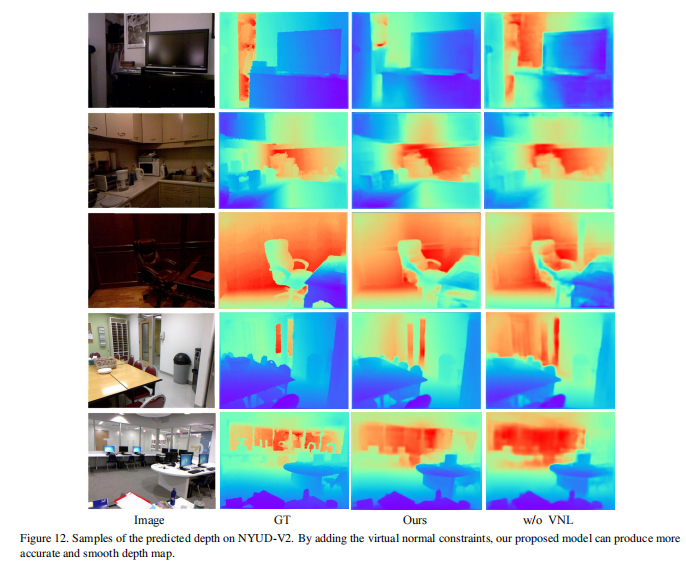
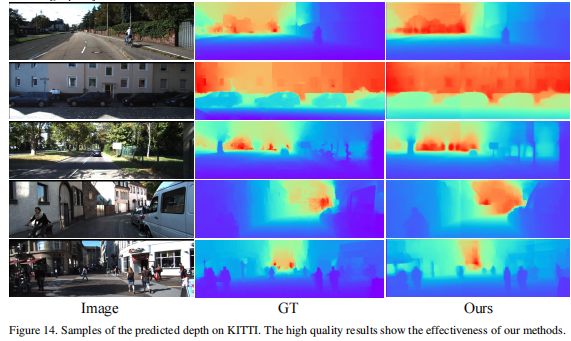
5.2预测的深度和表面法线
我们提供了更多在KITTI和NYUD-V2数据集上预测的深度图和恢复的表面法线。深度图在图12和14中展示,恢复的表面法线在图13中展示。

5.3三维点云
为了进一步展示从预测的深度中重建的三维点云的质量,我们从NYUD-V2和KITTI的测试部分选择了三个场景。随机选择了三个视角来展示重建点云,结果在图15和16中进行了展示。


这篇关于《Enforcing geometric constraints of virtual normal for depth prediction》的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








