LK光流法---金字塔改进

LK光流法注意事项

LK光流法有三个假设条件：

1. 亮度恒定：一个像素点随着时间的变化，其亮度值（像素灰度值）是恒定不变的。这是光流法的基本设定。所有光流法都必须满足。
2. 小运动： 时间的变化不会引起位置的剧烈变化。这样才能利用相邻帧之间的位置变化引起的灰度值变化，去求取灰度对位置的偏导数。所有光流法必须满足。
3. 空间一致：即前一帧中相邻像素点在后一帧中也是相邻的。这是LK光流法独有的假定。因为为了求取x,y方向的速度，需要建立多个方程联立求解。而空间一致假设就可以利用邻域n个像素点来建立n个方程。

LK金字塔光流法

虽然光流法假设2本身并不容易满足，在实际应用中容易遇到间隔帧出现较大变化的情况，从而对计算结果造成较大的误差。为了减缓这一假设不成立情况所导致的问题，可以在计算中缩小图像的尺寸，从而使得像素点的运动减少（图像尺寸减半时，像素运动自然也同时减半）。
具体的假设当图像为400×400时，物体速度为[16 16],那么图像缩小为200×200时，速度变为[8,8]。缩小为100*100时，速度减少到[4,4]。所以在源图像缩放了很多以后，原算法又变得适用了。所以光流可以通过生成原图像的金字塔图像，逐层求解，不断精确来求得。简单来说上层金字塔（低分辨率）中的一个像素可以代表下层的两个。
在实际应用过程中：在大多数的情况下，超过4的金字塔图像层次没有太大的意义。

建立金字塔

用高斯函数对图像进行滤波，显然这是一个低通滤波，得到的图像就是一个模糊的图像。对模糊的图像进行降采样（图像宽高变为原来的一半，只取图像的偶数行和偶数列），那么就得到了金字塔的一层图像。重复高斯模糊-降采样，就可以依次得到一组图像从G0, G1, G2, G3…这就是金字塔的建立过程。
具体的使用下面低通滤波器对当前图像卷积
$$\left[\begin{array}{ccc}\frac{1}{16}& \frac{1}{8}& \frac{1}{16}\\ \frac{1}{8}& \frac{1}{4}& \frac{1}{8}\\ \frac{1}{16}& \frac{1}{8}& \frac{1}{16}\end{array}\right]$$
之后去掉奇数行和奇数列，只留下偶数行和偶数列即得到上一层图像

金字塔迭代

总体来讲，金字塔特征跟踪算法描述如下：首先，光流和仿射变换矩阵在最高一层的图像上计算出；将上一层的计算结果作为初始值传递给下一层图像，这一层的图像在这个初始值的基础上，计算这一层的光流和仿射变化矩阵；再将这一层的光流和仿射矩阵作为初始值传递给下一层图像，直到传递给最后一层，即原始图像层，这一层计算出来的光流和仿射变换矩阵作为最后的光流和仿射变换矩阵的结果。

根据上一层$L+1$计算的结果推算出的当前层的初始光流量为：
$$g^L=(g_x^L,g_y^L)$$
在当前L层实际要计算的残余光流量为：
$$d^L=(d_x^L,d_y^L)$$
重新定义误差函数为：
$$\epsilon =\Sigma \Sigma (I(x,y)-I(x+g_x^L+d_x^L,y+g_y^L+d_y^L){)}^2$$

这里其实可以发现，在$g^L$的作用下，搜素范围跳出了原来的小窗，搜素范围实际上是扩大了的

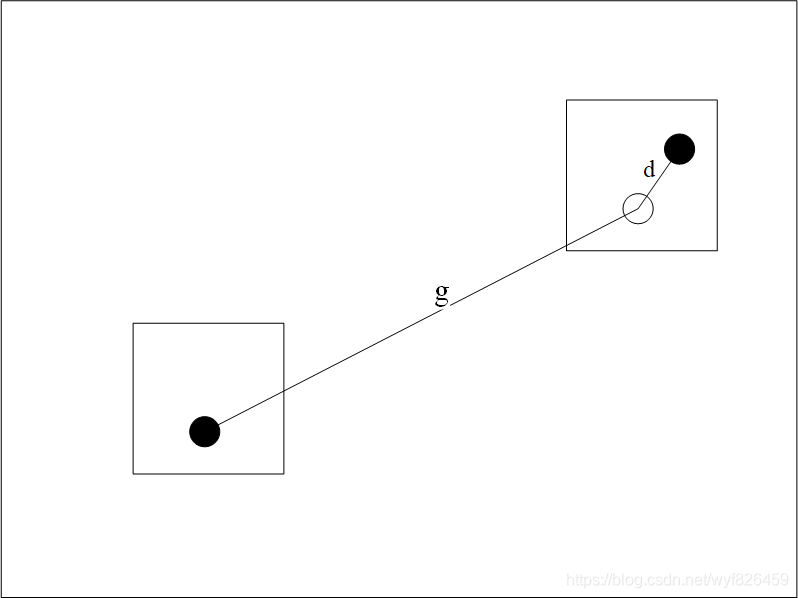
另一方面通过上一层计算出较大的g值，剩下的小范围的d在小范围搜素即可得到,具体的在下一节进行搜索

迭代过程：得到g和d后下一层的g的计算方式如下：
$$g^{L-1}=2(g^L+d^L)$$

对于这个迭代过程的初始值设置为
$$g^{Lm}=[00{]}^T$$

可以看到两点：

1. 观察递归过程可以发现$$d=\sum _{L=0}^{L=L_m}{2}^L{d}^L$$
2. 光流量的搜索范围大幅提高，量化一下：$$d_{maxfinal}=(2^{L_m+1}-1)d_{max}$$
   

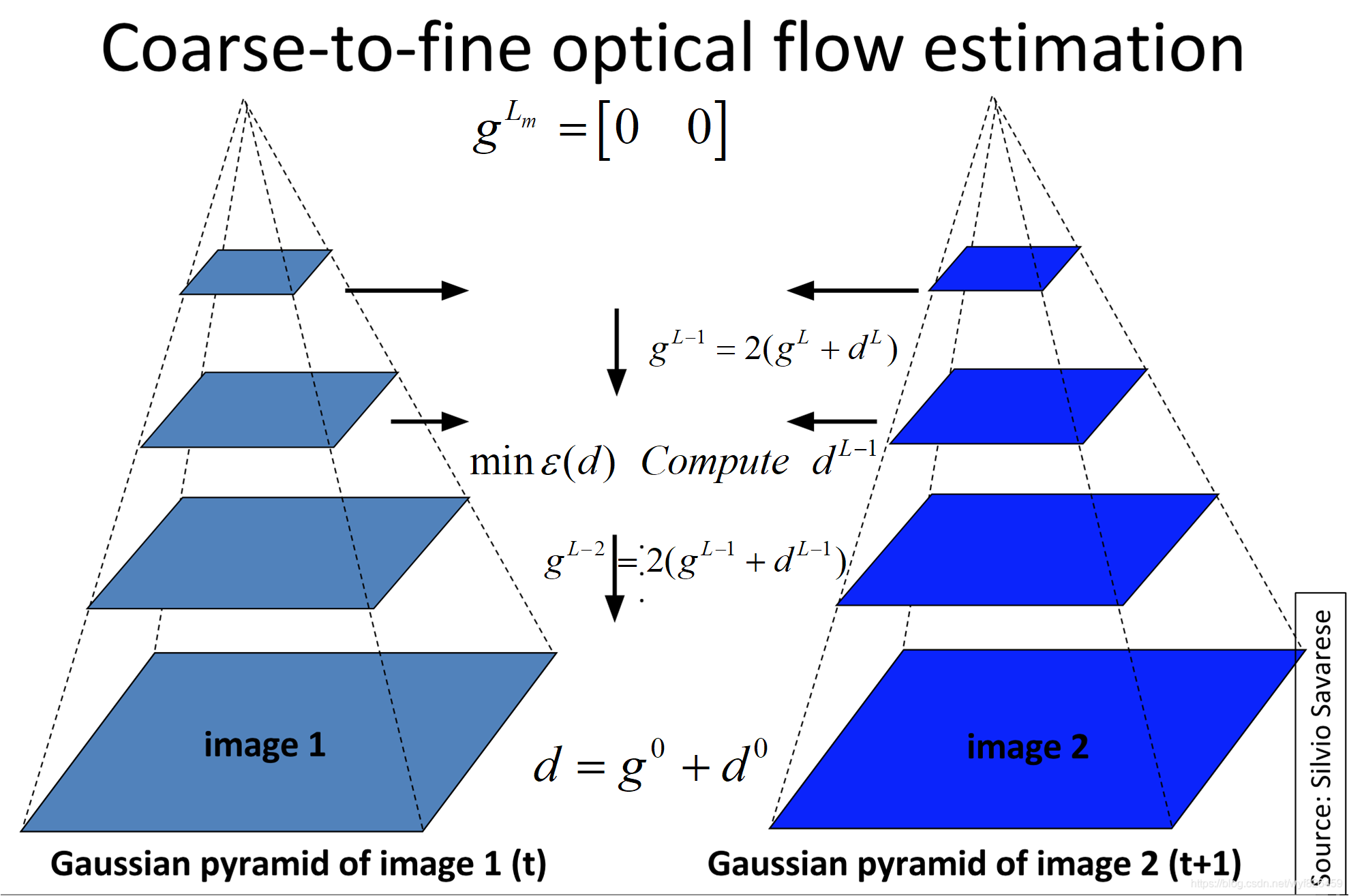
如何计算残余光流量

首先利用上一层计算出的$g^L$，将问题简化，等效成两幅图像A，B
$$A(x,y)\doteq I^L(x,y)$$

$$B(x,y)\doteq J^L(x+g^L,y+g^L)$$

问题变成最小化下面误差：

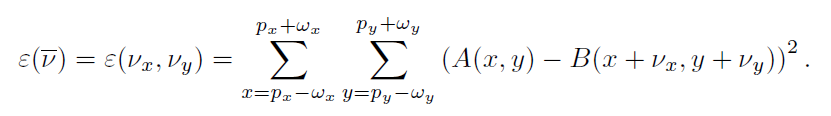
优化此目标函数是为了求解$\vec{v}$,求解最小值应该在函数的驻点处，所以对该函数进行求导

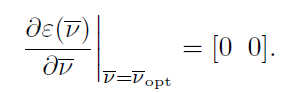
即：

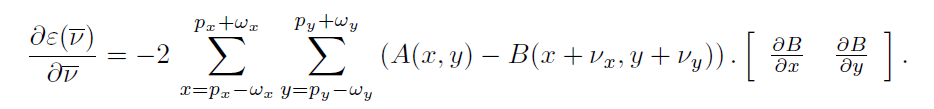
把其中B在点$P(x,y)$附近泰勒展开:

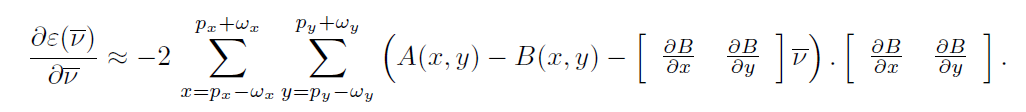
这里笔者认为论文中将A-B作为I的导数然后利用算子求解的方式误差稍大，尝试直接化简上面的泰勒展开式为:
$$\frac{1}{2}\frac{\partial ϵ(\vec{v})}{\partial (\vec{v})}=\Sigma \Sigma (\left[\begin{array}{cc}\frac{\partial B}{\partial x}\frac{\partial B}{\partial x}& \frac{\partial B}{\partial y}\frac{\partial B}{\partial x}\\ \frac{\partial B}{\partial x}\frac{\partial B}{\partial y}& \frac{\partial B}{\partial y}\frac{\partial B}{\partial y}\end{array}\right]\left[\begin{array}{c}{v}_x\\ v_y\end{array}\right]-\left[\begin{array}{c}(A-B)\frac{\partial B}{\partial x}\\ (A-B)\frac{\partial B}{\partial y}\end{array}\right])$$
这里把论文中的原方法放到此处：核心思想在于用A的差分来代替B的导数

下面的方法又和论文相同，类似得可以得：
$$G\doteq \Sigma \Sigma \left[\begin{array}{cc}\frac{\partial B}{\partial x}\frac{\partial B}{\partial x}& \frac{\partial B}{\partial y}\frac{\partial B}{\partial x}\\ \frac{\partial B}{\partial x}\frac{\partial B}{\partial y}& \frac{\partial B}{\partial y}\frac{\partial B}{\partial y}\end{array}\right],\vec{b}=\Sigma \Sigma \left[\begin{array}{c}(A-B)\frac{\partial B}{\partial x}\\ (A-B)\frac{\partial B}{\partial y}\end{array}\right]$$

于是:

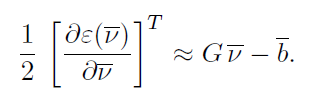
驻点为0，进而
：
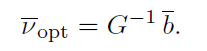于是残余光流量得解

牛顿迭代法

在上一次计算出LK光流后，将得到的光流vkvk用来更新参考图像的像素位置（平移），之后再次计算光流。重新更新$v_x,v_y$。如此循环直到迭代次数达到上限或者误差量$\epsilon$小于设定的阈值时停止。 按照上述情况来看，停止迭代后，A图和B图两张图在(x,y)(x,y)点处像素完全重合的。这里要说明得是利用论文中的方法，在此次迭代过程中，G是不变的，而利用上文中的方法，G是变化的

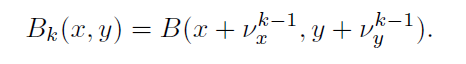
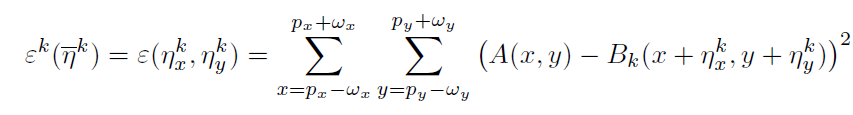
加入仿射变换

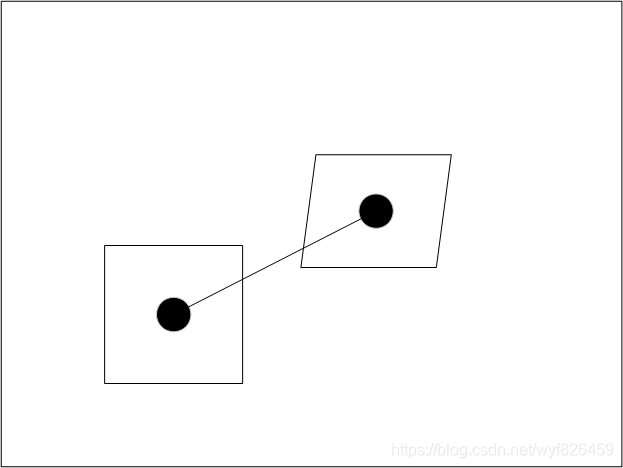
光流法的思路是找一个点$u$对应的点$u+d$，发现单纯使用一个点$u$发现约束不够，于是认为$u$附近的点和$u$的特性相同，那么就变成了一个矩形窗口的点对应一个矩形窗口的点；加入仿射变换后，就是认为这一个矩形窗口的点从$I$图变换到$J$图是有仿射变换的，于是就变成了一个平行四边形。这样可以进一步提高精度。

$$ϵ(d,A)=\sum _{x=-w_x}^{w_x}\sum _{y=-w_y}^{w_y}(I(x+u)-J(Ax+d+u){)}^2$$
其中A：
$$A=\left[\begin{array}{cc}1+d_{xx}& d_{xy}\\ d_{yx}& 1+d_{yy}\end{array}\right]$$

参考资料

https://blog.csdn.net/zhonghuan1992/article/details/38508185
https://blog.csdn.net/qq_35368183/article/details/86601807
https://www.jianshu.com/p/e3570a9216a6
https://blog.csdn.net/App_12062011/article/details/51880258
https://blog.csdn.net/gh_home/article/details/51502933
高翔—《视觉SLAM十四讲》
论文原文：Bouguet J Y. Pyramidal Implementation of the Lucas Kanade Feature Tracker Description of the algorithm http://robots.stanford.edu/cs223b04/algo_tracking.pdf
加入仿射的论文:Bouguet J Y. Pyramidal implementation of the affine lucas kanade feature tracker description of the algorithm[J].https://pdfs.semanticscholar.org/aa97/2b40c0f8e20b07e02d1fd320bc7ebadfdfc7.pdf